기초수학 등차 수열

1. 수열

수열은 규칙성을 가지고 나열되어 있는 수들을 말한다.

---

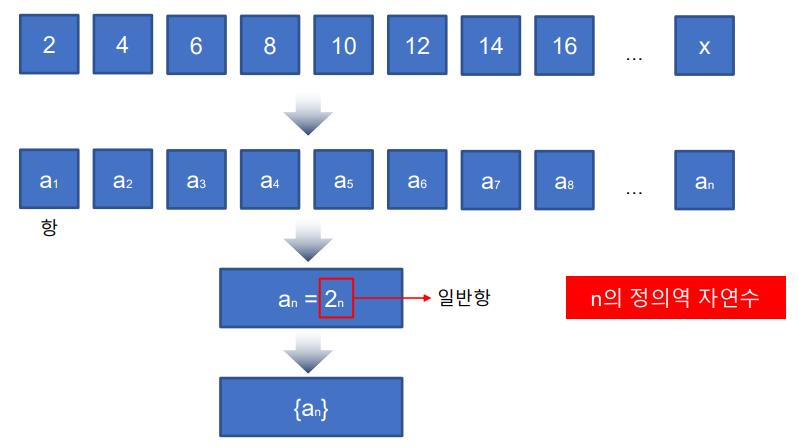
2씩 증가하기에 등차 수열이라고 한다.

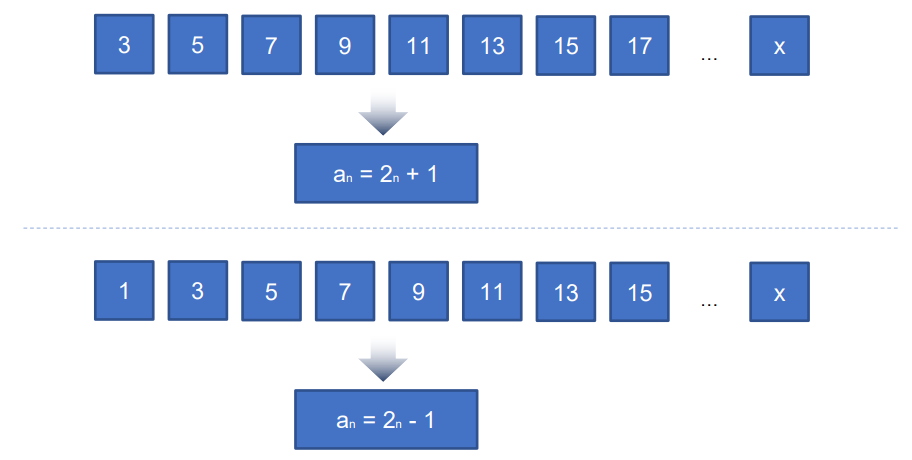
1.1 항들의 합과 항의 관계

• 특정항은 특정항까지의 합에서 특정항 이전의 항까지의 합과 같다.

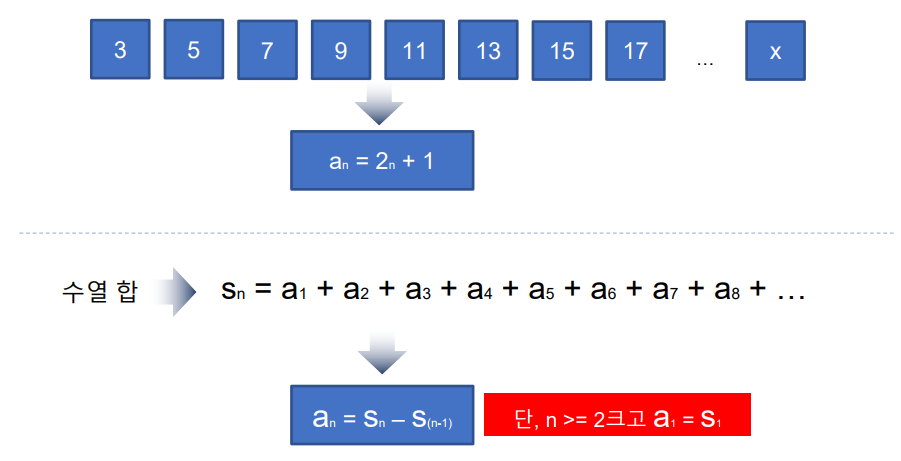
• 수혈 합은 모든 항들을 더한거를 말한다.

2. 등차 수열

등차 수열은 연석된 두항의 차이가 일정한 수열이다.

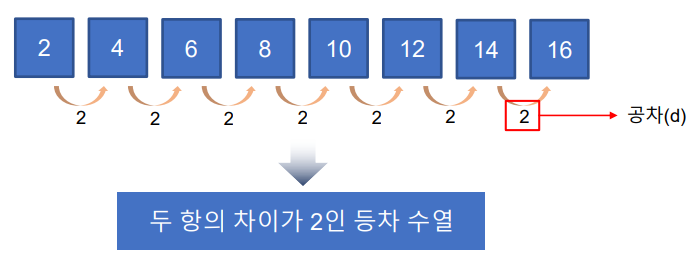
공차(d)는 차이가 나는 수를 뜻한다.

위의 예시에서 2씩 차이가 나기 때문에 공차는 2다.

2.1 등차 수열과 일반항

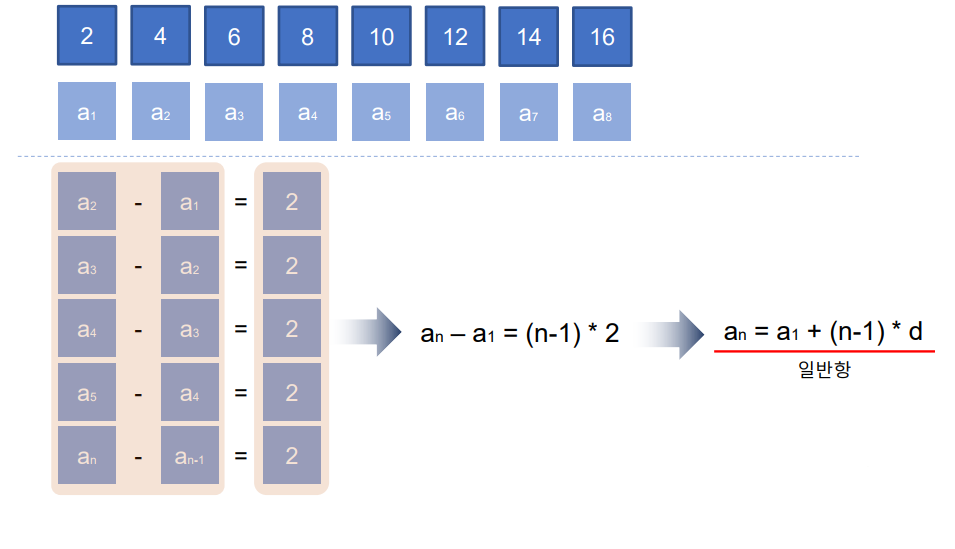
위의 예시에서 알 수 있는 공차는 a1 + (n-1)*d다.

첫번째 항이 2일 때:
2+(n-1)*2 = 2 + 2n -2 = 2n

결과적으로 해당 등차 수열의 일반항은 2n이다.

2.2 등차 중항

등차 중항은 연속된 세 항에서 가운데 항을 뜻한다.

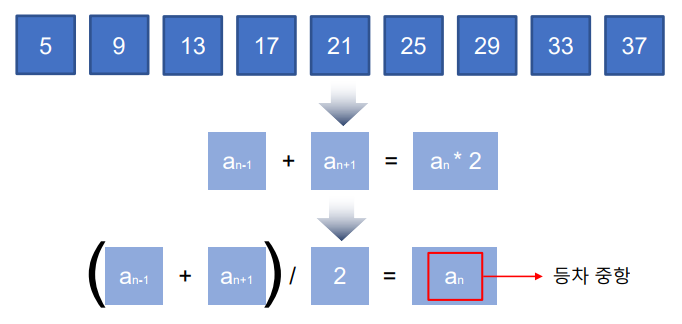
2.3 등차 수열의 합

규칙성을 이용하여 모든 항들의 총합을 구할 수 있다.

Sn = 8(2+16)/2 = 72 # 8은 모든 항의 수

3. Python을 이용한 등차 수열

3.1 등차 수열

Example 1: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an = {2, 5, 8, 11, 14, 17, 20, 23, 26, 29, ...}

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0 # n번째 항의 값
n = 1
while n <= inputN:

    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값: {}'.format(n, valueN))
        n += 1
        continue

    valueN += inputD
    print('{}번째 항의 값: {}'.format(n, valueN))
    n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))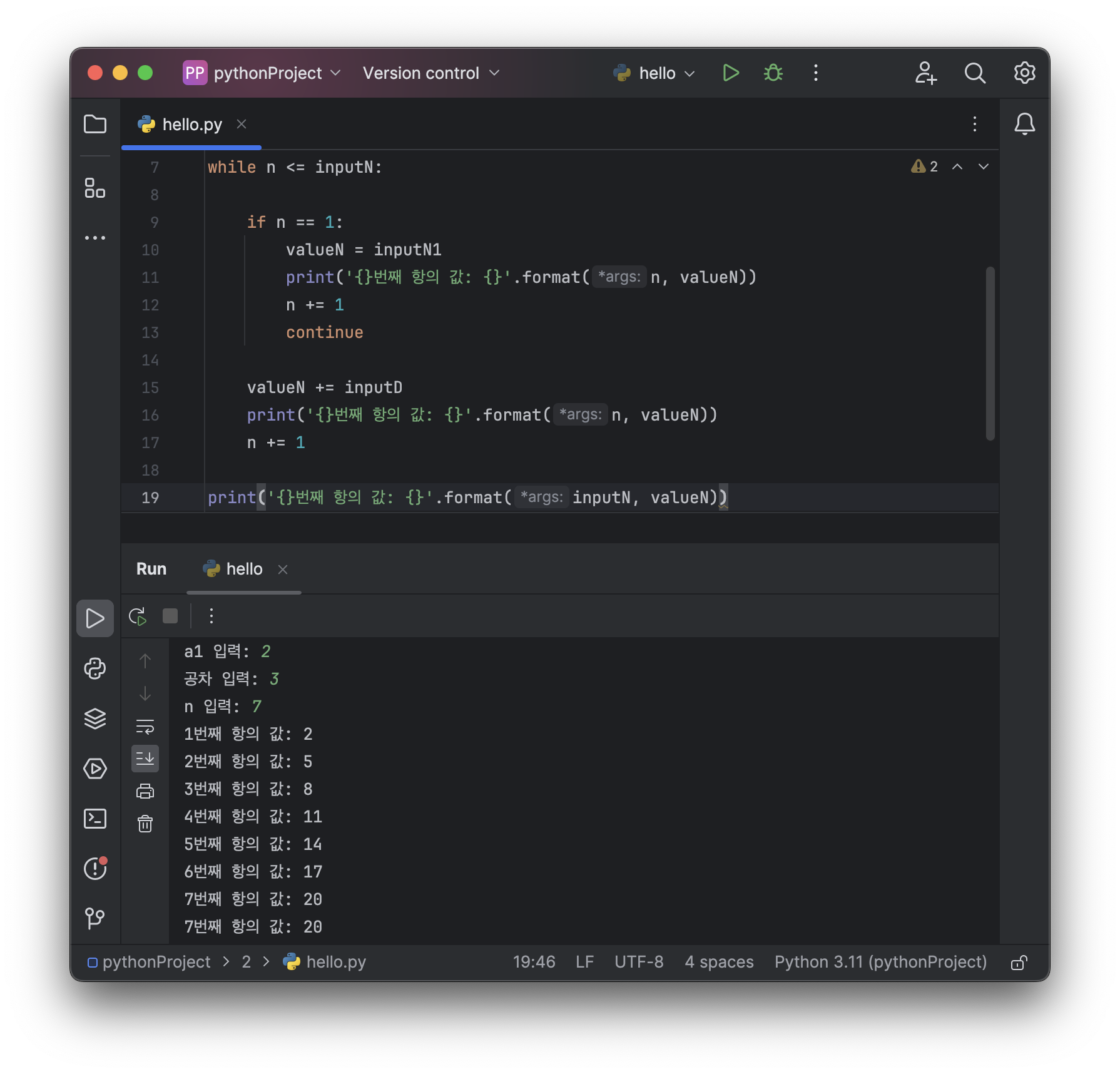

Example 2: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an = {2, 5, 8, 11, 14, 17, 20, 23, 26, 29, ...}

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0

# 등차 수열(일반항) 공식: an = a1 + (n-1) * d
valueN = inputN1 + (inputN - 1) * inputD
print('{}번째 항의 값: {}'.format(inputN, valueN))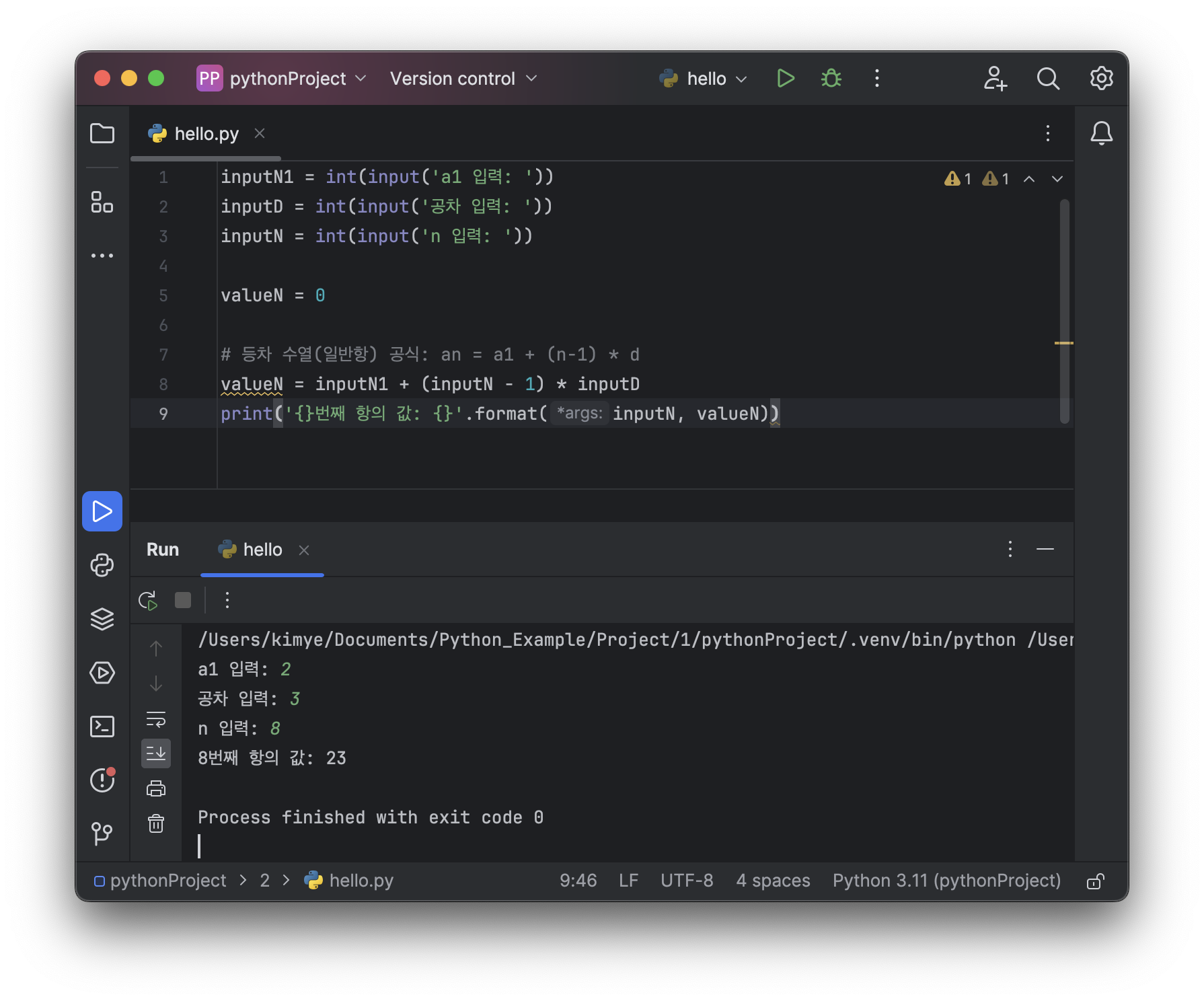

3.2 등차 수열의 합

Example 1: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an = {5, 9, 13, 17, 21, 25, 29, 33, ...}

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1
while n <= inputN:

    if n == 1:
        valueN = inputN1
        sumN += valueN
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue

    valueN += inputD
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1

print('{}번째 항까지의 합: {}'.format(inputN, sumN))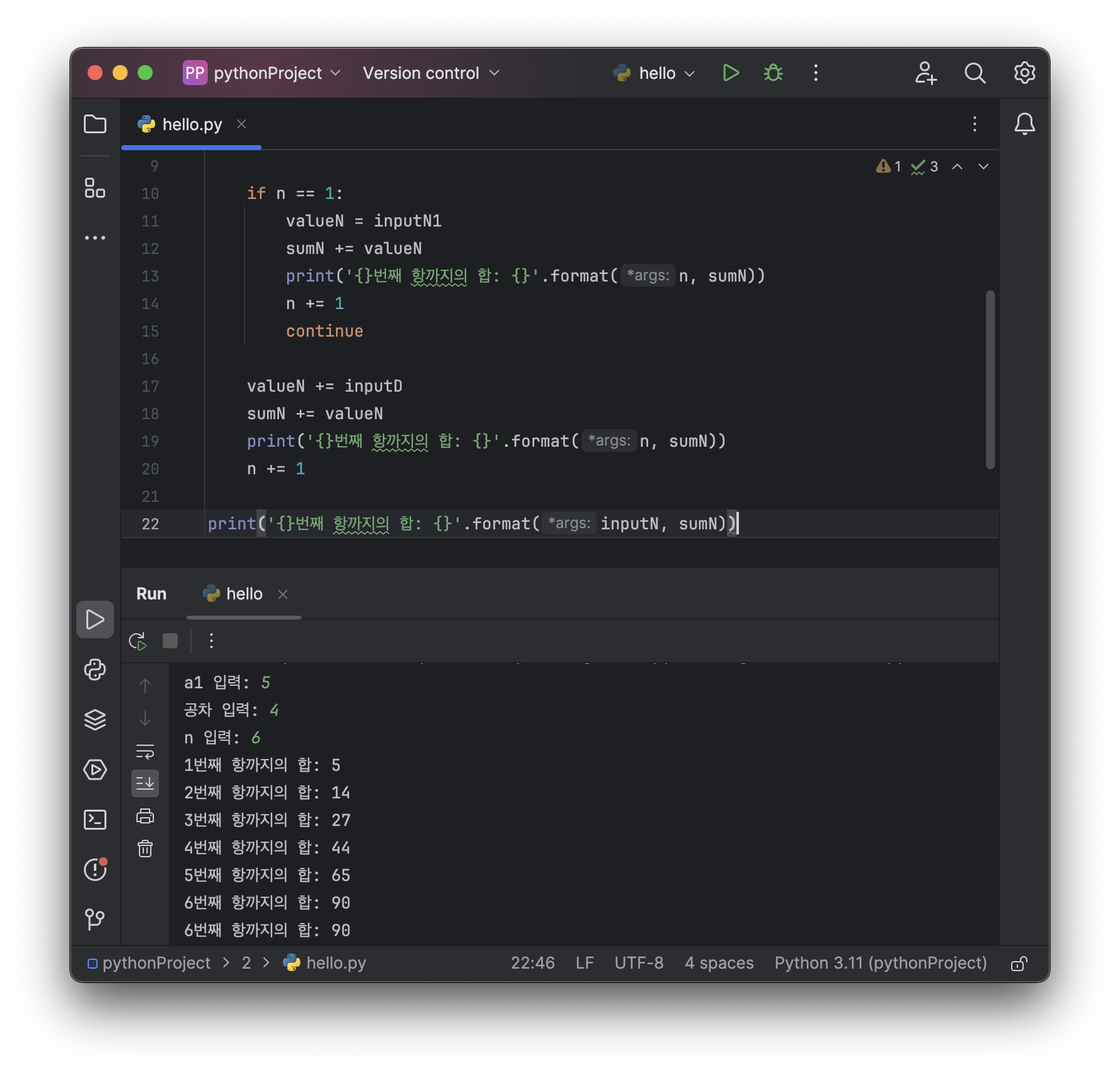

Example 2: 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램 만들기

an = {5, 9, 13, 17, 21, 25, 29, 33, ...}

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0

# 등차 수열(일반항) 공식: an = a1 + (n-1) * d
# 등차 수열(합) 공식: sn = n(a1 + an) / 2

valueN = inputN1 + (inputN - 1) * inputD
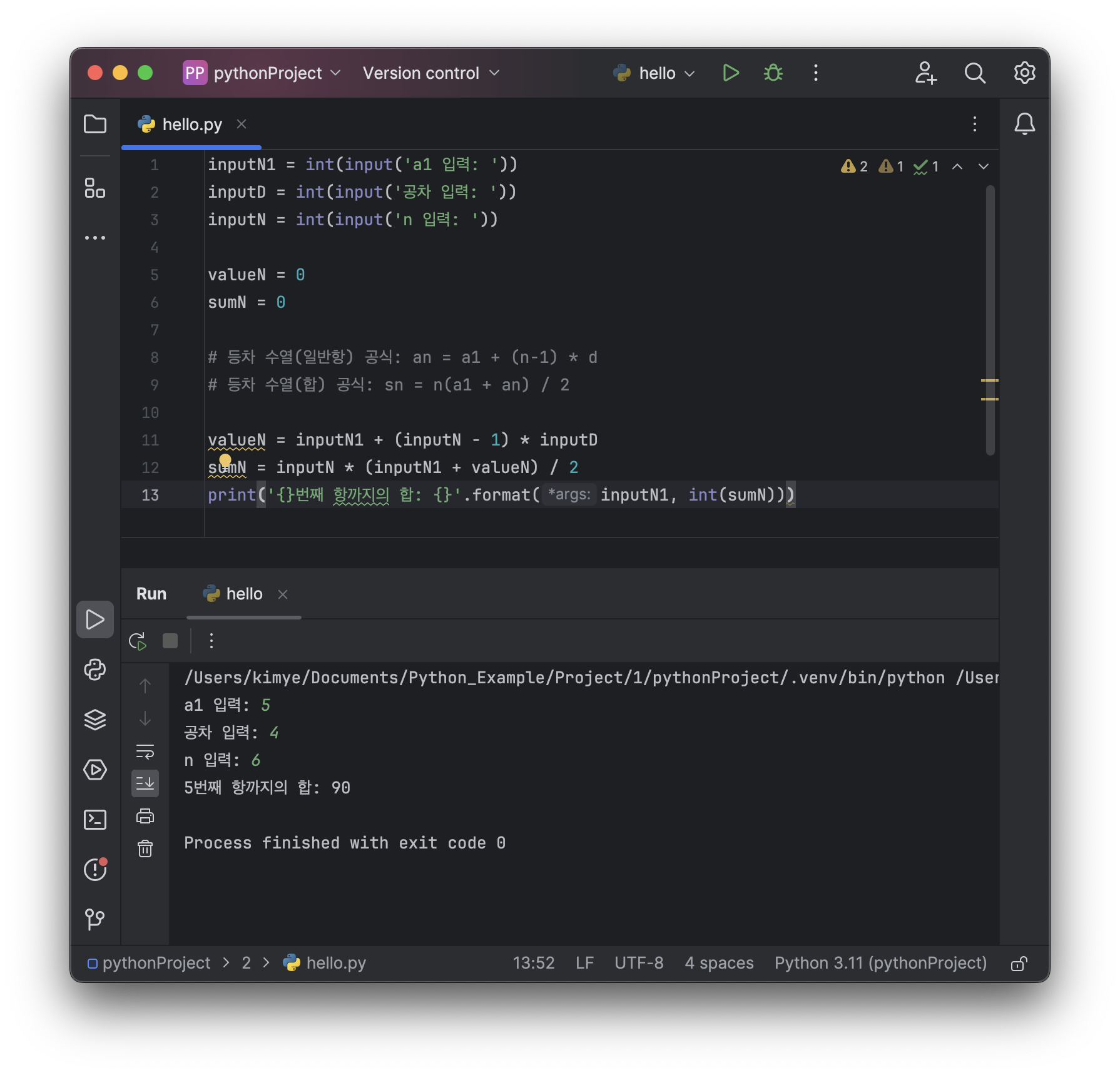
sumN = inputN * (inputN1 + valueN) / 2
print('{}번째 항까지의 합: {}'.format(inputN1, int(sumN)))