기초수학 최대공약수

1. 공약수

공약수는 두 개 이상의 수에서 공통된 약수이다.

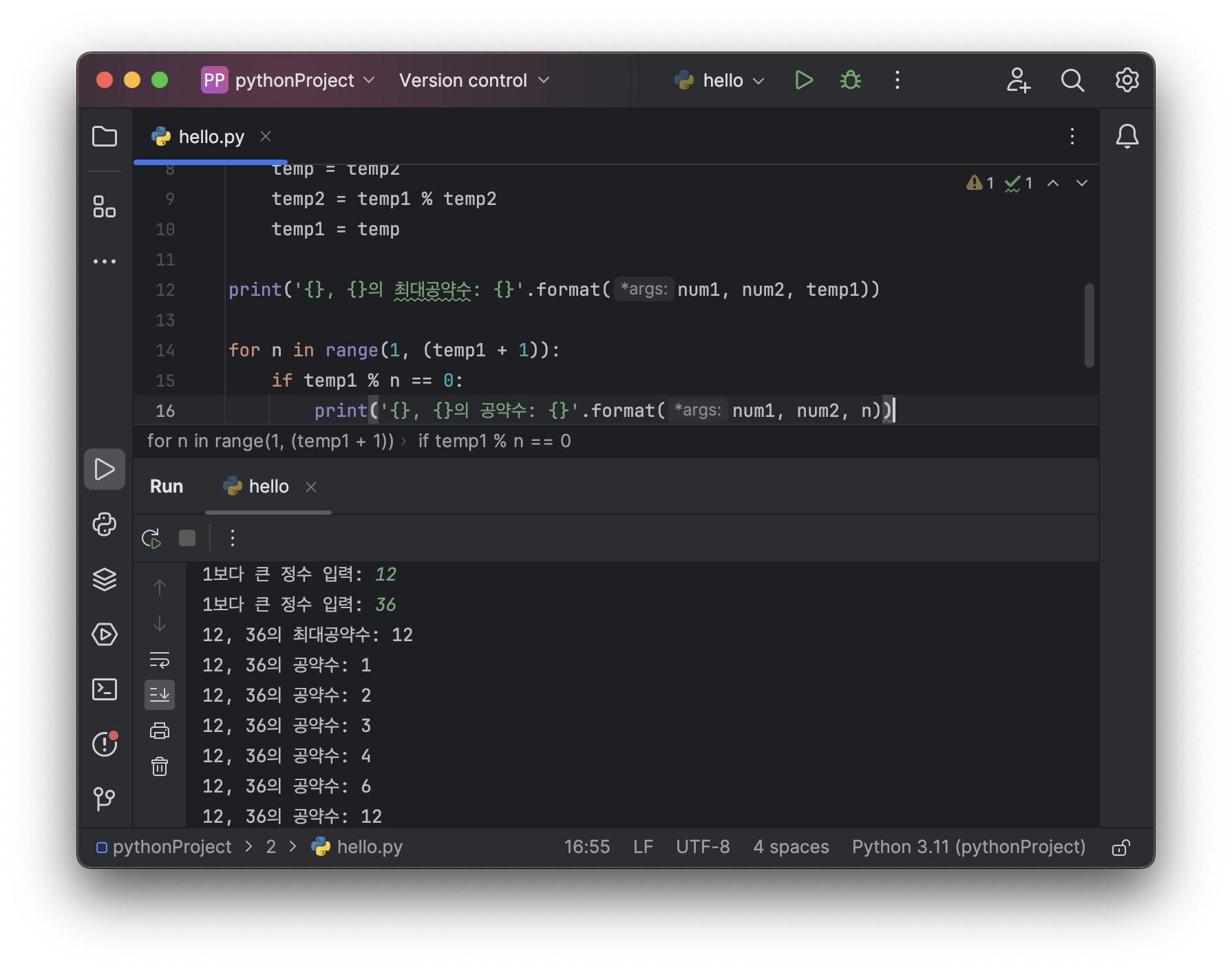
12의 약수: (1, 2, 3, 4, 6, 12)

20의 약수: (1, 2, 4, 5, 10, 20)

12와 20의 공약수: (1, 2, 4)

Example 1: 36, 60의 공약수

36의 약수: (1, 2, 3, 6, 12, 36)

60의 약수: (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60)

36과 60의 공약수: (1, 2, 3, 6, 12)

Example 2: 12, 52, 82의 공약수

12의 약수: (1, 2, 3, 4, 6, 12)

52의 약수: (1, 2, 4, 13, 26, 52)

82의 약수: (1, 2, 41, 81)

12, 52와 82의 공약수: (1, 2)

2. 최대공약수

최대공약수는 공통된 약수 중에서 가장 큰 수이다.

12의 약수: (1, 2, 3, 4, 6, 12)

20의 약수: (1, 2, 4, 5, 10, 20)

12와 20의 공약수: (1, 2, 4)

12와 20의 최대공약수: (4)

• 소인수분해를 이용하면 최대공약수 및 공약수를 구할 수 있다.

12의 소인수분해: 2^2 x 3

20의 소인수분해: 2^2 x 5

12와 20의 최대공약수: 2^2 = (4) # 공통인 소인수의 거듭제곱에서 지수가 작은 수를 모두 곱한다.

12와 20의 공약수(=4의 약수): (1, 2, 4)

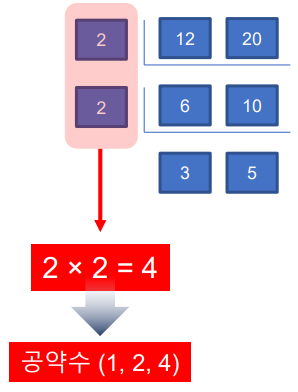
Example 1: 36, 60의 최대공약수

36의 소인수분해: 2^2 x 3^2

60의 소인수분해: 2^2 x 3 x 5

36과 60의 최대공약수: 2^2 x 3 = (12)

36과 60의 공약수(4의 약수): (1, 2, 4)

Example 2: 12, 52, 82의 최대공약수

12의 소인수분해: 2^2 x 3

52의 소인수분해: 2^2 x 13

82의 소인수분해: 2 x 41

12, 52와 82의 최대공약수: 2

• 좀 더 편리하게 최대공약수 구하는 방법: 소수로 나눗셈

12와 20의 최대공약수:

36와 60의 최대공약수:

3. 유클리드 호제법

유클리드 호제법을 이용해서 최대공약수를 구할 수 있다.

x, y의 최대공약수는 y, r(x%y)의 최대공약수와 같다.

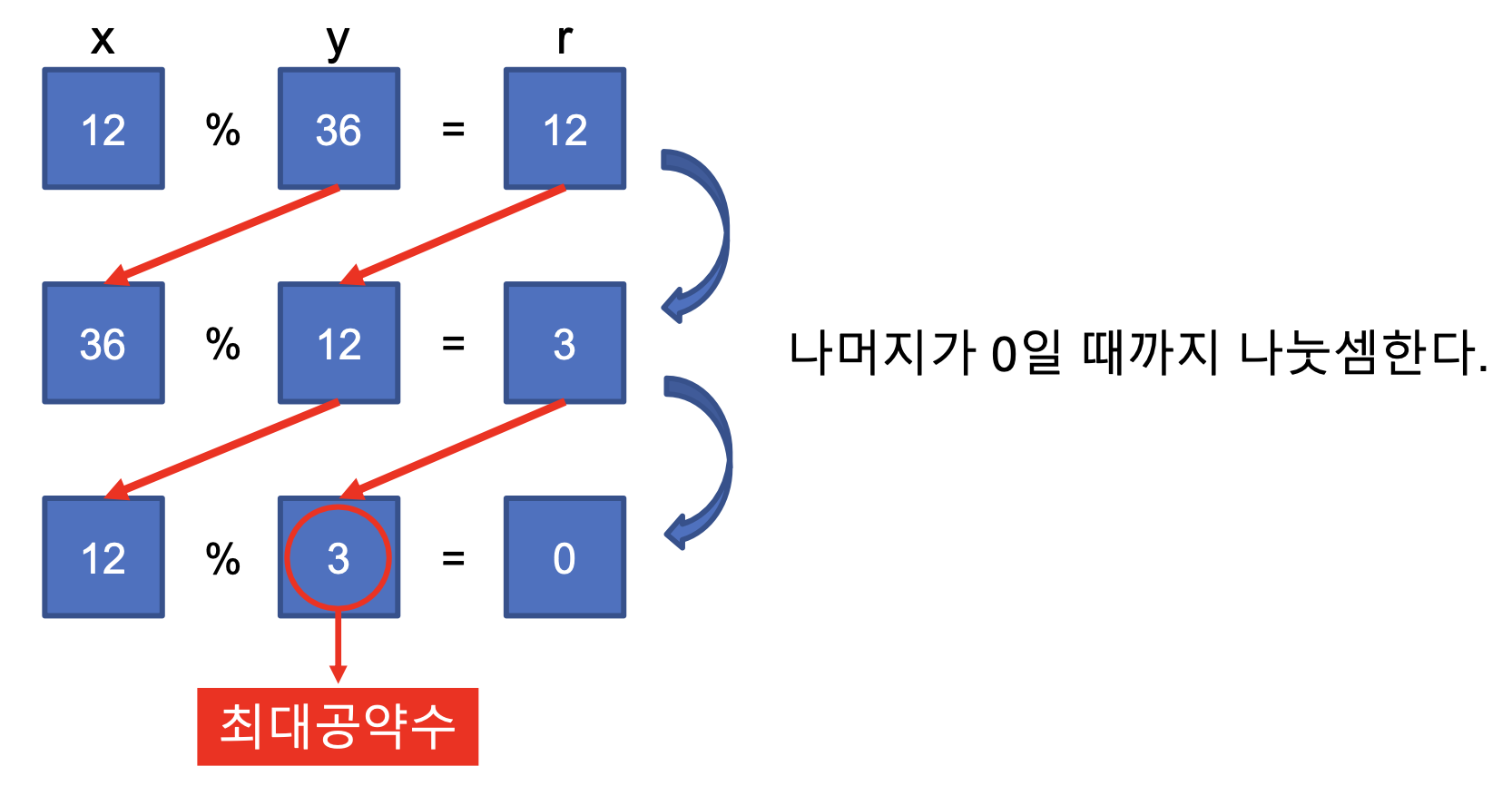
위와 같이 유클리드 호제법을 이용해서 12(x)와 36(y)의 최대공약수는 3이라는걸 구할 수 있다.

temp1 = num1
temp2 = num2

while temp2 > 0:
    temp = temp2
    temp2 = temp1 % temp2
    temp1 = temp

print('{}, {}의 최대공약수: {}'.format(num1, num2, temp1))

for n in range(1, (temp1 + 1)):
    if temp1 % n == 0:
        print('{}, {}의 공약수: {}'.format(num1, num2, n))