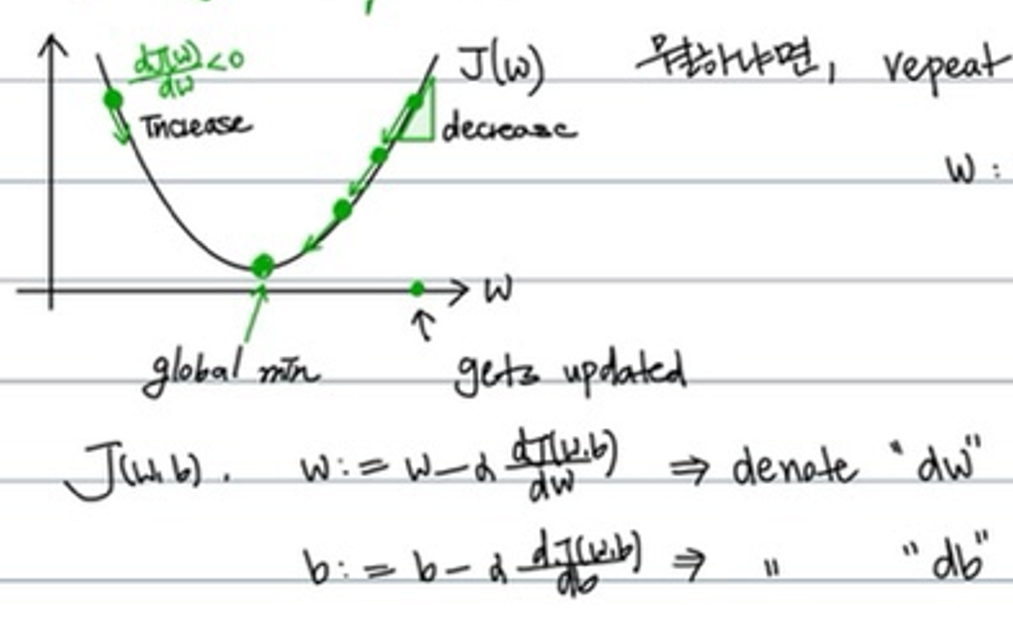
global min값에 도달하는 parameter w의 값을 찾기 위해서 learning_rate*dw값을 조금씩 빼 주는 이유는 무엇일까? 우리는 cost function을 알고 있어서 바로 구할 수 있는데도 말이다.
위의 곡선과 같이 convex형태의 cost function이거나, 입력값의 차원이 낮다면 우리는 아마 cost function을 통해서 쉽게 global optimum의 값을 구할 수 있을 것이다.
그러나 만약에 cost function이 엄청 복잡하다면? 그 함수를 특정 미분식으로 나타내기도 벅찰 것이다.
sanghyukchun님의 블로그에서 아래와 같은 내용을 확인할 수 있다.
Machine learning 문제를 풀다보면 이렇게 optimization을 해야하는 일이 아주 빈번하게 발생하는데, 안타깝게도 항상 이런 function들의 optimum point를 찾을 수 있는 것은 아니다. 가장 간단하게 생각했을 때 이런 point를 찾는 방법은 미분을 하고 그 값이 0이 되는 지점을 찾는 것인데, 안타깝게도 미분 자체가 되지 않는 함수가 존재할 수도 있으며, 미분값이 0이라고 해서 반드시 극점인 것은 아니기 때문이다. (saddle point를 생각해보자.) 따라서 대부분의 경우에 이런 방법으로 극점을 구하는 것은 불가능하며, 매우매우 특수한 일부 경우에 대해서 완전한 optimum을 찾는 것이 알려져 있다. 그리고 그 경우가 바로 convex optimization이다.
따라서 우리는 컴퓨터에게 특정한 learning_rate의 값을 지정하고, 그 보폭에 맞춰 조금씩 미분값을 빼 나아가 최적값을 찾는 방법밖에 없다.
