백준 10868

<최솟값 찾기 2>

난이도 : 골드 1

1. 백준 문제
   10868

2. 코드 알고리즘

• 세그먼트 트리
  세그먼트 트리

• 10868

  기존의 세그먼트 트리 알고리즘을 그대로 사용하고, 구간 최소를 구하는 함수에 대한 아이디어만 내면 된다.
  start index와 end index는 각각 좁히되 이전 시행의 min값과 비교해 나가면 된다.

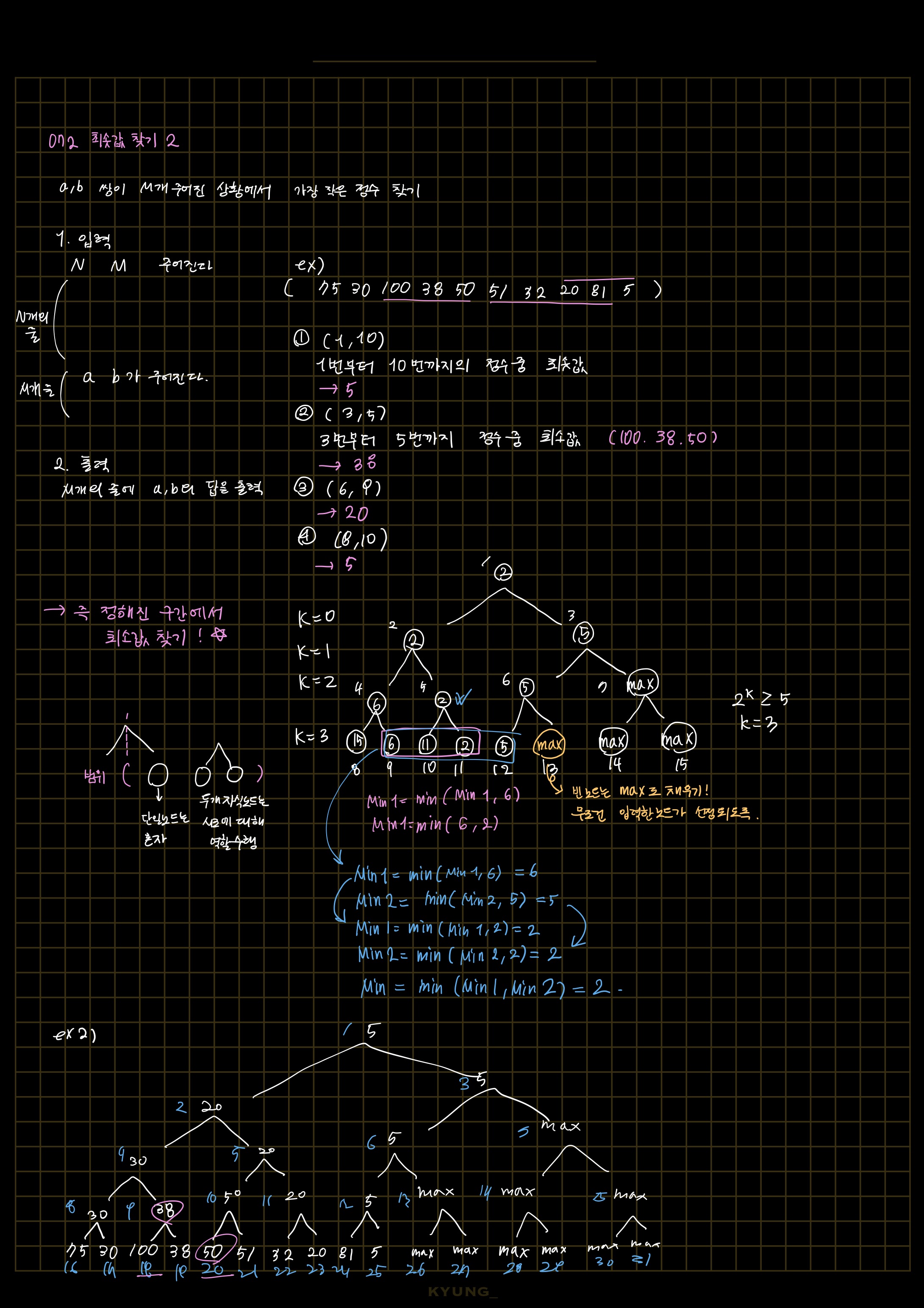
2-1. 슈도 코드

10868 슈도코드

n m 입력받기

tree_size 구하기
tree_hight 구하기
left_nodestart 구하기
tree 리스트 선언하기(sys.max로 선언하기)

n줄동안 tree 입력받기(left_nodestart 인덱스부터 입력받기)

toTreeIndex 함수 :
	while 인덱스가 1이 아니라면: #구간합과 다르게 2개씩 묶여서 시행됨
		부모노드에 min(왼쪽자식, 오른쪽자식) 넣기#(index-1, index) 
		# 맨끝 인덱스부터 시행됨 
		인덱스 2씩 감소 (쌍으로 진행됨)

#tree 리스트 완성하기
toTreeIndex(start 노드*2 - 1) #인덱스로 입력해주기
#입력받는 값은 맨 끝 인덱스

MIN1, MIN2 에 max 대입
def partialMin(start, end): #구간에서 최솟값찾기
	Min1, Min2 전역변수 선언
	while start <= end: #정해진 구간에서 양옆에서 시행하기(같아지면 안됨)
		start index 라면(오른쪽 노드라면):
			MIN1 = min(Min1, tree[start_index])
			start index에 1씩 더하기
		end index라면 (왼쪽 노드라면):
			min2 = min(Min2, tree[end_index])
			end index에 1씩 빼기
		start index//2
		end index//2
	return min(MIN1, MIN2)

m 줄동안 a, b 입력받기:
	partialMin(a,b) 실행 결과 출력

3. 코드

#10868
#https://www.acmicpc.net/problem/10868

import sys
import math
input = sys.stdin.readline

N, M = map(int, input().split())

tree_size = math.ceil(math.log2(N))
tree_hight = tree_size+1
left_NodeStart = 2**(tree_size)
max = sys.maxsize
tree = [max]*(left_NodeStart*2)

for i in range(left_NodeStart,left_NodeStart+N):
    tree[i] = int(input())

#tree 리스트 완성하기
def toTreeIndex(index):
    while index > 0:
        tree[index//2] = min(tree[index-1], tree[index])
        index -= 2

toTreeIndex(left_NodeStart*2-1)

def partialMin(start_index, end_index):
    #구간에서 최솟값 찾기
    global min1, min2
    while start_index <= end_index:
        if (start_index % 2) == 1:
            #print("min1, start_index", min1, tree[start_index])
            min1 = min(min1, tree[start_index])
            start_index += 1
        if (end_index % 2) == 0:
            #print("min2, end_index", min2, tree[end_index])
            min2 = min(min2, tree[end_index])
            end_index -= 1
        start_index = start_index//2
        end_index = end_index//2
    #print("min1, min2", min1, min2)
    return min(min1, min2)

for i in range(M):
    min1 = max
    min2 = max
    a, b = map(int, input().split())
    print(partialMin(a + left_NodeStart - 1, b + left_NodeStart - 1))

4. 코드 후기
   아잇 뿌듯해~~!
   기존의 알고리즘에서 변형해야되는 부분이 핵심이었는데
   테케 따라가면서 고민하니까 아이디어가 짜졌다!!
   구간합과 다르게 두개씩 쌍을 이루면서 선택을 다르게 해야 됐었는데, 그로 인해 함수 코드도 달라지고
   중복이나 빠짐없이 다 선택돼서 다행이다,,,

코드 짜기가 어려울 땐 파트 씩 나눠 코드를 짜고 (partA, partB..) 그 파트가 제대로 수행됐는지 확인한 후 넘어가자! (partA -> partB)

ex. 최소 tree 형성 확인 후 -> 구간 최소 함수(partialMin) 코드 짜기