백준 1948

<임계경로>

난이도 : 플래티넘5

1. 백준 문제
   1948

2. 코드 알고리즘
   
   
   

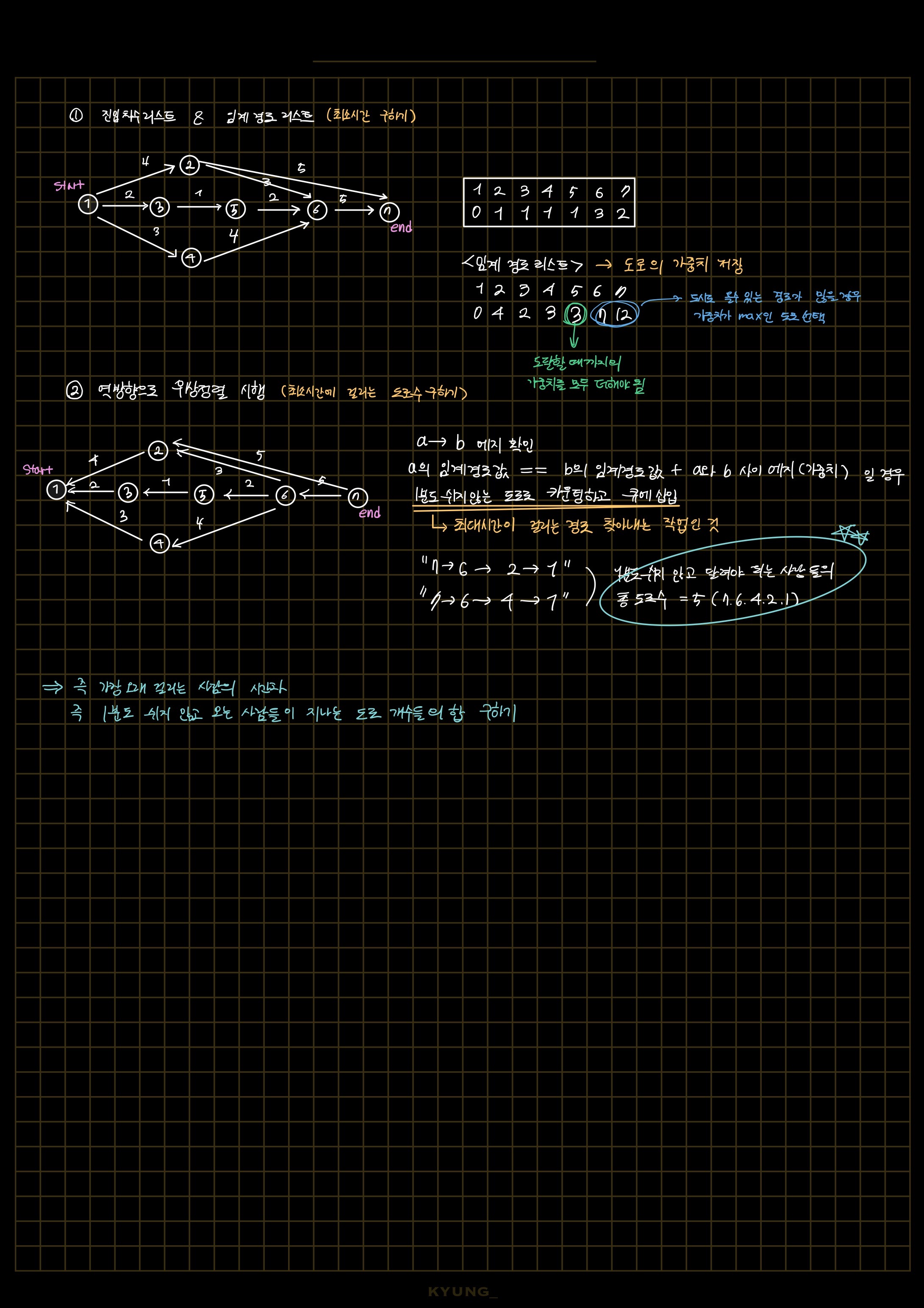
2-1. 슈도코드
(1번째 시도 슈도코드) //자료구조 바꿔야 됨

1948 슈도 코드

도시의 개수 N 입력받기
도로의 개수 M 입력받기
indegree 선언하기
A 인접리스트 선언하기
임계경로 weight 리스트 선언하기 (다 0으로 선언하기)

for m줄 동안 인접리스트 입력 받기
	a, b, c
	a에서 b 방향의 인접리스트 형성(A[a].append(b, c)) #c 가중치도 같이 저장하기 A[a] = [b,c]
	indegree[b] += 1

start와 end 노드 입력받기

#임계 경로 찾기
## 위상정렬 1 시행

queue1 선언하기

for 문 indegree 돌기 : (시작노드, 도착노드 상관없이 전체 도시에 대해 다 시행하기)
	indegree 값이 0인 노드 찾아서 queue에 넣기

while문:
	현재 노드 찾기
	for i in A[현재 노드]:
		weight[i] = max(weight[i], weight[현재 노드] + A[현재노드][-1]) #마지막 항
		if 문 indegree가 0 일경우 큐에 삽입

도착 노드 임계경로 값 출력하기

# 도로 개수 구하기

##역방향 인접리스트 구하기
B 역방향 인접리스트 선언
indegree2 리스트 선언

for 문 A 인접리스트:
	for j in A[i]:
		B[j].append(i)
		indegree2[i] += 1

## 위상정렬 2 시행

queue2 선언

for 문 indegree2 돌기: (indegree2 end 도시에서 시작하기, index가 -1 되도록, 출발 노드 까지만)
for i in range(end+1, start, -1)
	!end도시에서 시작하기 (end 도시에서 시작하도록)
	indegree 값이 0인 노드 찾아서 queue에 넣기

while문 :
	현재 노드 찾기
	for i in B[현재 노드]:
		if (현재 노드의 임계 경로 값 == i 의 임계 경로 값 + i와 현재 노드 사이 가중치) 일경우
			1분도 쉬지 않는 도로로 카운팅하고 큐에 삽입

카운팅한 도로 수 출력

3. 코드

• 1번째 시도 코드

# 1948
# https://www.acmicpc.net/problem/1948

import sys
input = sys.stdin.readline
from collections import deque

#도시의 개수 n 입력받기
n = int(input())
# 도로의 개수 m 입력받기
m = int(input())

#indegree 선언하기
indegree = [0]*(n+1)

#임계 경로 선언하기
weight = [0]*(n+1)

#인접리스트 선언하기
A = [[] for i in range(n+1)]

for i in range(1, m+1):
    a, b, c = map(int, input().split())
    A[a].append(b)
    A[a].append(c)
    indegree[b] += 1

start, end = map(int, input().split())

#임계 경로 찾기
## 위상 정렬 1 시행
queue1= deque()

for i in range(1, n+1):
    if indegree[i] == 0:
        queue1.append(i)

while queue1:
    now_node = queue1.popleft()
    for i in range(0, len(A[now_node]), 2):
        indegree[A[now_node][i]] -= 1
        weight[A[now_node][i]] = max(weight[A[now_node][i]], weight[now_node] + A[now_node][i+1])
        if indegree[A[now_node][i]] == 0:
            queue1.append(A[now_node][i])

print(weight[end]) #도착 노드 임계경로 값 출력하기
# 도로 개수 구하기

## 역방향 인접리스트 구하기
B = [[] for i in range(n+1)]
indegree2 = [0]*(n+1)

for i in range(1,n+1):
    for j in range(0, len(A[i]), 2):
        B[A[i][j]].append(i)
        B[A[i][j]].append(A[i][j+1])
        indegree2[i] += 1

## 위상 정렬 2 시행
queue2 = deque()
count = 0

for i in range(end, start-1, -1):
    if indegree2[i] == 0:
        queue2.append(i)

while queue2:
    now_node = queue2.popleft()
    for i in range(0, len(B[now_node]),2):
        if weight[now_node] == (weight[B[now_node][i]] + B[now_node][i+1]):
            count += 1
            queue2.append(B[now_node][i])

print(count)

-> 리스트에 튜플 형태로 저장하도록 수정
-> 위상정렬 2는 진입차수가 아닌 visited 리스트로 저장하도록 수정

• 2번째 시도 코드

# 1948
# https://www.acmicpc.net/problem/1948

import sys
input = sys.stdin.readline
from collections import deque

#도시의 개수 n 입력받기
n = int(input())
# 도로의 개수 m 입력받기
m = int(input())

#indegree 선언하기
indegree = [0]*(n+1)

#임계 경로 선언하기
weight = [0]*(n+1)

#인접리스트 선언하기
A = [[] for i in range(n+1)]
B = [[] for i in range(n+1)]

for i in range(1, m+1):
    a, b, c = map(int, input().split())
    A[a].append((b,c)) # ★튜플을 사용하자!!
    B[b].append((a,c))
    indegree[b] += 1

start, end = map(int, input().split())



#임계 경로 찾기
## 위상 정렬 1 시행
queue1= deque()

queue1.append(start) # ★출발도시만을 처음에 큐에 삽입

while queue1:
    now_node = queue1.popleft()
    for i in range(0, len(A[now_node])):
        indegree[A[now_node][i][0]] -= 1
        weight[A[now_node][i][0]] = max(weight[A[now_node][i][0]], weight[now_node] + A[now_node][i][1])
        if indegree[A[now_node][i][0]] == 0:
            queue1.append(A[now_node][i][0])
            
print(weight[end]) #도착 노드 임계경로 값 출력하기


# 도로 개수 구하기

## 역방향 인접리스트 구하기
visited = [0]*(n+1) #★indegree 리스트가 아닌 visited리스트 만들기


## 위상 정렬 2 시행
queue2 = deque()
count = 0

queue2.append(end)
visited[end]=1


while queue2:
    now_node = queue2.popleft()
    for i in range(0, len(B[now_node])):
        if weight[now_node] == (weight[B[now_node][i][0]] + B[now_node][i][1]):
            count += 1
            #만족하는 노드 중에서이전에 방문하지 않았을 경우 큐에 추가
            if visited[B[now_node][i][0]] == 0: #★방문하지 않았을 경우에만 큐에 추가(진입차수 관련X)
                visited[B[now_node][i][0]] = 1
                queue2.append(B[now_node][i][0])

print(count)

4. 코드 후기

1번째 코드 시간초과 -> 수정 -> 2번째 코드

• 튜플을 사용하자!
  자식 노드와 에지를 저장하는 데 튜플을 사용하지 않고 리스트에 차례대로 저장
  그래서 for문으로 2칸씩 뛰어 자식노드만을 추출했는데 이 과정에서 시간이 오래 소요됐을 가능성 존재

• 큐에 출발 / 도착 노드만을 삽입하자
  처음에 진입차수가 0인 모든 노드를 큐에 삽입할 필요 없다
  잉 왜?? 앞서 푼 위상정렬 문제와 다르게 왜 이번에는 출발/도착 노드만을 삽입하는 지 모르겠다.

• 역방향 인접리스트에서는 진입차수를 사용하지 않는다
  이것도 왜그러는지 모름ㅋ(다른 velog 봐야지)
  2번째 위상정렬에서는 진입차수로 다음 경로를 선택하는 것이 아닌 visited, 즉 방문 유무로 결정한다.

-> 튜플 사용에 익숙해지자!!

(그래도... 첫 시도도 되게 잘 풀었다 생각... 1번째 시도 시간초과만 났지 올바르게 실행은 됐음... 많이 수정하지도 않았고...
ㅎㅎ 뿌듯~~~ 나의 첫 플래티넘 문제!)