이 포스트는 책 '이것이 코딩 테스트다'를 토대로 작성하였습니다.

📌 서로소 집합 자료구조

서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조

'서로소 집합'이란?

공통 원소가 없는 두 집합

• 서로소 집합 자료구조는 union(합집합)과 find(찾기) 연산으로 구성된다.
  따라서 "union-find 자료구조"라고 불리기도 한다.
• 트리 자료구조를 이용하여 집합을 표현

👉 서로소 집합 계산 알고리즘

1. union 연산을 확인하여, 서로 연결된 두 노드 A, B를 확인한다.
   1-1. A와 B의 루트 노드 A', B'를 각각 찾는다.
   1-2. A'를 B'의 부모 노드로 설정한다. (B'가 A'를 가리키도록 한다.)
2. 모든 union 연산을 처리할 때까지 1번 과정을 반복한다.

🧐 예시

전체 집합 {1, 2, 3, 4, 5, 6}이 있고, 다음과 같은 4개의 union 연산이 주어져 있다고 하자.

    union 1,4     union 2,3     union2,4    union 5,6

union 연산을 순서대로 수행해보도록 하겠다.

union 연산들은 그래프 형태로 표현될 수 있다.
노드 : 전체 집합의 각 원소들
간선 : union 연산

step 0

• 초기 단계에는 전체 집합의 요소의 개수 크기의 부모 테이블을 초기화한다.
  그리고 이때 모든 노드들이 부모 노드로 자신을 가리키도록 초기화한다.
  

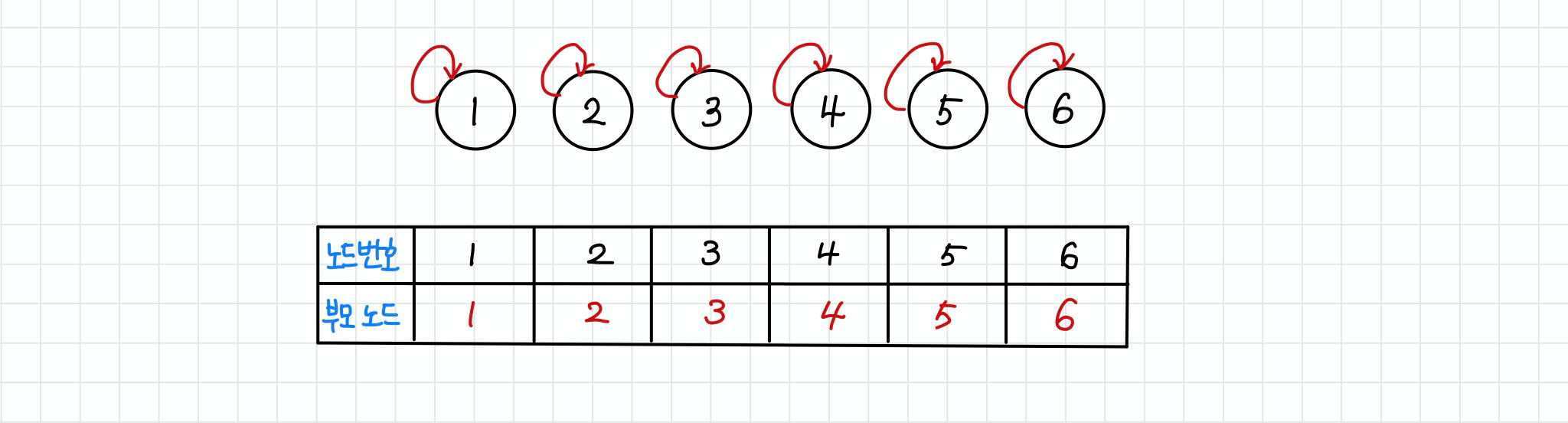
✔ step1 ~ step4 : union연산을 하는 대상 노드들의 루트 노드를 각각 찾아서, 더 큰 번호를 가진 루트 노드가 작은 번호를 가진 루트 노드를 가리키도록 부모 테이블을 갱신한다.

step 1 : union 1,4

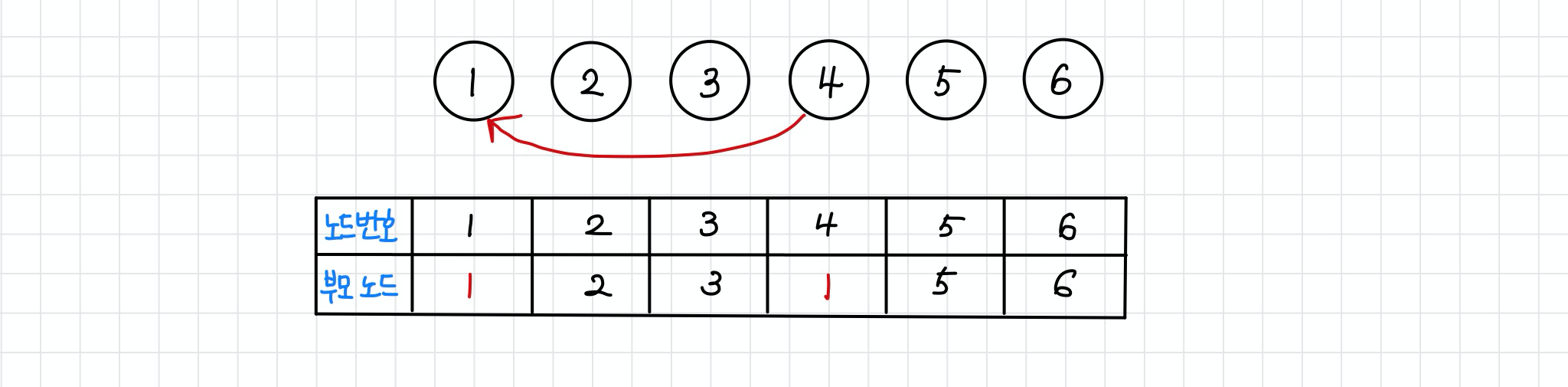
step 2 : union 2, 3

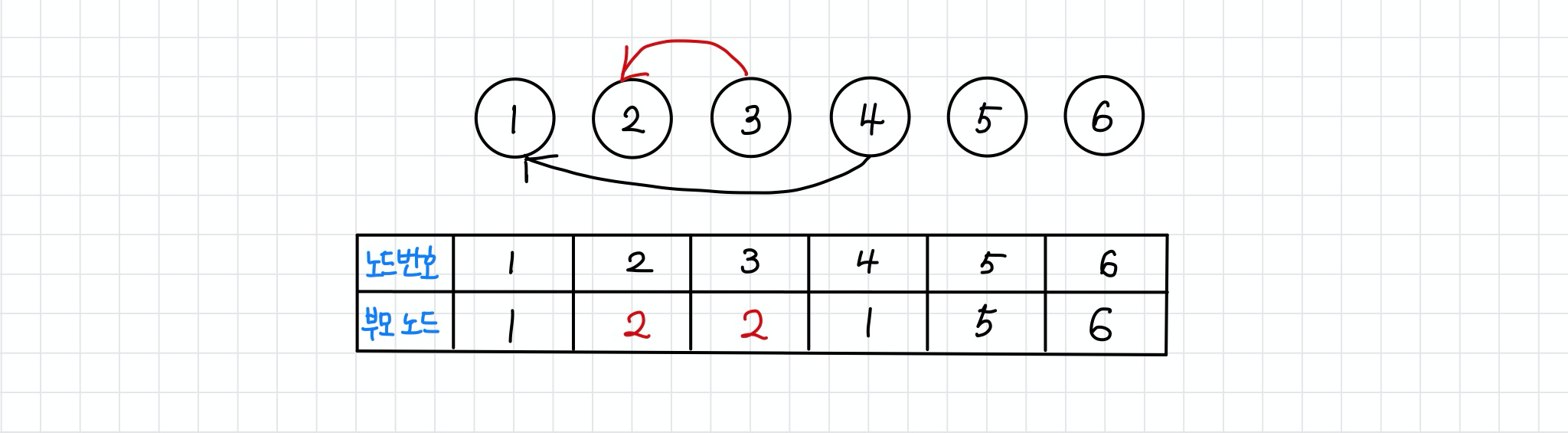
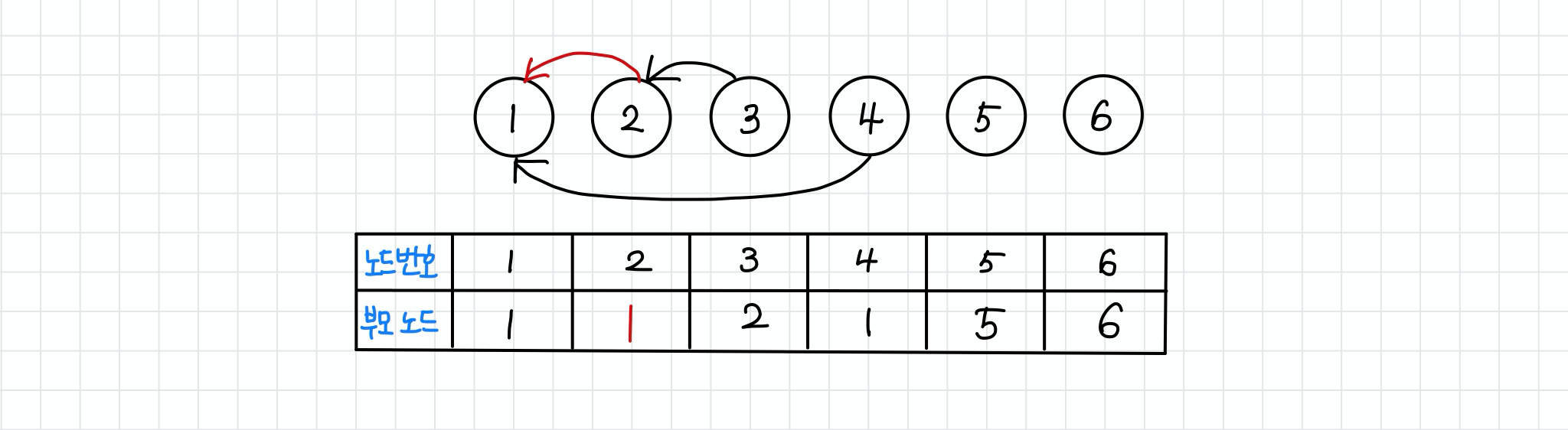
step 3 : union 2, 4

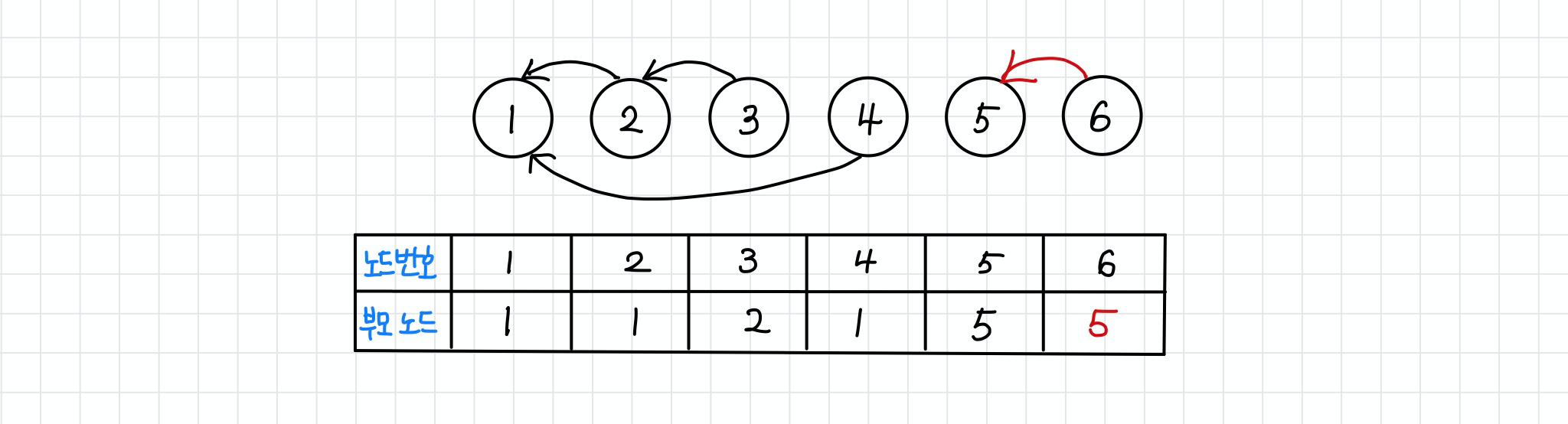
step 4 : union 5, 6

⌨ 기본적인 union, find 알고리즘 소스코드

1. find

• 특정 원소가 속한 집합을 찾는다.

def find_parent(parent,x):
    # 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if parent[x] != x:
        return find_parent(parent, parent[x])
    return x

2. union

• 두 원소가 속한 집합을 합친다.

def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

위의 기본적인 find 소스코드의 문제점

• 부모 테이블(parent)에 말 그대로 부모에 대한 정보만 담고 있기 때문에, 실제로 루트를 확인하고자 할 때 재귀적으로 부모를 거슬러 올라가게 된다.
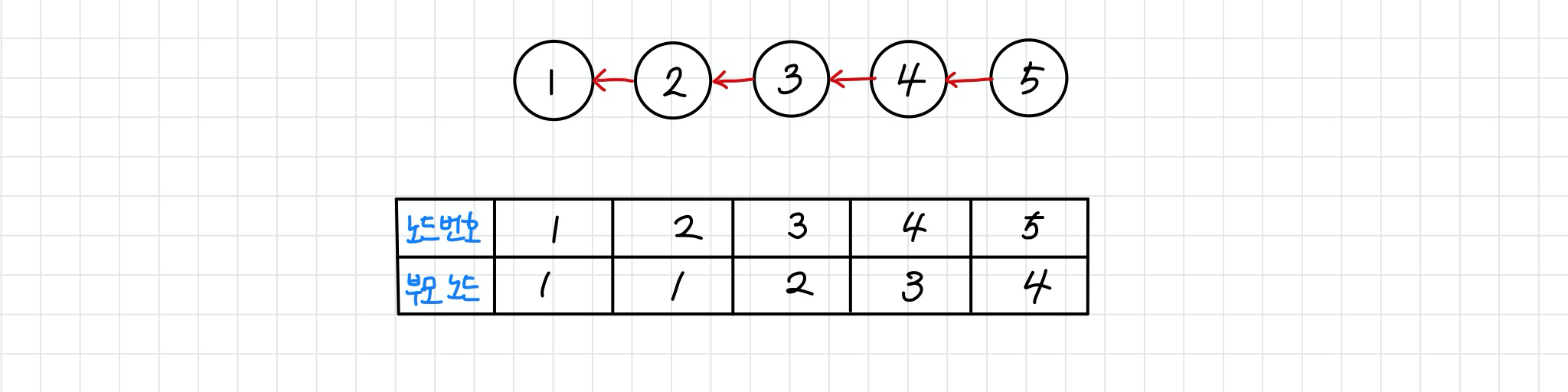
  -> 따라서 find함수가 비효율적으로 동작한다.
• 예시) 전체 집합 {1, 2, 3, 4, 5}이 있고, 4개의 union 연산이 순서대로 (4, 5), (3, 4), (2, 3), (1, 2)로 주어졌다고 하자.
  
  위 그림에서 모든 원소들의 루트 노드 값은 1이지만, 부모 노드 값은 순서대로 1,1,2,3,4임을 알 수 있다.
  이때 예를들어, 노드 5의 루트 노드를 찾기 위해서는 최대 O(V)의 시간이 소요된다. (노드5 -> 노드4 -> 노드3 -> 노드2 -> 노드1로 거슬러 올라감)
  결국 위의 find 알고리즘을 쓴다면 노드의 개수가 V개이고 find/union 연산의 개수가 M개일 때, 전체 시간 복잡도는 O(VM)이 되어 비효율적이다.

---

⌨ 경로 압축 find 알고리즘 / 코드

• 경로 압축(Path Compression)은 find 함수를 재귀적으로 호출한 뒤에 부모 테이블값을 바로 갱신하는 기법이다.
• 경로 압축 방식을 사용하면 find함수를 호출한 이후에는 부모 노드가 바로 루트 노드가 된다. 따라서 루트 노드에 좀 더 빠르게 접근할 수 있다.

def find_parent(parent, x):
    if parent[x] != x:
        parent[x] = find_parent(parent, parent[x])
    return parent[x]