이 글을 시작으로, 데이터분석의 꽃이라고 할 수 있는(?) 전처리에 관해 이야기를 나눠보겠습니다. 먼저, 오늘은 feature selection에 관해 이야기합니다.
Feature selection
ML에서 모델 입력 변수 중 가장 중요한 변수를 선택해서 모델의 성능을 최적화하는 것이다. 무조건적인 feature selection은 모델 성능에 좋지 않습니다. 오히려 당연한 결과, 누구나 아는 결과를 만들거나 왜곡된 결과를 만들 수 있다.
피처가 많으면, 차원의 저주, 해석의 어려움, 과적합 ... 등등의 이유가 발생할 수 있으므로, 도메인을 통해 피처를 잘 선택해야 한다.
먼저, 필터 방식에 관해 이야기를 나눠보겠습니다.
Filter Method (필터방식)
데이터의 통계적인 특성에 기반하여 중요도를 평가하고 선택하는 방식
- 상관계수 (Correlation Coefficient) : 특성과 타겟 변수간의 상관관계 제거
- 분산 (Variance Threshold) : 분산이 너무 작은 특성을 제거하는 방식
- 카이제곱 테스트 (Chi-Square Test) : 범주형 데이터 타겟과 독립성 테스트를 통해서 제거 or 선택
-> 제거에 대한 기준 임계점이 필요하며, 임계점은 도메인과 함께 다른 피쳐들과 비교해야한다.
상관계수
1. 독립변수와 종속변수와의 관계
종속변수와 상관관계가 높은 변수는 선택!
#data 생성
np.random.seed(111)
n_samples=1000#특성 피처 생성
X1 = np.random.rand(n_samples) * 100 # X1 y와 상관관계가 높도록 설정
X2 = np.random.rand(n_samples) * 100 # X2도 y와 상관관계 높다.
X3 = np.random.rand(n_samples) * 100
X4 = np.random.rand(n_samples) * 100
# X1, X2 강하게 의존하는 형태, 나머지는 거의 영향이 없음
y = 3*X1 + 2*X2 + np.random.randn(n_samples)*10
#상관계수 확인하기
df.corr()
#y에 대한 상관계수 matrix
corr_matrix = df.corr()['y'].drop('y')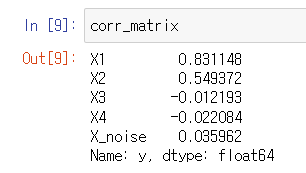
#0.5 특성만 뽑기
threshold = 0.5
selected_features = corr_matrix[abs(corr_matrix)>threshold].index
print(selected_features)selected feature만 사용했을 때와 전체 특성을 사용했을 때와 비교
#Linear Regression
X_selected = df[selected_features]
X_train, X_test, y_train, y_test = train_test_split(X_selected, df['y'], test_size=0.2,random_state=111)
#모델학습
model = LinearRegression()
model.fit(X_train, y_train)
#예측 MSE
y_pred =model.predict(X_test)
mse_selected = mean_squared_error(y_test, y_pred)
print('mse_selected', mse_selected)- selected feature의 성능이 더 좋다.
- 선형적인 회귀분석이므로 더 좋은 결과가 나올 것으로 예측해볼 수 있다.
- (주의) 도메인 없이 상관분석의 결과만으로 피처의 사용 여부를 결정하는 것은 위험하다. 지금은 이해를 돕기 위한 예시일 뿐이다.
2. 독립변수와 독립변수와의 관계 (피처들 간의 관계)
피처간의 상관관계가 높으면 제거!
: 상관관계가 높은 변수끼리는 유사한 양상으로 움직인다는 것, 같이 움직이므로 선형회귀에서 오차 계산 등이 오차 값이 계산될 대 더 큰 영향을 준다.
: 다중공선성의 문제, 다중공선성이 높은 피처들은 제거
## 특성 피처들 생성
X1 = np.random.rand(n_samples) * 100
X2 = X1+np.random.rand(n_samples) * 10 # X1과 매우 높은 상관관계
X3 = np.random.rand(n_samples) * 100
X4 = np.random.rand(n_samples) * 100
X_noise = np.random.rand(n_samples) * 100
# y는 X1, X3 강하게 의존하는 관계
y = 3*X1 + 2*X3 + np.random.randn(n_samples) * 10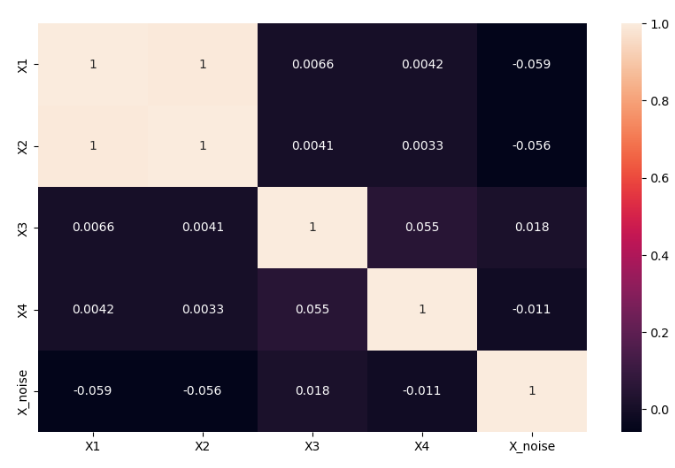
X1과 X2는 상관계수가 굉장히 높은 것을 확인할 수 있다.
# 상관계수가 threshold 0.8 이상인 경우는 제거를 한다.
threshold = 0.8
to_drop = set()
#상관계수가 높은 피처만 출력
for i in range(len(corr_matrix.columns)):
for j in range(i):
if abs(corr_matrix.iloc[i,j]) > threshold:
to_drop.add(corr_matrix.columns[i])
print(to_drop)
#원하는 피처만 제거함
X_reduced =df.drop(columns=list(to_drop)+['y'])
X_train, X_test, y_train, y_test = train_test_split(X_reduced, df['y'], test_size=0.3, random_state=111)selected feature만 사용했을 때와 전체 특성을 사용했을 때와 비교
# 상관계수가 높은 피처를 제거했을 때
#모델학습
model = LinearRegression()
model.fit(X_train, y_train)
#예측 MSE
y_pred =model.predict(X_test)
mse_selected = mean_squared_error(y_test, y_pred)
print('mse_selected', mse_selected)- 전체 특성이 들어갔을 때의 성능이 더 좋다. 즉, 무조건적으로 feature selection을 하는 것은 옳지 않다.
분산
분산이 작은 피처는 거의 변화가 없기 때문에, 학습 기여를 덜 한다는 가정 하에 임계값을 정해서 피처를 제거한다.
1. VarianceThreshold
-
threshold: 분산이 이 값 이하인 피처를 제거합니다. 기본값은0.0으로, 분산이 0인 피처만 제거합니다. -
fit(X): 각 피처의 분산을 계산하여, 임계값에 따라 피처 선택 준비.
-
fit_transform(X): fit을 수행한 후, 선택된 피처들만 변환하여 반환.
-
transform(X): 학습된 기준을 바탕으로 피처 선택을 적용.
-
get_support(indices=False): 선택된 피처의 인덱스나 Boolean 마스크 반환.
-
inverse_transform(X): 선택되지 않은 피처들을 0으로 채워서 원래 공간으로 복원.
2. SelectKBest
-
score_func: 각 피처의 중요도를 평가하기 위한 통계적 검정 함수입니다. 주요 함수는 아래와 같습니다:chi2: 카이제곱 검정을 사용한 피처 선택.f_classif: ANOVA F-값을 사용한 피처 선택 (연속형 변수와 범주형 변수 간의 관계 분석에 유용).mutual_info_classif: 상호 정보량을 기반으로 피처 선택.
-
k: 선택할 피처의 수. 기본값은 10개이며, k개의 상위 피처를 선택합니다.
- fit(X, y): 주어진 X와 y 데이터에 대해 카이제곱 값을 계산하여 상위 k개의 중요한 피처를 찾습니다.
- fit_transform(X, y): fit과 동시에 선택된 피처들로 변환된 데이터셋을 반환합니다.
- transform(X): 학습된 기준에 따라 상위 k개의 피처만 선택하여 반환합니다.
- get_support(indices=True): 선택된 피처의 인덱스를 반환하거나, Boolean 마스크를 반환하여 어떤 피처가 선택되었는지 확인합니다.
- scores_: 각 피처의 카이제곱 점수를 확인할 수 있습니다.
- pvalues_: 각 피처의 p-value 값을 확인하여, 해당 피처가 종속변수에 유의미한 영향을 미치는지를 평가합니다.
# 분산에 대한 예시 코드
from sklearn.feature_selection import VarianceThreshold
X = [[0,2,0,3],
[0,1,2,3],
[0,1,1,5]]
#threshold = 0.2
selector = VarianceThreshold(threshold=0.2)
X_high_variance = selector.fit_transform(X)
X_high_variance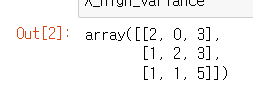
첫 번째 feature가 제거된 것을 확인할 수 있다.
보통 임계값은 0.1~0.5로 잡지만, 이것 역시 도메인에 따라 달라진다. 여러 실험에 걸쳐 결정할 수 있다.
카이제곱 (Chi2)
관측된 데이터와 기대되는 데이터의 차이를 계산
이 값이 높다는 것은 해당 피처가 종속변수와 강한 연관성이 있다는 것이다. 즉, 중요한 피처라고 판단할 수 있다.
from sklearn.feature_selection import SelectKBest, chi2
import numpy as np
X = np.array([[1,2,3],
[4,5,6],
[7,8,9],
[10,11,12]])
y = np.array([0,1,0,1])#상위 2개 피처 선택
selector = SelectKBest(chi2, k=2)
X_new = selector.fit_transform(X, y)
X_new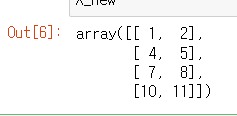
첫 번째, 두 번째 피처들이 선택된 것을 확인할 수 있다.
그럼 이제 가장 많이 사용하는 데이터셋인 타이타닉 데이터를 활용하여 feature selection을 해보겠습니다.
타이타닉 데이터로 해보는 feature selection
먼저, 데이터를 불러온다.
tt = sns.load_dataset('titanic')
tt.head()결측치를 확인하고 처리한다.
#결측치 확인
tt.info()#결측치 처리
tt['age'].fillna(tt['age'].median(), inplace=True)
tt['embark_town'].fillna(tt['embark_town'].mode()[0], inplace=True)사용할 피처를 정의한다.
#사용할 피처
X = tt[['pclass', 'sex', 'age', 'fare', 'embark_town']]
y = tt['survived']#연속형 변수인 age, fare를 분위수로
X.loc[:, 'age_binned'] = pd.qcut(X['age'], q=4, labels=False)
X.loc[:, 'fare_binned'] = pd.qcut(X['fare'], q=4, labels=False)
X = X.drop(['age','fare'], axis=1)#OneHotEncoder
onehot_encoder = OneHotEncoder(sparse_output=False, drop='first')
X_encoded = onehot_encoder.fit_transform(X)feature selection
chi_selector = SelectKBest(chi2, k='all')
X_selected_all = chi_selector.fit_transform(X_encoded, y)
chi_scores = pd.DataFrame({'Feature': onehot_encoder.get_feature_names_out(X.columns),
'Score': chi_selector.scores_}).sort_values(by='Score', ascending=False)
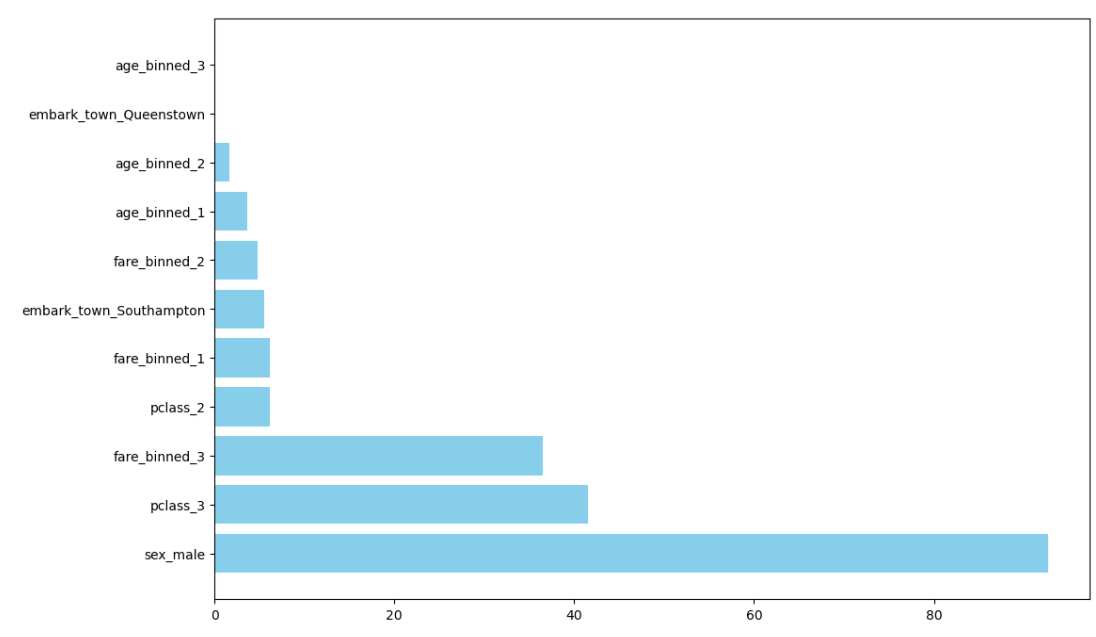
chi_scores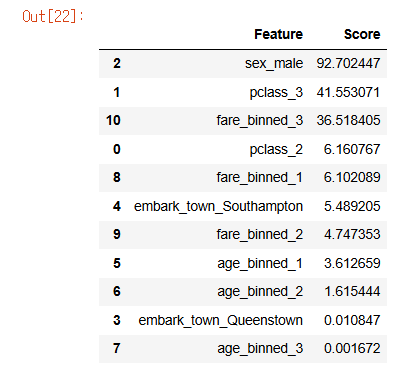
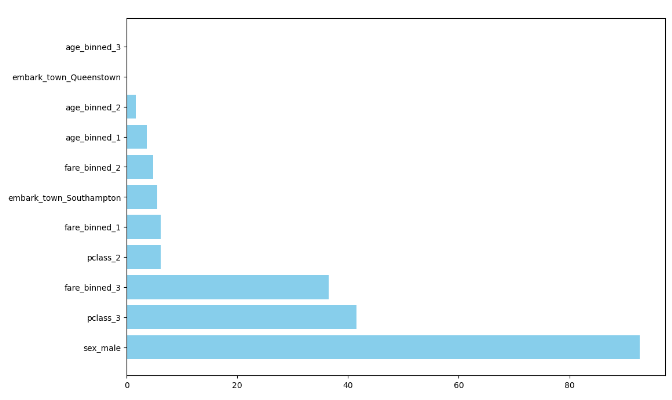
sex와 pclass, fare가 생존율에 큰 영향력을 주고 있는 중요한 피처임을 확인할 수 있습니다.
추가로, 은행에서 특정 마케팅 캠페인의 성공 여부를 예측하는 데 쓰이는 데이터셋을 가지고 feature selection을 진행해보았습니다.
은행 캠페인 데이터로 해보는 feature selection
feature 확인
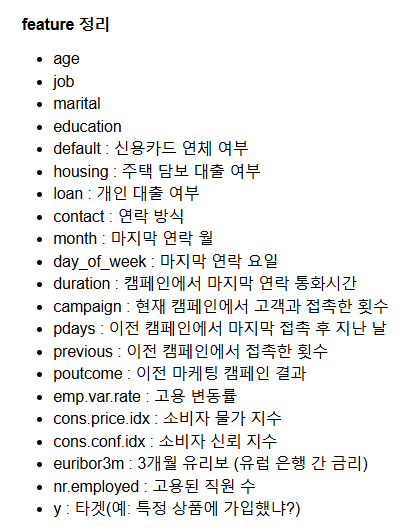
도메인 지식이 부족할 땐, feature에 관해 해석을 정리해두는 것이 도움이 된다.
상관관계
상관계수가 0.9이상인 피처들은 삭제하여 차원을 줄여주었다.
correlation_matrix = X.corr().abs()
upper_triangle = correlation_matrix.where(np.triu(np.ones(correlation_matrix.shape), k=1).astype(bool))
# 상관관계가 threshold 이상인 컬럼 제거
to_drop = [column for column in upper_triangle.columns if any(upper_triangle[column] > 0.9)]
X_reduced = X.drop(columns=to_drop)
X_reduced범주형 변수: 카이제곱 검정
from sklearn.feature_selection import SelectKBest, chi2
# 범주형 변수에 대한 카이제곱 검정 적용
X_categorical = X_reduced.select_dtypes(include=['object'])
X_encoded = pd.get_dummies(X_categorical, drop_first=True) # 일시적 one-hot encoding
selector = SelectKBest(chi2, k=15) # 상위 10개 피처 선택
X_selected = selector.fit_transform(X_encoded, y)
chi_scores = pd.DataFrame({'Feature': X_encoded.columns[selector.get_support()],
'Score': selector.scores_[selector.get_support()]}).sort_values(by='Score', ascending=False)
chi_scores연속형 변수: 분산
from sklearn.feature_selection import VarianceThreshold
X_numerical = X_reduced.select_dtypes(include=['number'])
selector = VarianceThreshold(threshold=0.4)
X_high_var = selector.fit_transform(X_numerical)
selected_feature = X_numerical.columns[selector.get_support()]
selected_featurevariances = X_numerical.var(axis=0)
feature_names = X_numerical.columns
# 각 피처의 이름과 분산을 출력
variance_info = pd.DataFrame({'Variance': variances}).sort_values(by='Variance', ascending=False)
variance_info추가) Sequential Feature Selection (SFS)
from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.linear_model import LogisticRegression
# 로지스틱 회귀 모델을 사용하여 순차적 특성 선택
model = LogisticRegression()
sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='forward')
X_selected = sfs.fit_transform(X_encoded, y)
X_selected변수의 데이터 타입에 따라 나눠서 진행해보았다. 한 번에 보기 위해 OneHotEncoder를 활용해볼 수는 있으나, 차원이 커지는 문제가 있어서 이를 피하기 위해 따로 보았다.
데이터 유출을 막기 위해 정확한 결과는 게시할 수 없으나, 생각보다 유의미한 결과가 나와서 신기했다.
이렇게 feature selection에 관해 알아보고, 간단한 코드 실습으로 이해해보았습니다. 사실, 학교 수업 등에서 이미 알고 있었던 개념들이었지만, 어떻게 feature selection에 적용되는지는 잘 모르고 있었습니다. 실습을 통해 그동안 배웠던 개념들이 어떻게 쓰이는지 적용해볼 수 있어서 좋았습니다 !