목차
1. Spanning Tree(신장 트리)란?
spanning tree(신장 트리)는 모든 정점이 간선으로 연결되어 있고 간선의 개수가 정점 개수보다 하나 적은 그래프를 의미합니다.
신장 트리의 조건
1. 모든 정점이 간선으로 연결 되어 있어야 한다.
2. 간선의 개수는 정점 개수 - 1 이어야 한다.
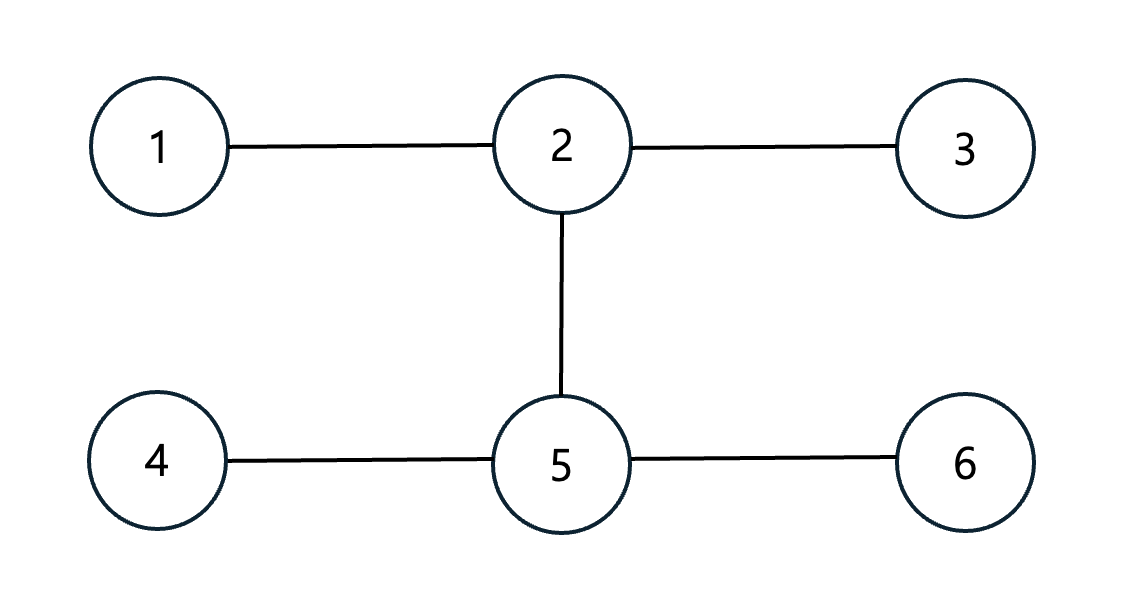
Spanning Tree 예시
2. Minimum Spanning Tree(최소 신장 트리)란?
Minimum Spanning Tree(최소 신장 트리)는 그래프에서 만들 수 있는 신장 트리 중 간선의 가중치의 합이 최소가 되는 트리를 의미합니다. 최소 신장 트리는 주로 MST로 부릅니다.
MST의 조건
1. 신장 트리의 조건을 만족해야 한다.
2. 간선 가중치의 합이 최소가 되어야 한다.
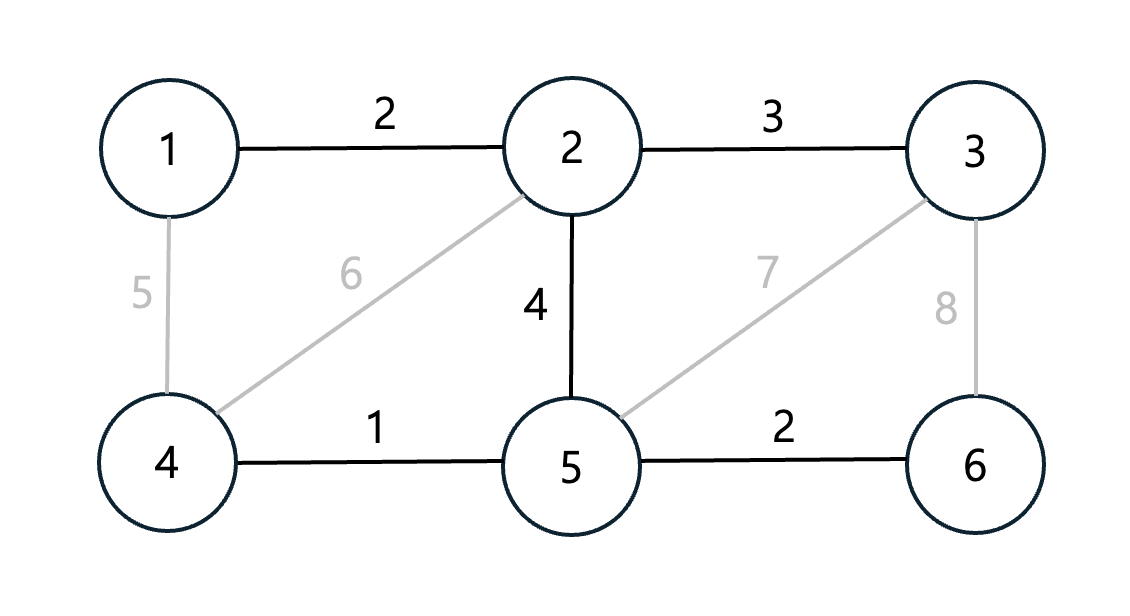
MST 예시
3. MST의 사용 예시
MST는 도시 간 도로망 최적화, 통신 네트워크 설계, 전력망 최적화, 물류 네트워크 설계 등 다양한 분야에서 사용 됩니다.
4. MST를 구하는 방법
이제 간선의 가중치가 주어진 그래프에서 MST를 구하는 방법에 대해 소개하겠습니다. MST를 구하는 알고리즘은 프림 알고리즘과 크루스칼 알고리즘이 있습니다.
4.1 프림 알고리즘
프림 알고리즘(Prim's Algorithm)의 단계는 다음과 같습니다.
프림 알고리즘에서 MST를 구하는 과정
1. 임의의 정점 하나를 선택해서 MST에 추가합니다.
2. 최소 신장 트리와 연결되어 있는 정점 중 가장 가중치가 적은 정점을 MST에 추가합니다. 단, 순환을 형성하지 않는 정점을 추가해야 합니다.
3.과정 2를 신장 트리 조건에 만족할 때 까지 반복합니다.
프림 알고리즘의 과정을 시각화 해보겠습니다.
프림 과정 시각화
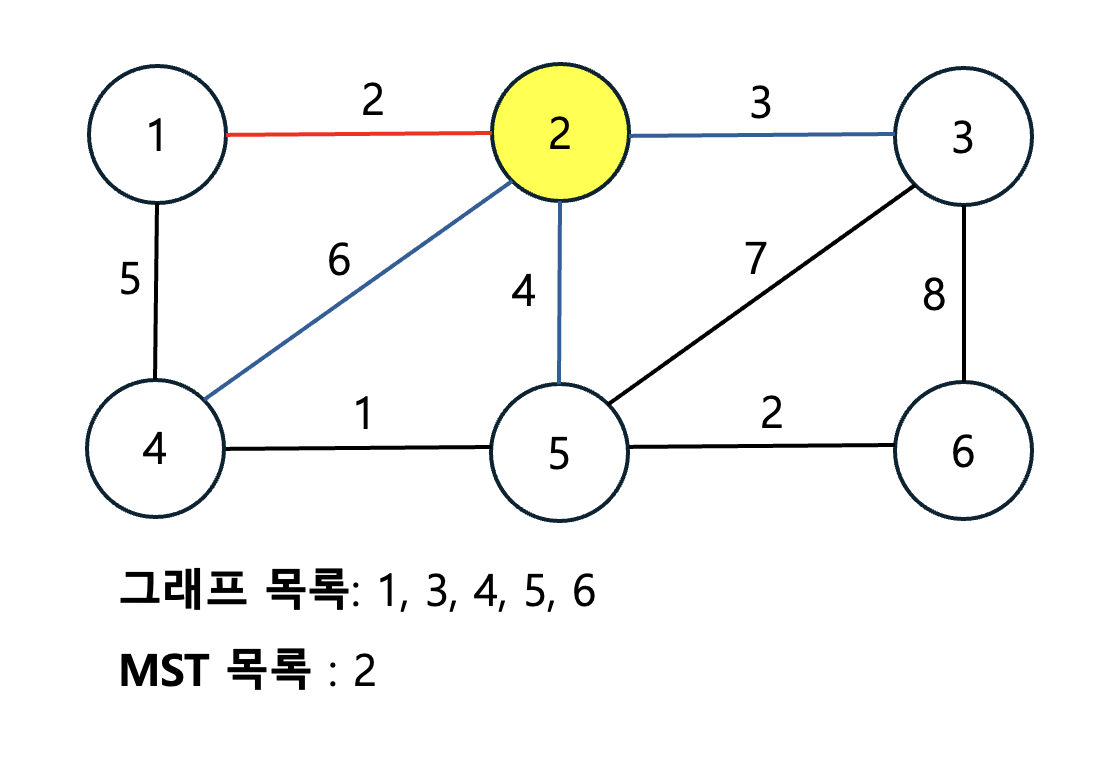
정점 2번을 임의로 선택한 후, MST 목록에 추가했습니다. 그 다음 MST에 있는 간선들 중 가장 작은 가중치가 있는 간선으로 이동합니다. 파란색과 빨간색 간선은 MST에 연결된 간선입니다. 그 중 빨간선은 MST의 간선으로 연결된 간선입니다. 즉, 가중치가 최소인 간선입니다.
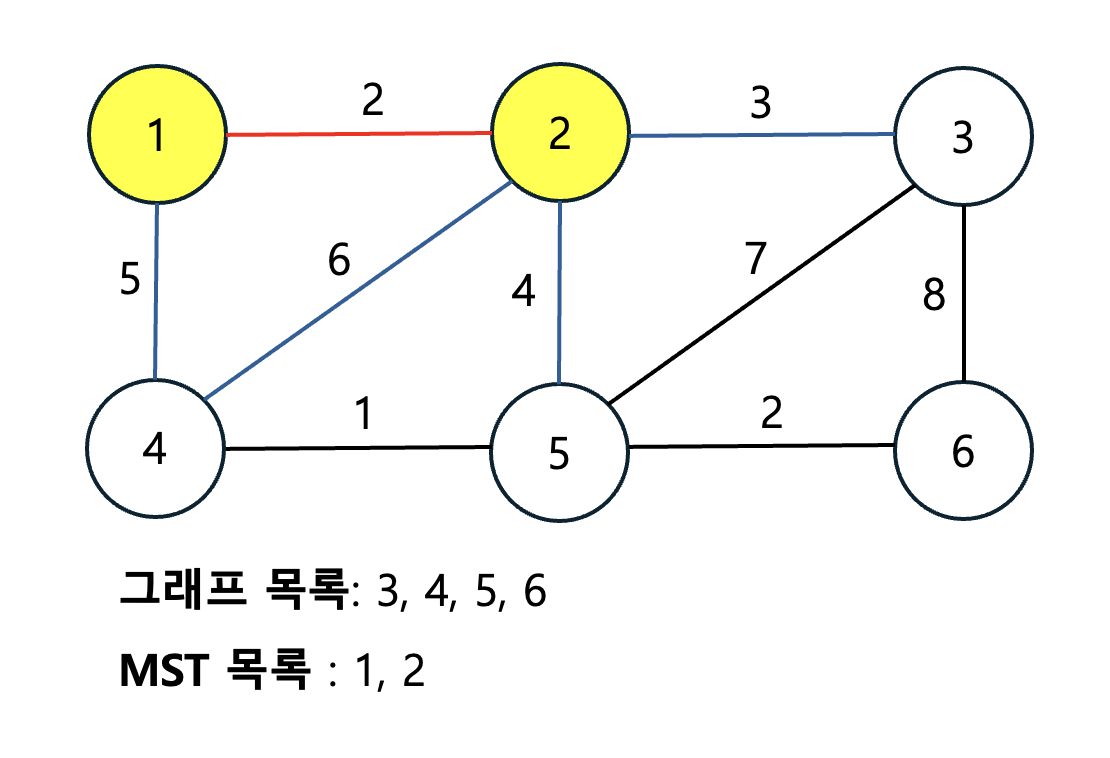
MST가 1, 2번 정점으로 확장되었습니다. MST의 간선의 가중치는 2, 3, 4, 5, 6이 있습니다. 그 중 2번은 이미 연결되어 있기 때문에, 그 다음 최소 가중치인 3인 간선이 연결됩니다.
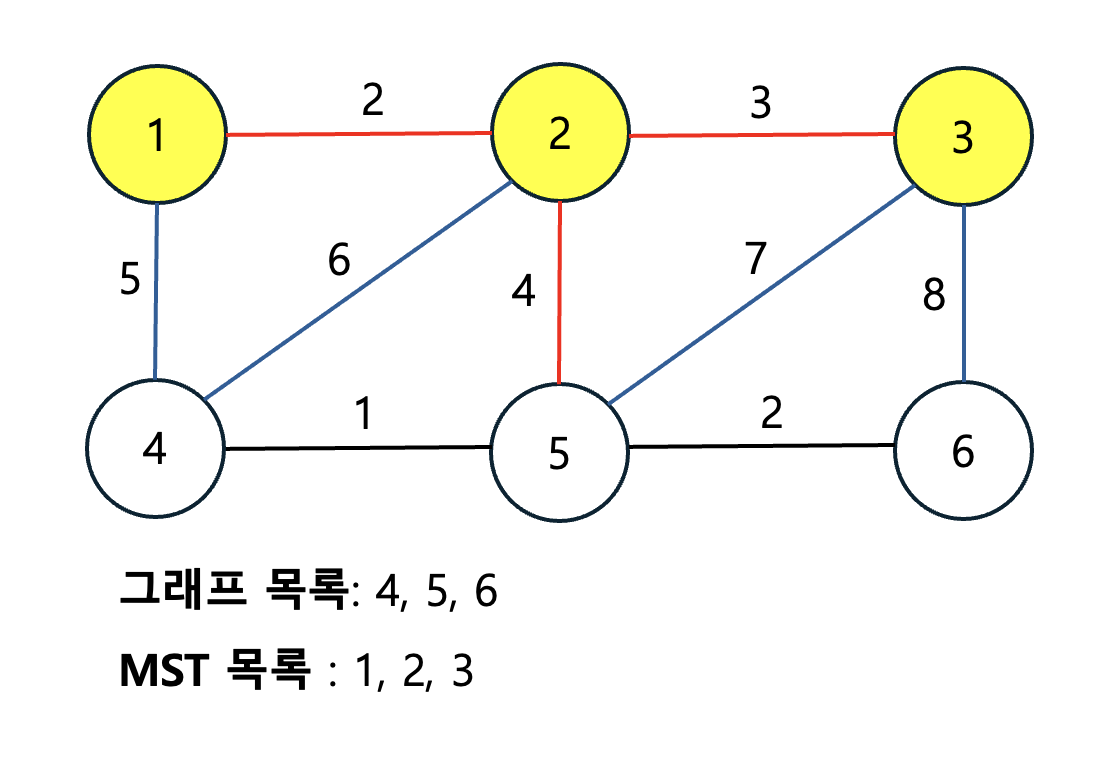
MST의 정점이 1, 2, 3으로 늘어났으므로 이에 따른 간선도 추가해줍니다. 그리고 가중치가 가장 낮으면서 사이클을 만들지 않는 간선을 선택합니다. 이제 그림만 나열하겠습니다.
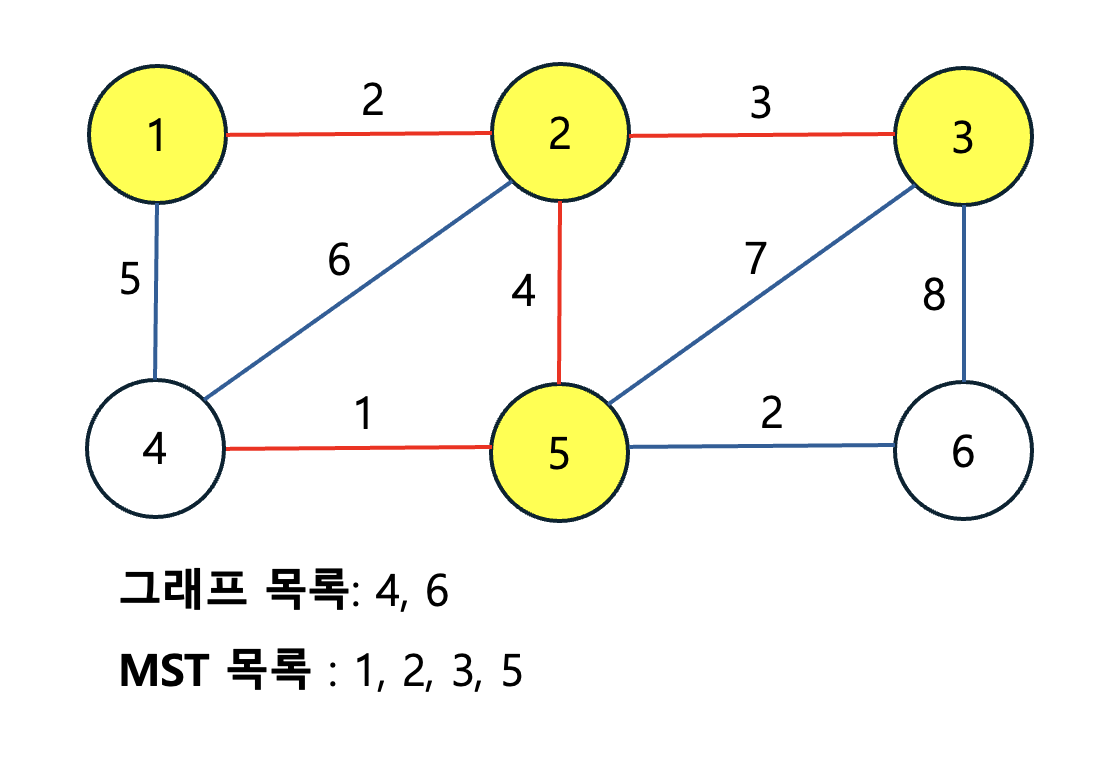
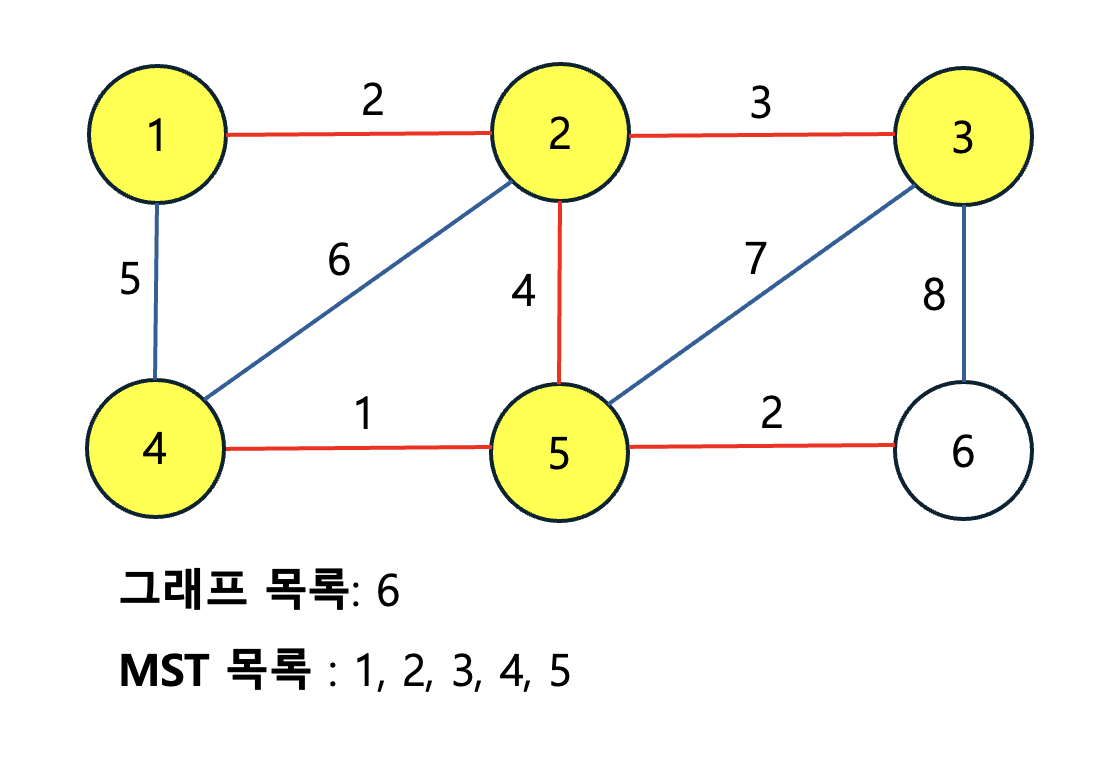
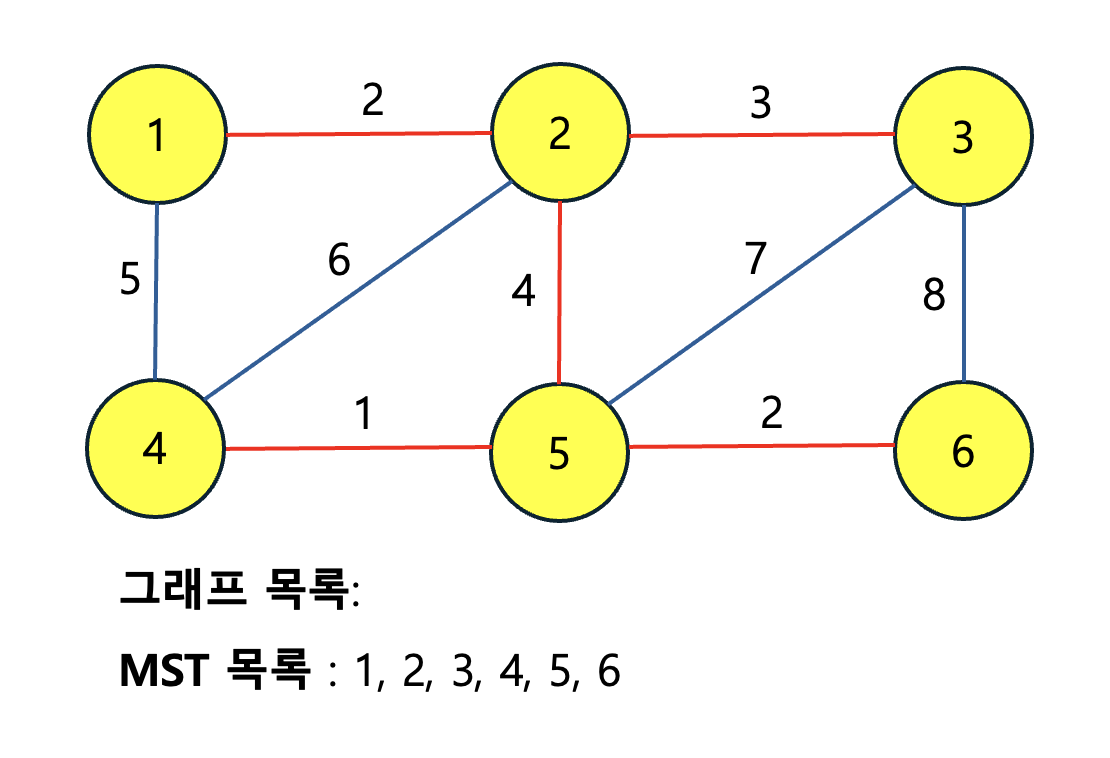
이렇게 MST가 완성되었습니다. 부분 MST의 간선을 확장할 땐 반드시 이미 포함된 간선은 아닌지 확인한 후 확장해야 합니다.