[Algorithm] DFS(Depth First Search)

💡 동작원리

이 글에서는 DFS(깊이우선탐색)에 대해 다뤄보려고 한다. DFS는 그래프 탐색의 방법 중 하나이다. 그래프를 탐색할 때, vertice(정점)에 있는 edge(간선) 중 하나를 선택해 이동하고, 다음 vertice에서 또 한 edge를 선택해 이동하고, 이를 반복하다가 더 이상 이동할 수 없게 되면 이전의 vertice로 돌아와서 다른 edge를 선택해 이동하며 그래프를 탐색하는 방법을 DFS라고 한다.

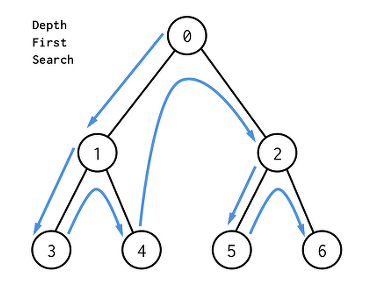
DFS를 구현할 때는 stack(스택) 자료구조를 이용한다. 왜냐하면 가장 마지막에 들어간 데이터가 가장 먼저 나오는 stack의 원리를 이용하여 바로 이전의 vertice를 쉽게 찾을 수 있기 때문이다. 제일 처음 방문하는 vertice에 있는 edge 중 하나를 택해 다음 vertice로 이동하고, 방문한 vertice를 stack에 넣는다. 이를 반복하여 가장 깊은 곳의 vertice까지 방문하고, edge가 없게 되면 이때 stack의 top에 있는 바로 이전의 vertice를 꺼내, 아까 탐색하지 않았던 edge로 이동한다. 이 반복하여 그래프의 모든 vertice를 탐색하는 방법이 DFS이다.

💻 코드

void DFS(int Vertice){
	Visited[Vertice] = true;
	cout << Vertice << " ";
	for (int i = 0; i < Graph[Vertice].size(); i++){
		int Edge = Graph[Vertice][i];
		if (!Visited[Edge])
			DFS(Edge);
	}
}

위 코드는 DFS의 간단한 코드이다. 💡 동작원리에서 설명한 것과는 달리 stack 자료구조를 사용하지 않고 구현되어 있다. 그 이유는 DFS를 재귀함수 형식으로 짜게 되면, 자연스럽게 재귀함수를 호출하게 되면 stack 자료구조를 만들어내기 때문이다. 이제 DFS 코드에 대해 설명하겠다. 먼저 Vertice를 입력받으면 탐색했다고 저장하고 출력한다. 이후 이 Vertice에 붙어 있는 Edge들을 통해 다음 Vertice로 이동한다. 이때 제일 처음 나오는 Edge를 통해 다음 Vertice로 넘어기 위해 DFS 함수를 재귀로 호출해준다. 이렇게 DFS 방식으로 그래프를 탐색한다.

⏱ 시간복잡도

DFS의 시간복잡도는 $O(|V|+|E|)$이다. $|V|$는 Vertice의 개수, $|E|$는 Edge의 개수이다.

$O(|V|+|E|)$