[Algorithm] Insertion Sort

💡 동작원리

이 글에서는 Insertion Sort(삽입정렬)에 대해 다뤄보려고 한다. Insertion Sort(삽입정렬)의 원리는 인덱스가 1부터 N-1까지의 원소를 순서대로 하나씩 제 위치를 찾아서 삽입하며 정렬하는 것이다.

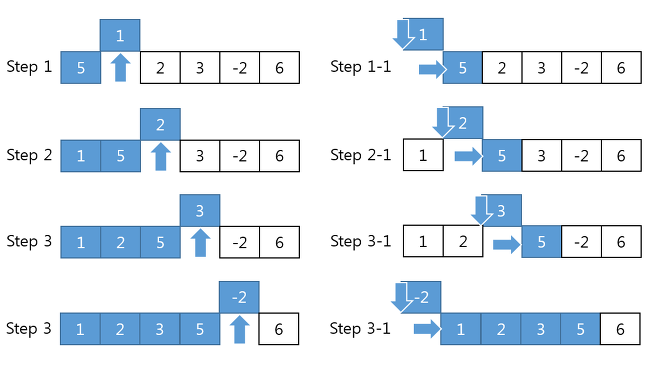
위 그림은 오름차순으로 정렬하는 Insertion Sort(삽입정렬)의 동작원리를 그림으로 표현한 것이다. 1번 원소부터 N-1번 원소의 위치를 찾아서 그 사이에 넣고 배열을 뒤로 미는 것을 확인할 수 있다. i번째 원소의 위치를 찾는 과정은 다음과 같다. i-1, i-2, ... 를 하나씩 탐색해, i번째 원소보다 더 크면 뒤로 한칸씩 밀고, i번째 원소보다 작은 원소가 나타나면 탐색을 멈추고 그 자리에 i번째 원소를 삽입한다. 이것이 Insertion Sort(삽입정렬)이다.

💻 코드

void Insertion_Sort(){
    for (int i = 1; i < N; i++) {
    	int temp = Arr[i];
        int j;
        for(j = i - 1; j >= 0; j--){
            if(Arr[j] > temp) Arr[j + 1] = Arr[j];
            else break;
        }
        Arr[j + 1] = temp; 
    }
}

⏱ 시간복잡도

Insertion Sort(삽입정렬)는 i번째 원소의 위치를 찾는 과정에서의 연산 횟수가 일정하지 않아서 최선의 경우와 최악의 경우로 나뉘게 된다.

먼저 최선의 경우를 살펴보자. 최선의 경우는 모두 한 번만에 i번째 원소의 위치를 찾게 되는 것이기 때문에 연산 횟수가 N-1이 된다. 따라서 시간복잡도는 $O(N)$이다.

최악의 경우를 살펴보자. 최악의 경우에는 모든 i번째 원소에 대하여 위치를 찾을 때, i-1번째 원소부터 0번째 원소를 탐색하는 것이다. 따라서 연산 횟수가 $1 + 2 + ... + N-1 = N(N-1)/2$이므로 시간복잡도는 $O(N^2)$이다.

Best case : $O(N)$
Worst case : $O(N^2)$