골드바흐의 추측이란?
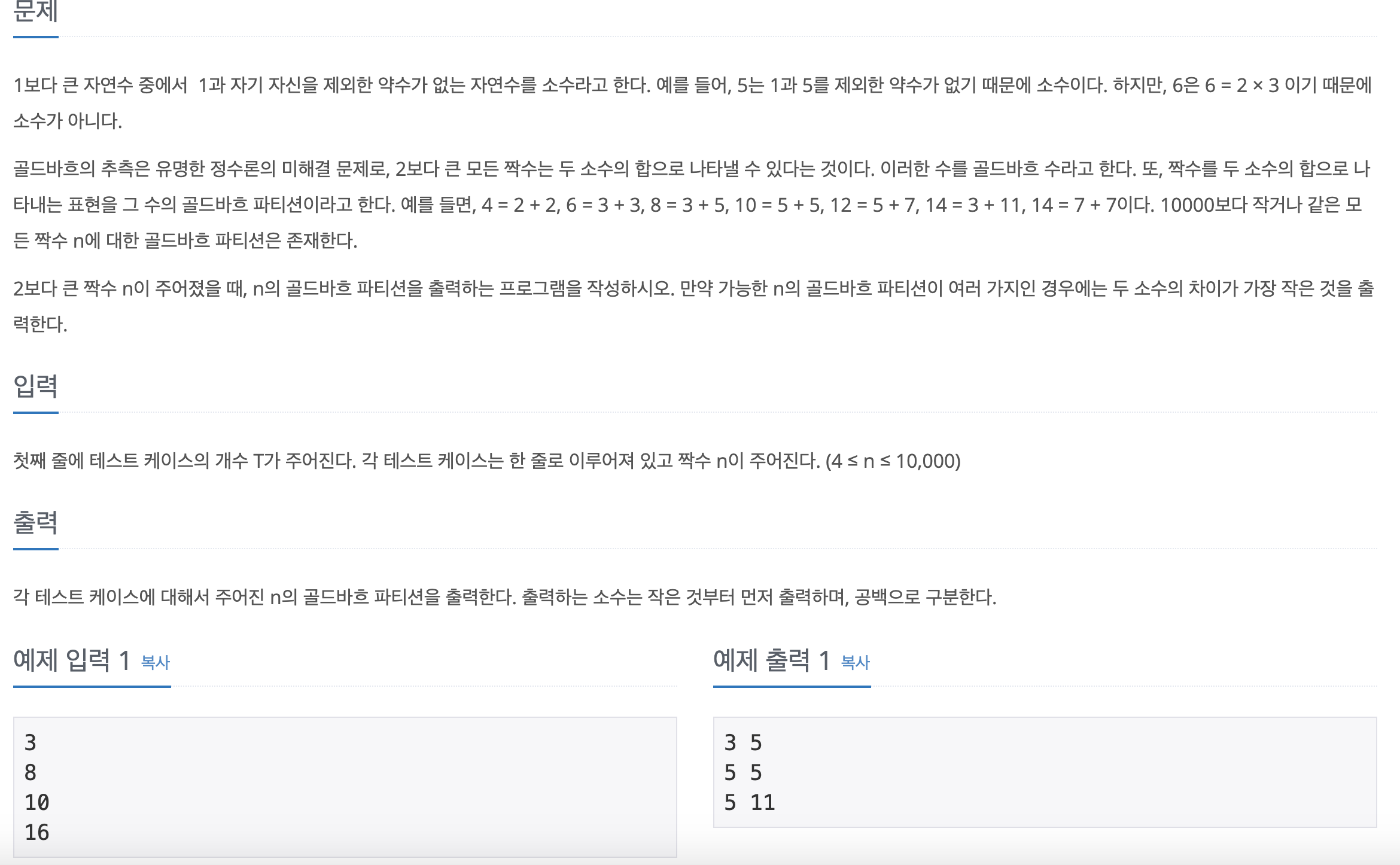
2보다 큰 모든 짝수는 두 개의 소수(Prime number)의 합으로 표시할 수 있다는 것이다. 이때 하나의 소수를 두 번 사용하는 것은 허용한다.
풀이방법
- 10000 이하의 소수를 모두 구하여 배열에 저장한다.(에라토스테네스의 체 사용)
- 가장 작은 소수는 2부터 시작이므로 2부터 시작하여 합이 N이 되는 2개의 소수를 찾는다.
for(int i=2; i<=num/2; i++) {
if(prime[i] == 0 && prime[num-i] == 0) {
min = i;
}
}
// 두 소수 : i , num-i두 소수의 합이 N(num)이 되는 것이므로 N(num)/2까지만 구하면 되고
이때, 숫자가 커질 수록 두 수의 차이가 작아지므로 i의 최대 값을 구한다.
소스코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
// 골드바흐의 추측
public class Main {
static final int prime[] = new int[10001];
public static void main(String[] args) throws Exception{
setPrime();
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int cnt = Integer.parseInt(br.readLine());
for(int i=0; i<cnt; i++) {
int sum = Integer.parseInt(br.readLine());
System.out.println(goldBach(sum));
}
}
public static String goldBach(int num) {
StringBuilder sb = new StringBuilder();
int min = 0;
// 숫자가 가까워 질 수록 차이는 최소가 된다.
for(int i=2; i<=num/2; i++) {
if(prime[i] == 0 && prime[num-i] == 0) {
min = i;
}
}
return sb.append(min).append(" ").append(num-min).toString();
}
// 에라토스테네스의 체
public static void setPrime() {
for(int i=2; i<=10000; i++) {
for(int j=i*i; j<=10000; j+=i) {
prime[j] = -1;
}
}
}
}