Big O 표현식 단순화하기
Big O 표기법 단순화는 모든 연산자들을 다 세는 것이 힘들고 정확한 갯수는 별로 중요하지 않다.
전체적인 추세를 중요하게 여긴다는 것이다.
5n+2라는 식을 그냥 n으로 단순화 할 수있다.
n이 커질수록 실행 시간도 비례하게 늘어나고 n 2든, n 9, n 10, n 100 크게 중요하지 않다 전부 n이다.
그래프에 선이 n의 값과 비례하다는 것이다.
이 식들을 단순화하기 위해 도움이될 규칙들에 대해서 알아보자.
단순화 규칙
가장 중요하게 생각하는 것은 반복해서 말하지만 큰 그림이다.
그렇기 때문에 상수는 중요하지 않다.
O(2n)이 있다면 이걸 O(n)으로 단순하게 표기할 수 있다.
O(500)이 있다면 이걸 그냥 O(1)이라고 한다. O(500)은 쉽게 말하면 연산 갯수가 어떤 상황이든 500개라는 말이기 때문이다.
그래프 선을 보면 납작하기 때문이다.(n의 갯수와 시간이 비례하지않다.)
O(13n2)이라면 상수는 필요 없기에 O(n2)이라고 한다.
O(2n) -> O(n)
O(500) -> O(1)
O(13n2) -> O(n2)
Big O의 복잡도를 분석할때 때론 매우 복잡해진다.
섬세하게 작은 내용들까지 따질 수도 있겠지만 쉽게 적용하는 규칙이 있다.
항상 맞는건 아니지만 좋은 시작점이 된다.
- 연산은 상수이다. 덧셈, 뺄셈, 곱셈, 나눗셈을 포함한다.
- 변수 선언도 상수이다.
- 인덱스를 사용해서 배열 엘리먼드를 접근하는것도 상수이다. 객체를 다루고 데이터를 접근하기 위한 키가 있다면 그것도 실행 시간이 상수이다.
- 루프가 있으면 복잡도가 루프의 길이 곱하기 루프안에 있는 연산자들이 된다.
function logAtLeast5(n) {
for (let i = 1; i <= Math.max(5, n); i++) {
console.log(i);
}
}logAtLeast5()는 루프가 있고 5까지 가거나 n까지 반복하는 함수이다.
물론 5를 신경쓸 수는 있지만 n이 작을 경우에만 적용되는 부분이고 우리가 주목해야할 점은 n이 더 커지고 커지는 경우이다.
만약 n이 1000만번이면 이 루프는 1000만번 반복될 것이다.
이 함수의 Big O를 O(n)이라고 단순화 할 수 있다.
function logAtMost5(n){
for (let i = i; i <= Math.min(5, n); i++) {
console.log(i);
}
}반대로 logAtMost5(n)함수는 30을 입력하면 5번 나오고 3을 입력하면 3번이 나온다. 5보다 더 큰 숫자를 입력하면 5번만 출력할 것이고, 5보다 더 작은 숫자를 입력하면 작은 숫자만큼 반복한다. 무슨 일이 있어도 5번 반복을 넘지는 않기 때문에 O(1)이 된다. O(5) 대신 O(1)으로 단수화 할 수 있는 것이다.
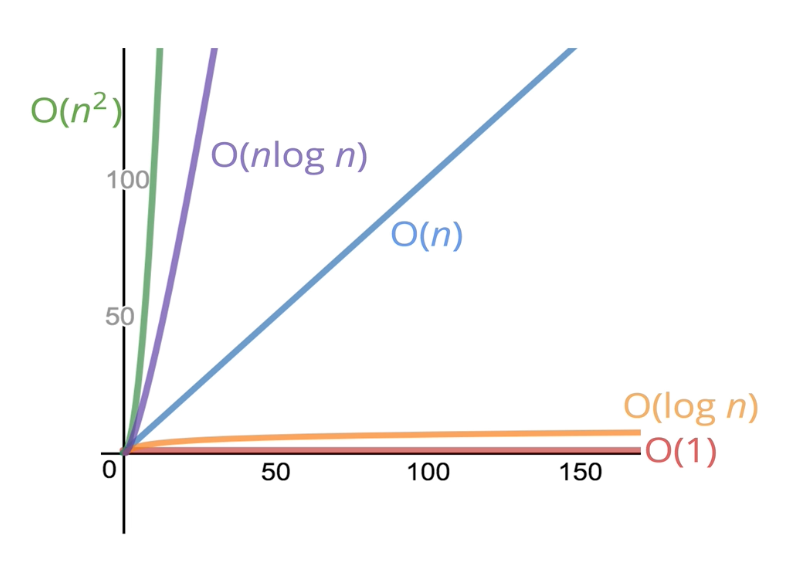
위의 그래프는 각 Big O 별 그래프의 그림이다.
아직 log n 이나 nlog n 배우지 않았지만 그래프만 본다면 O(n2)는 최대한 피해야 겠다는 생각을 하게된다.
