[알고리즘 문제 풀이][파이썬] 백준 10217번: KCM Travel

백준 10217 문제 링크: https://www.acmicpc.net/problem/10217

📑 문제 설명
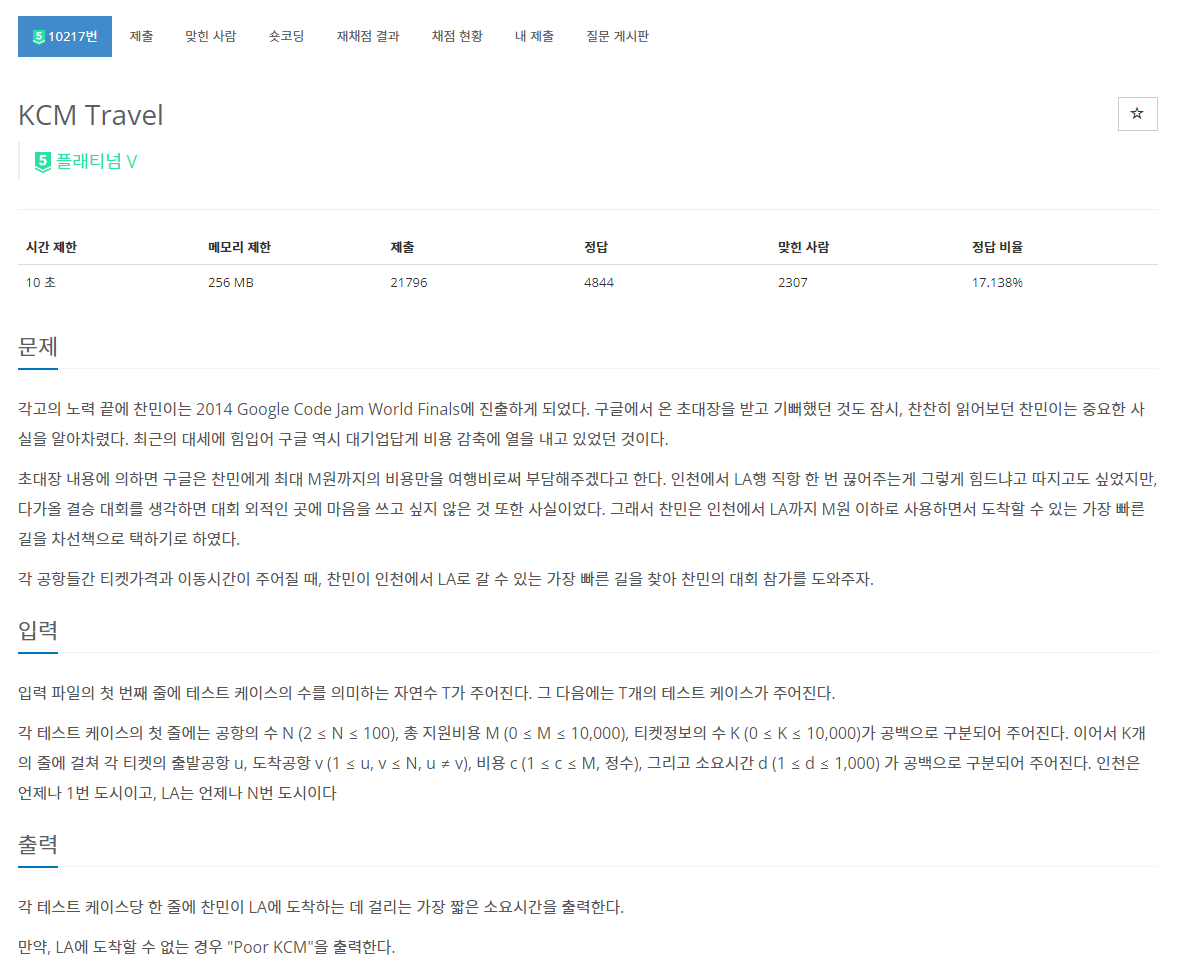
인천에서 LA까지 M원 이하로 사용하면서 도착할 수 있는 가장 빠른 길찾기

입력:
첫째줄 T:테스트 케이스 수
각 테스트 케이스 첫 줄: N, M, K - 공항의 수, 지원비용, 티켓정보의 수(edge)
각 테스트 케이스 두번째줄: u, v, c, d - 출발공항, 도착공항, 비용, 소요시간

• 인천은 1번 도시, LA는 N번 도시

출력:
각 테스트 케이스당 한 줄에 LA가 도착하는 데 걸리는 가장 짧은 소요시간 출력
LA에 도착할 수 없는 경우 "Poor KCM" 출력

💡 문제 해결 방법
Dijkstra algorithm

알고리즘 선택 이유
1. 방향 그래프 + 양수 가중치(multi weight) + 노드 그래프 --> Dijkstral algorithm

예외처리 및 추가 내용
1. 이 문제의 포인트는 M원 이하이기 때문에 1~M원까지 중 가장 짧은 dist를 찾아야 함
2. 따라서 2차원 테이블(행: 노드, 열: 0~m원까지의 cost)을 만들어야 함
- 하나의 노드를 방문했을 때 지금까지 합한 cost까지의 dist가 현재 테이블에 저장된 dist보다 작다면 지금까지 합한 cost~M원까지 합한 DIST로 치환해야함

스터디 내용
1. 비용을 고려하여 최단 시간 구하기
2. dist는 cost를 고려하는 dist --> (dist, cost) 형식으로 코딩

💻 코드

import sys
from collections import deque

def dijkstra():
    q = deque([(1, 0, 0)])
    dist_cost = [[1e10 for t in range(m+1)]for x in range(n+1)]
    dist_cost[1][0] = 0 # 시작노드 1의 cost(0)의 dist 업데이트
    while q:
        node, cost, dist = q.popleft()
        if dist_cost[node][cost] < dist:
            continue
        for nnode, ncost, ndist in graph[node]:
            temp_cost = cost + ncost
            temp_dist = dist_cost[node][cost] + ndist
            if temp_cost <= m and dist_cost[nnode][temp_cost] > temp_dist:
                q.append((nnode, temp_cost, temp_dist))
                for i in range(temp_cost, m+1):
                    if dist_cost[nnode][i] > temp_dist:
                        dist_cost[nnode][i]=temp_dist
                    else: break
    if dist_cost[n][m] == 1e10:
        print("Poor KCM")
        return
    print(dist_cost[n][m])


t = int(sys.stdin.readline())
for _ in range(t):
    n, m, k = map(int, sys.stdin.readline().split())
    graph = [[]for i in range(n+1)]
    for i in range(k):
        # u: 출발 공항, v: 도착 공항, c: 비용, d: 소요시간
        u, v, c, d = map(int, sys.stdin.readline().split())
        graph[u].append([v, c, d])

    dijkstra()

💟 추가적으로 알게 된 점
1. heapq로 구현해봤으나 시간초과 남 --> 시간 초과가 날 때는 deque로 변경하여 테스트 해보자
2. index 관리 잘하자
- 본인은 index 주어지는 cost가 0~10000인데, 2차원 테이블 만들 때 0~10000size의 배열을 만들고 초기화함. 그러나 누적되는 가격은 10000이 넘을 수 있음 --> 이런 사소한 예외사항을 고려할 것
참고
https://velog.io/@blucky8649/%EC%BD%94%ED%8B%80%EB%A6%B0-%EB%B0%B1%EC%A4%80-10217%EB%B2%88-KCM-Travel-%EB%AC%B8%EC%A0%9C%ED%92%80%EC%9D%B4