백준 11657 문제 링크: https://www.acmicpc.net/problem/11657
📑 문제 설명
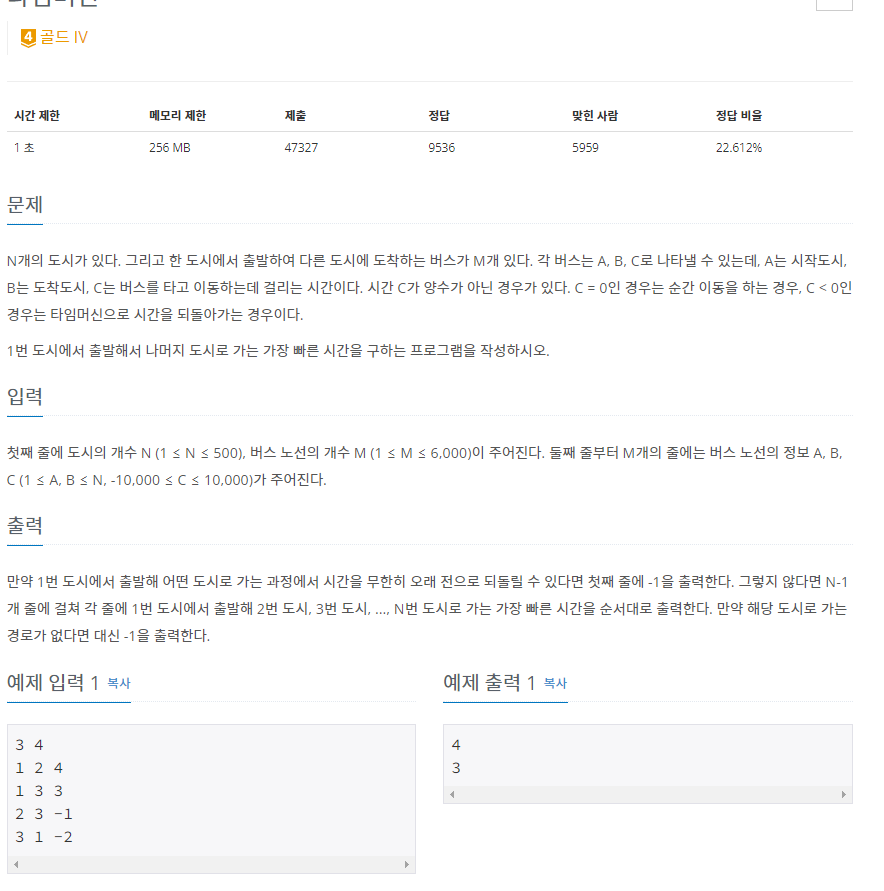
1. N개의 도시, 그리고 한 도시에서 출발하여 다른 도시에 도착하는 버스 M개 존재
2. A: 시작도시, B: 도착도시, C: 버스를 타고 이동하는데 걸리는 시간
* 단 C가 양수가 아닌 C = 0 인 경우는 순간 이동을 하는 경우이고, C < 0 인 경우는 타임머신으로 시간을 되돌아가는 경우
3. 1번 도시에서 출발하여 나머지 도시로 가는 가장 빠른 시간을 구하기
입력: 첫째 줄에 도시의 개수 N, 버스 노선의 개수 M이 주어지며 둘째줄부터 버스 노선의 정보 A, B, C가 주어진다.
출발지와 도착지는 같은데 시간이 다른 여러 개의 버스가 존재할 수 있음`
출력
1) 타임머신 버스를 계속 타게 되어 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다.
2) 시간을 무한히 오래 전으로 되돌릴 수 없다면 1번 도시에서 2번, 1번 도시에서 3번, ..., 1번 도시에서 N번까지 가는 가장 빠른 시간을 순서대로 출력한다. (N-1줄)
3) 1번에서 출발하여 해당 도시로 가는 경로가 없다면 -1을 출력한다.
💡 문제 해결 방법
알고리즘: 벨만 포드
1. 시작 정점을 결정한다.
2. 시작 정점에서 각각 다른 정점까지의 거리 값을 무한대로 초기화한다.
시작 정점은 0으로 초기화
timelist[0] = 0, timelist[0-->1] = INF
3. 현재 정점에서 모든 인접 정점들을 탐색하며, 기존에 저장되어 있는 인접 정점까지의 거리보다 현재 정점을 거쳐 인접 정점에 도달하는 거리가 더 짧을 경우 짧은 거리로 갱신
4. 3번의 과정을 V-1 번 반복한다.
5. 위 과정을 모두 마치고 난 후 거리가 갱신되는 경우가 생긴다면 그래프에 음수사이클이 존재한다는 것.
*출처: https://velog.io/@younge/Python-%EC%B5%9C%EB%8B%A8-%EA%B2%BD%EB%A1%9C-%EB%B2%A8%EB%A7%8C-%ED%8F%AC%EB%93%9CBellman-Ford-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
알고리즘 선택 이유
1. 도시가 버택스고 버스가 방향성과 가중치가 있는 edge를 의미
2. 일반 그래프 + 방향성 + 음수 가중치를 기반으로 최소시간을 출력 --> 벨만포드 알고리즘
음수 가중치가 있는 그래프에서 최단 거리를 얻고자 할 때 사용가능
음수사이클을 체크할 경우에는 먼저 V-1번 탐색을 해 준 후에 알고리즘을 한 번 더 돌렸을 때 값이 바뀐다면 음수사이클 존재
예외처리
1. 1번이랑 연결되어 있지 않고, 나머지 노드끼리 음수사이클이 발생한다면 출력 기준 1)이 출력됨. 따라서 1번을 거쳤는지 확인할 체크 리스트 필요
ex) 1/ 2--> <--3 일 경우, 출력은 -1/-1이 출력되어야 하지만 -1 한 번만 출력됨
2. INF를 생각보다 크게 설정해야 함 최소 1e10
스터디 내용
1. 그래프는 두 섬을 잇는 edge가 2개 이상인 multiple graph
2. 벨만 포드 돌리면 답이 나옴
3. 벨만 포드를 사용하는 첫 번째 문제
💻 코드
import sys
n, m = map(int, sys.stdin.readline().split())
graph = [[-1]] + [[] for x in range(n)]
visit = [-1] + [1e10 for x in range(n)]
for i in range(m):
a, b, c = map(int, sys.stdin.readline().split())
graph[a].append([b,c])
def bellmanford():
if len(graph[1]) == 0:
for i in range(2, n+1):
print(-1)
return
visit[1] = 0
for i in range(n-1):
for node in range(1, n+1):
for b, c in graph[node]:
visit[b] = min(visit[b], visit[node]+c)
for node in range(1, n+1):
for b, c in graph[node]:
if visit[b] > visit[node] + c:
print(-1)
return
for i in range(2, n+1):
if visit[i] == 1e10:
print(-1)
else:
print(visit[i])
bellmanford()
💟 추가적으로 알게 된 점
1. 벨만 포드 알고리즘 자체를 공부할 수 있었던 문제
2. 구현 자체는 어렵지 않으나 자꾸 탐색을 하는 방법으로 bfs나 dfs를 쓰려고 하는 습관 때문에 오히려 시간이 더 걸렸음
3. 방향이 존재하고 음수 가중치가 존재한다면 벨만 포드 알고리즘을 잊지 말것

