[Optimization] First-order vs Second-order Method

YEOM JINSEOP·2024년 7월 18일

Quantization[이론]

목록 보기
2/2

First-order method

(1계 도함수법)

  • Linear approximation using gradients

Second-order method

(2계 도함수법)

  • Quadratic approximation using Hessians

  • Second-order methods typically provide more accurate approximations.

  • However, The practical performance of each method depends on factors such as problem size, computational resources, and numerical stability

Hessian matrix H\bold{H}

f(x1,x2,...,xn)f(x_1, x_2, ..., x_n) 일 때,


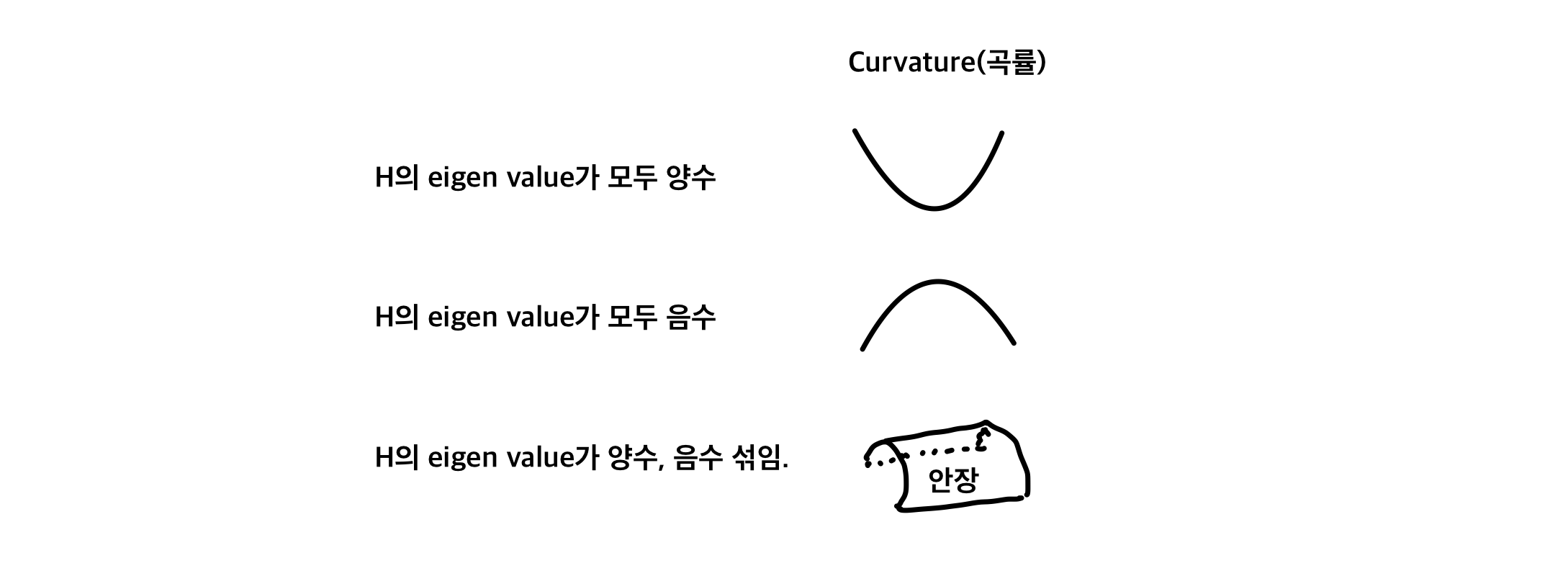
H\bold{H}의 eigen value는 ff의 curvature(얼마나 휘었는지)를 결정한다.
λ\lambda가 크면, 많이 휘었다.

그래서 Newton's method에서

wnew=w−∇f(w)H\bold{w}^{new} = \bold{w} - \frac{\nabla{f(\bold{w})}}{\bold{H}}

curvature가 큰 방향(많이 휜 방향)으로는 작은 step을,
curvature가 작은 방향으로는 큰 step을 취한다.
즉, 함수의 local geometry를 고려한 최적의 방향과 크기로 update한다.

1차원 newton's method

xn+1=xn−f(xn)f′(xn)x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

2차원 newton's method

  • Taylor 급수로 2차원 근사
    f(x+Δx)≈f(x)+∇f(x)TΔx+12ΔxTHΔxf(x + \Delta x) \approx f(x) + \nabla{f(x)^T}\Delta{x} + \frac{1}{2}\Delta{x^T}H\Delta{x}
    ∂f∂Δx=∇f(x)+HΔx=0\frac{\partial{f}}{\partial{\Delta{x}}} = \nabla{f(x) + H\Delta{x} = 0}
    ∴Δx=−∇f(x)H\therefore \Delta{x} = - \frac{\nabla{f(x)}}{H}

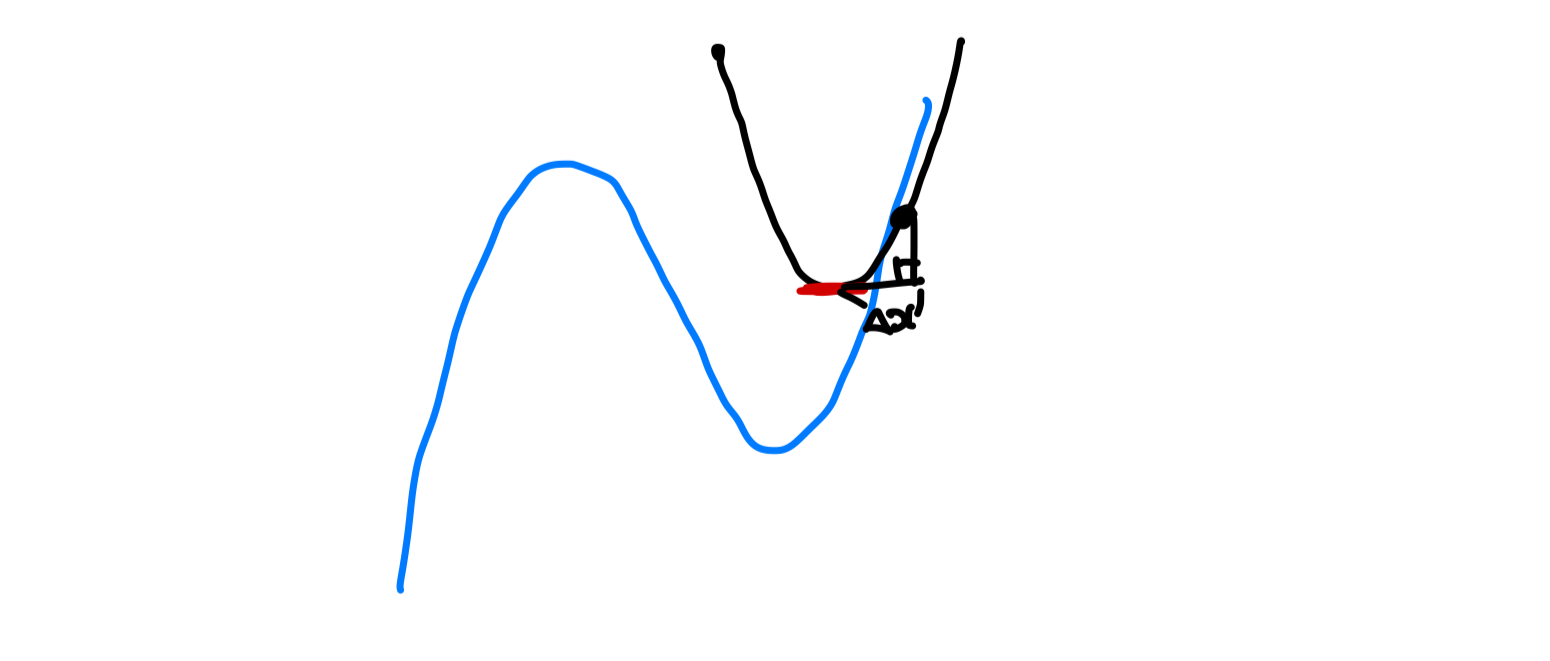
Newton's method

뉴턴법 알고리즘
\\
STEP 1. 초기값 x(0)\bold{x}^{(0)}을 정한다. k=0k=0
STEP 2. ∣∣∇f(x(k))∣∣||\nabla f(\bold{x}^{(k)})||가 충분히 작다면 종료한다.
STEP 3. x(k+1)=x(k)−∇f(x(k))∇2f(x(k))=x(k)−∇f(x(k))H\bold{x}^{(k+1)}= \bold{x}^{(k)}-\frac{\nabla{f(\bold{x}^{(k)})}} {\nabla^2 f(\bold{x}^{(k)})} = \bold{x}^{(k)}- \frac{\nabla{f(\bold{x}^{(k)})}}{\bold{H}} , where H\bold{H} = Hessian matrix

\\

아래 그림의 왼쪽은 objective function을 1차 근사할 경우를, 오른쪽은 2차 근사할 경우를 나타낸다.

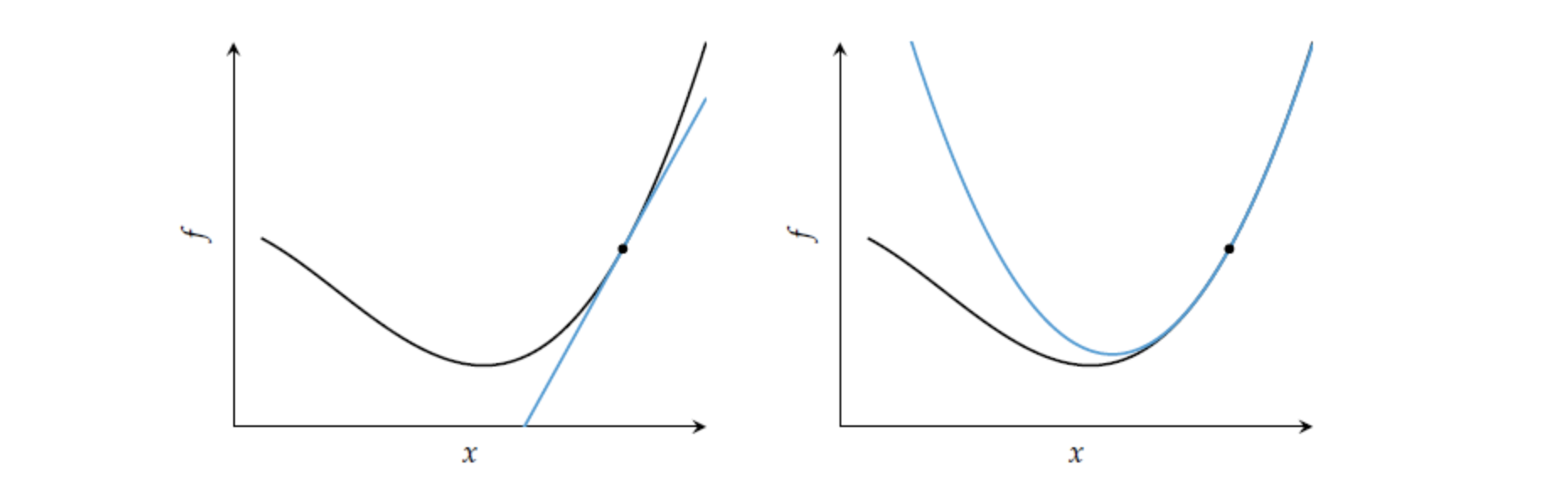
  • first-order method에서 gradient는 최적해로 향하는 방향은 알려주지만, 얼만큼 이동해야 할지 step-size는 알려주지 못하기에, 다양한 방법을 통해 적절한 step-size를 조절하려고 했다.
    \\
    반면, second-order 정보는 목적함수의 2차 근사를 가능하게 하고, 최적해 혹은 local minima에 도달할 수 있는 스텝의 크기 역시 근사할 수 있다.

  • 왼쪽 그림(first-order method)을 살펴보면 1차 근사로는 얼마나 이동해야하는지 알 수 없지만,
    \\
    오른쪽 그림(second method)을 살펴보면 2차 근사에서 구할 수 있는 최소값이 최적해 근처에 위치할 것을 알 수 있다.

  • 목적함수 f(x)f(x)에 대해 테일러 전개를 이용하면 2차 근사식 q(x)q(x)는 다음과 같이 구해질 것이다.
    \\

    q(x)=f(xk)+(x−xk)f′(x)+(x−xk)22f′′(xk)q(x) = f(x_k) + (x-x_k)f'(x) + \frac{(x-x_k)^2}{2}f''(x_k)

    \\
    이때 2차 함수의 최소값을 구하기 위해 미분을 이용하면 다음과 같다.

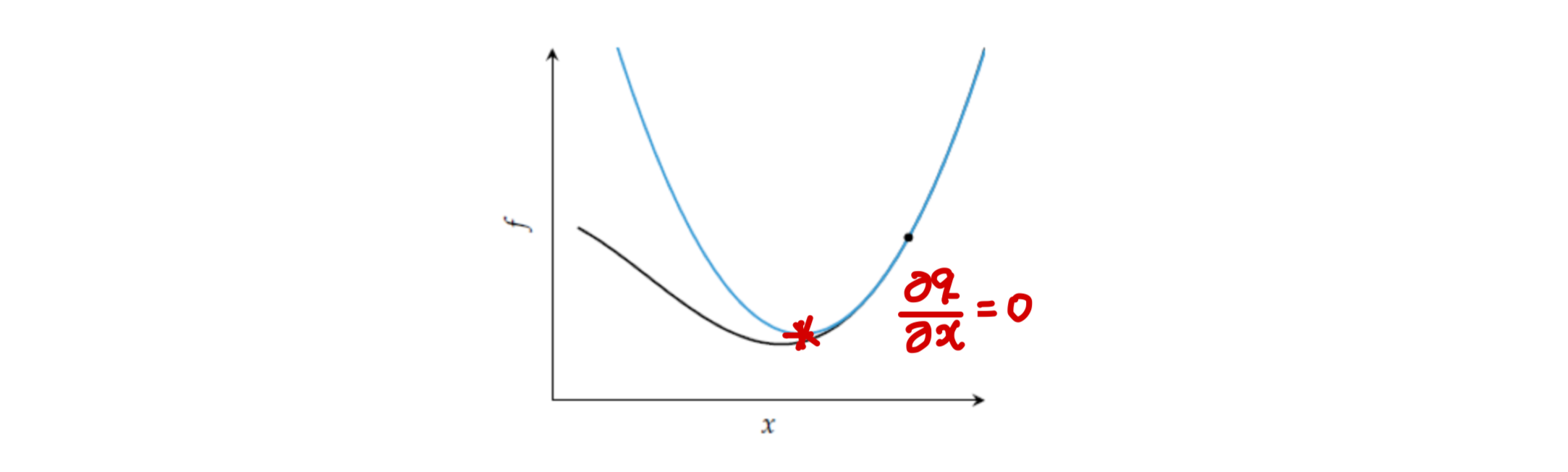
    ∂q∂x=f′(x)+(x−xk)f′′(x)=0\frac{\partial{q}}{\partial{x}} = f'(x) + (x-x_k)f''(x) = 0

    \\

    x−xk=−f′(x)f′′(x)x -x_k= -\frac{f'(x)}{f''(x)}

    \\

    ∴x=xk−f′(x)f′′(x)\therefore x = x_k-\frac{f'(x)}{f''(x)}

    \\
    즉, first-order method와 달리 뉴턴번은 2차 근사한 식의 최소점으로 이동함으로써 가중치들을 업데이트하게 된다.
    이는 방향과 스텝의 크기가 분리되지 않고, 함께 계산되는 모습을 보여준다.
    결국 뉴턴법의 업데이트 방식은 아래 식으로 정리할 수 있다.
    \\

    xk+1=xk−f′(x)f′′(x)x_{k+1}=x_{k}-\frac{f'(x)}{f''(x)}

    \\

  • 하지만 뉴턴법은 2차 도함수를 분모로 가지고 있기 때문에, 2차 미분이 0이 되면 업데이트를 할 수 없다. 이는 국소적으로 수평선인 경우에 발생하게 되는데, 2차 미분이 0에 가깝더라도 문제가 발생한다. 2차 미분의 값이 매우 작기 때문에 업데이트가 멀리 일어나게 되고, overshoot이 발생할 수 있다. 이는 아래 그림과 같이 근사식의 최소값이 최적해로부터 멀리 떨어져 있을 경우에 발생하게 된다.

다변수 함수에서의 뉴턴법

지금까지 일변수 함수에서의 뉴턴법을 살펴보았는데, 이를 다변수 함수로 확장하면 다음과 같다.
xk\bold{x}_k에서 다변수 2차 테일러 전개는 다음과 같다. 이때 HkH_k는 Hessian matrix를 의미한다.

f(x)≈q(x)=f(xk)+∇f(xk)T(x−xk)+12(x−xk)THk(x−xk)f(\bold{x}) \approx q(\bold{x}) = f(\bold{x}_k) + \nabla{f(\bold{x}_k)}^T(\bold{x} - \bold{x_k}) + \frac{1}{2}(\bold{x} - \bold{x}_k)^T \bold{H}_k (\bold{x} - \bold{x}_k)

위의 식에 대해 동일하게 gradient를 0으로 설정하면 다음과 같은 업데이트 식을 얻게 된다.

∇q(x)=∇f(xk)T+Hk(x−xk)=0\nabla{q(\bold{x})} = \nabla{f(\bold{x}_k)}^T + \bold{H}_k(\bold{x} - \bold{x}_k) = 0

\\

xk+1=xk−(Hk)−1∇f(xk)T\bold{x}_{k+1} = \bold{x}_k - (\bold{H}_k)^{-1}\nabla{f(\bold{x}_k)}^T

참고 자료
제대로 배우는 수학적 최적화(지은이 우메타니 슌지)
jaeheekim님 Velog 포스팅: 8. 2계 도함수법

profile
YEOM JINSEOP

0개의 댓글