Motivation

• fine-tuning은 all the parameters of the pre-trained model을 update한다.

• large model을 pre-train하기에, 모든 model parameter들을 retraining하는 full fine-tuning은 less feasible해지고 있다.

• GPT-3 175B를 예로 들면, 각 175B parameter의 independent한 fine-tunde model의 instance를 deploy하는 것은 매우매우매우 비싸다.

• 많은 이전의 연구들은, new task를위해,
  약간의 parameter를 adapting하거나,
  external modules를 learning하는 방법을 사용했다.

  • 장점
    • 이 방법은 적은 수의 task-specific parameters만 store하고 load하면 되기에, efficient하다.
  • 단점
    • 하지만, inference latency를 늘린다.
      • model depth를 키우거나 model의 usable sequence length를 줄이기 때문.
      • efficiency와 module quality 간의 trade-off 가짐.

• inspiration

  • 학습된 over-parametrized 모델들이 실제로 낮은 intrinsic dimension에 위치한다는 것을 보인 연구를 토대로,

    • 1. Measuring the Intrinsic Dimension of Objective Landscapes
    • 2. Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning

  • model adaptation 과정에서 발생하는 weight 변화 또한 낮은 "intrinsic rank"를 가질 것이라고 가설을 세움.

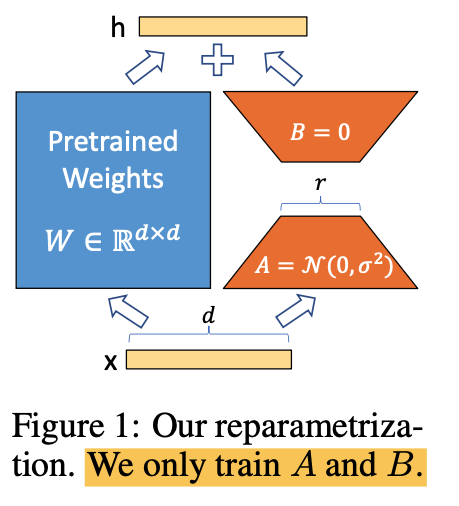
  • LoRA를 사용하면 neural network의 일부 dense layer들을 indirect하게 학습 가능.

    • pre-trained weight들을 frozen 상태로 유지하면서,

    • adaptation 과정에서 dense layer의 변화를 rank decomposition matrix(low-rank matrix)들을 optimize하는 방식

    • 

Apporach

• LoRA는 pretrained model weight를 freeze하고,
  trainalbe rank decomposition matrices를 각 Transformer의 layer에 inject한다.
  ➡️ downstream task를 위한 trainable parameter 개수를 크게 줄임.

  • Adam으로 fine-tuned된 GPT-3 175B와 비교해서,
    trainable paramter를 10,000배 줄이고
    GPU memory requirment를 3배 줄임.

  • no additional inference latency

Problem Statement (Full fine-tuning)

• full-fine tuning 과정에 대해 살펴 보면,

• pre-trained (auto-regresive) language model $P_\Phi(y|x)$는 parametrized by $\Phi$

• Each downstream task는
  training dataset of context-target pairs:$\mathcal{Z} = \{(x_i, y_i)\}_{i=1,...,N}$ 으로 표현됨.

  • $x_i$ : sequence of tokens,
    $y_i$: sequence of tokens

    $\\$

  • ex) in NL2SQL,
    $x_i$: natural language query
    $y_i$: corresponding SQL commdands

  • ex) for summarization,
    $x_i$: content of article
    $y_i$: its summary

• full-finetuning 동안,

  • model은 pre-trained weight $\Phi_0$로 intialized.

  • 그리고 $\Phi_0 + \Delta\Phi$ 로 updated됨.

    • 아래 conditional LM objective를 maximize하도록, 반복적으로 gradient를 따라 update됨.
    • 

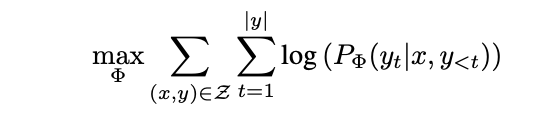
• full-finetuing의 main drawback

  • 각 downstream task에 대해, 각기 다른 parameter set $\Delta\Phi$을 학습해야 한다는 점.

  • $\text{dim}(\Delta\Phi) = \text{dim}(\Phi_0)$

  • 따라서, pre-trained model이 크다면, 각 independent한 fined-tuned model들의 instance를 stroing하고 deploy하는 것은 challenging 함.

• LoRA

  • parameter-efficient approach

  • task-specific parameter incerement $\Delta{\Phi} = \Delta\Phi({\Theta})$는 low-rank representation을 사용해서,
    훨씬 작은 parameters set $\Theta$로 encode한다.

  • $\text{dim}(\Theta) << \text{dim}(\Phi_0)$

  • $\Delta{\Phi}$를 찾는 task에서,
    $\Theta$를 optimize하는 task로 바뀜.

  • 

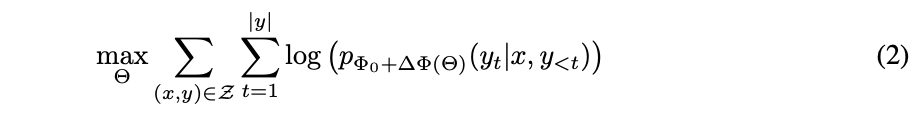
기존 Solution들의 한계

• efficient adaptation의 두 가지 주요 전략

  • 1.adapter layers 추가
  • 2.input layer activation들의 form을 optimize(prompt optimize)

• 1.Adapter Layers

  • 각 Transformer block마다 두 개의 adapter layer를 추가하거나,
    adapter layer와 추가적인 LayerNorm 사용하는 연구 등.

  • 단점: 매우 작은 bottleneck dimension을 사용하더라도 adapter를 사용할 때 latency가 눈에 띄게 증가

    • sequential하게 adapter layers가 processed돼야 하기 때문.

• 2.Optimizing the Prompt

• 대표적인 예인 Prefix tuning은 optimize하기 어려움.

• trainable parameter 수에 따른 성능 변화가 예측 불가능함.

• adaptation을 위해 sequence length의 일부를 사용함으로써 downstream task를 위한 유효 sequence length가 줄어드는 trade-off가 존재.

Method

Low-rank parametrized update matrices

• layer의 weight matrix들은 주로 full-rank를 갖는다.

• Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning(Aghajanyan et al, 2020) 연구는
  $\\$
  specific task에 adapting할 때, pre-trained language model들이 낮은 "intrinsic dimension"을 가지고 있으며,
  $\\$
  smaller subspace로의 random projection에도 불구하고 여전히 efficient하게 learning 할 수 있다는 것을 보임.

  • claude 3.5 설명 첨부
    • Intrinsic dimension은 pre-trained language model의 parameter 공간에서 실제로 중요한 변화가 일어나는 차원의 수를 의미함.
    • 대규모 language model이 겉보기에는 매우 많은 parameter를 가지고 있지만, 실제로는 훨씬 더 작은 차원의 subspace에서 대부분의 중요한 learning과 adaptation이 일어난다는 것을 시사함.

• 위 연구에 inspired 받아,
  저자는 adaptation 동안 weight에 대한 update도 낮은 "intrinsic rank"를 가질 것이라고 hypothesize함.

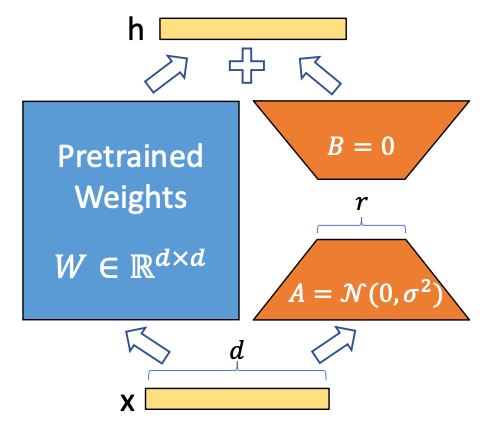
• pre-trained weight matrix $W_0 \in \mathbb{R}^{d \times k}$에 대해,
  $W_0$의 update $\Delta{W}$를 low-rank decomposition로 제한한다(constrain)

  $W_0 + \Delta{W} = W_0 + BA$

  where $B \in \mathbb{R}^{d \times r}$, $A \in \mathbb{R}{r \times k}$,
  rank $r << \text{min}(d,k)$

• training 동안,

  • $W_0$는 frozen ❄️. graident updates ❌
  • $A$와 $B$는 trainable parameters를 가짐.
  • $W_0$와 $\Delta{W} = BA$는 동일한 input에 곱해지고,
    각각의 output vector들은 coordinate-wise로 sum한다.
  • $h = W_0x$에 대해, LoRA forward pass는
    $h = W_0x + \Delta{W}x = W_0x + BAx$
  • 
    • training 시작 시에,
      • $A$는 random Gaussian initialization을 사용
      • $B$는 zero
      • $\therefore$ $\Delta{W} = BA$는 zero로 시작.

• $\Delta{W}x$를 $\frac{\alpha}{r}$로 scaling

  • $\alpha$는 고정된 상수(constant)이고, $r$은 rank
  • $\frac{\alpha}{r}$로 scaling함으로써, $r$이 변할 때 전체 update의 크기가 크게 변하지 않도록.
  • 즉, low-rank 업데이트의 크기를 조절하는 역할.
  • Adam optimizer와의 관계
    • Adam에서는 learning rate가 update의 크기를 조절
    • $\frac{\alpha}{r}$로 scaling하는 것은 실질적으로 learning rate를 조절하는 효과.
    • 이러한 방식으로 $\alpha$를 설정하면, $r$을 변경할 때마다 learning rate나 다른 hyperparameter를 재조정할 필요가 줄어듦.

• 

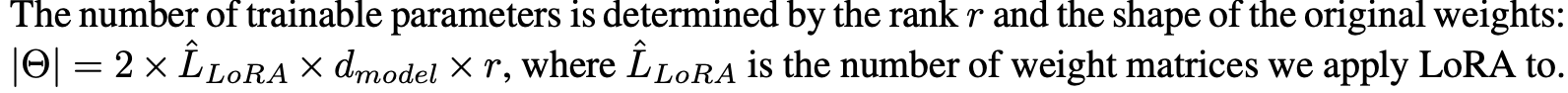
No Additional Inference Latency

• Production 환경에 deploy할 때, $W = W_0 + BA$를 계산하고 저장하여 일반적인 방식으로 inference를 수행 가능.
• $W_0$와 $BA$ 모두 $\mathbb{R}^{d \times k}$ dimension임에 주목.
• 다른 downstream task로 전환해야 할 때, $BA$를 빼고 다른 $B'A'$를 사용하면 됨.
  • 이는 매우 적은 memory overhead로 빠르게 수행할 수 있는 연산.
  • inference 동안 어떠한 추가적인 latency도 발생시키지 않음을 보장.

Applying LoRA to Transformer

• LoRA는 어떤 weight matrix들의 subset에도 적용해서, trainable parameter를 줄일 수 있음.

• Tranformer 구조에선, self-attention module에 4개의 weight matrix들 ($W_q, W_k, W_v, W_o$)과 MLP module에 2개의 matrix가 존재.

• LoRA는 $W_q$ (또는 $W_k, W_v$)를 $d_{model} \times d_{model}$ dimension의 single matrix로 취급함.
  이는 output dimension이 일반적으로 attention head들로 나눠지더라도 마찬가지.

• simplicity와 parameter-efficiency를 위해 downstream task에서
  attention weight 🔥만을 adapt하고 MLP module은 freeze ❄️
  (즉, MLP module은 training되지 않음)

• MLP layers, LayerNorm layers, 나머지 parameter들의 adapting에 관한 empirical investigation은 future work로 남김.

Praticial Benefit & Limitation

• Benefit

  • memory와 storage usage의 reduction

  • Adam으로 train된 large Transformer의 경우, $r ≪ d_{model}$이면 frozen parameter에 대한 optimizer state를 store할 필요가 없음
    ➡️ VRAM usage $\frac{2}{3}$까지 감소

    • r은 LoRA의 rank를, $d_{model}$은 원래 모델의 dimension을 나타냄.
    • r이 $d_{model}$보다 훨씬 작다는 것은 학습해야 할 parameter 수가 크게 줄어든다는 의미.
    • Adam은 각 parameter에 대해 first moment(평균)와 second moment(분산) 등의 state를 유지.
    • 이 state들은 각 parameter마다 저장되어야 하므로, parameter 수만큼의 추가 memory가 필요.
    • Frozen parameter는 update되지 않으므로, 이에 대한 optimizer state를 유지할 필요가 없음.
    • LoRA에서는 대부분의 원래 parameter가 frozen 상태이므로, 이에 대한 optimizer state를 store할 필요가 없음.

  • r = 4이고 query와 value projection matrix만 adapt할 경우,
    ➡️ checkpoint size가 약 10,000배 감소(350GB에서 35MB로).
    ➡️ 훨씬 적은 수의 GPU로 train할 수 있고 I/O bottleneck을 피할 수 있음.

  • LoRA가 전체 model weight를 저장하지 않고, 작은 rank의 update만을 저장하기 때문에 가능

  • 또한 모든 layer가 아닌 query와 value projection matrix만 adapt하는 것도 size 감소에 기여

  • deployed 상태에서 모든 parameter가 아닌 LoRA weight만 swap함으로써 훨씬 낮은 cost로 task를 switch 가능.

• limitation

  • 각 input마다 다른 weight: $W = W_0 + BA$를 사용해야 하므로,
    기존의 batch matrix multiplication을 직접 적용할 수 없음.

  • 이로 인해, 단일 task에 대한 inference는 빨라지지만,
    여러 task의 input을 동시에 효율적으로 처리하는 것은 복잡해짐.
    

Understanding the Low-rank updates

• empirical studies to answer the follwing questions

• 1) Given a parameter budget constraint, which subset of weight matrices in a pre-trained Transformer should we adapt to maximize downstream performance?

  • Limited parameter budget (18M, 약 35MB)에서 어떤 weight를 adapt해야 downstream task에서 최고의 성능을 얻을 수 있는지 조사.

  • Self-attention module의 weight matrix만 고려.

  • 

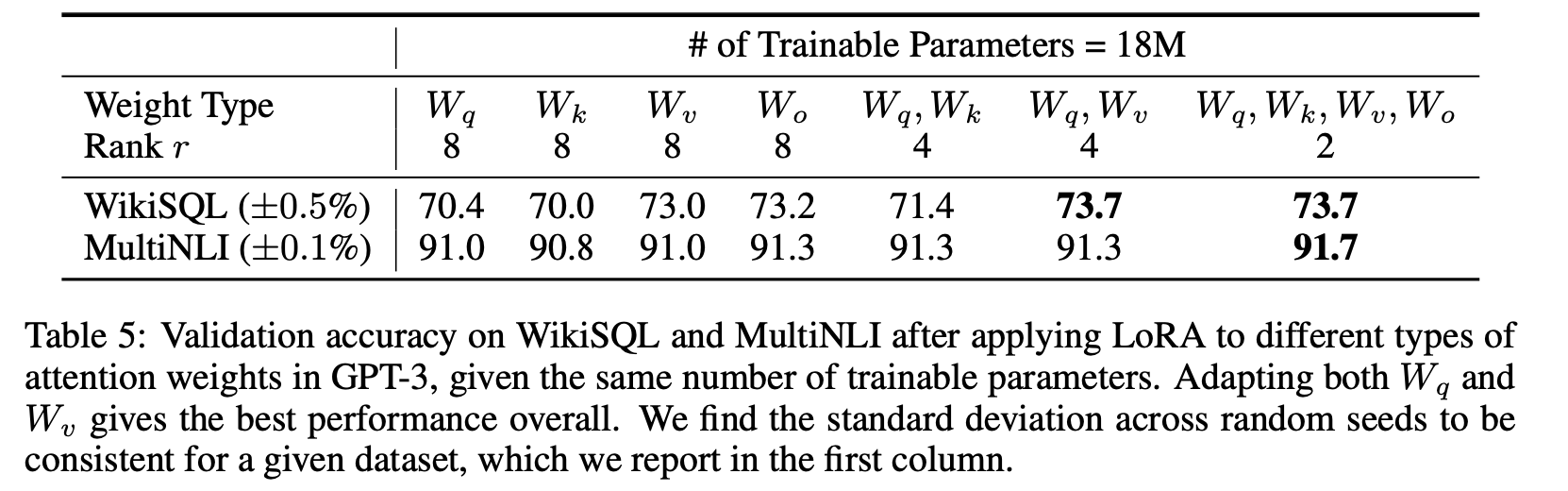
    • 실험 결과
      • Wq나 Wk만 adapt ➡️ 성능이 상대적으로 낮음.
      • Wq와 Wv를 함께 adapt ➡️ 가장 좋은 성능.
      • 모든 attention weight (Wq, Wk, Wv, Wo)를 함께 adapt하는 것도 좋은 성능을 보이지만,
        parameter 효율성 측면에서는 Wq와 Wv만 adapt하는 것이 더 효과적

  • 주요 발견

    • rank가 4로 낮아도 $\Delta{W}$의 충분한 information을 capture 가능.

    • 단일 type의 weight를 높은 rank로 adapt하는 것보다 여러 weight matrix를 낮은 rank로 adapt하는 것이 더 효과적.

• 2) Is the "optimal" adaptation matrix $\Delta{W}$ really rank-deficient?
  If so, what is a good rank to use in practice?

  • 

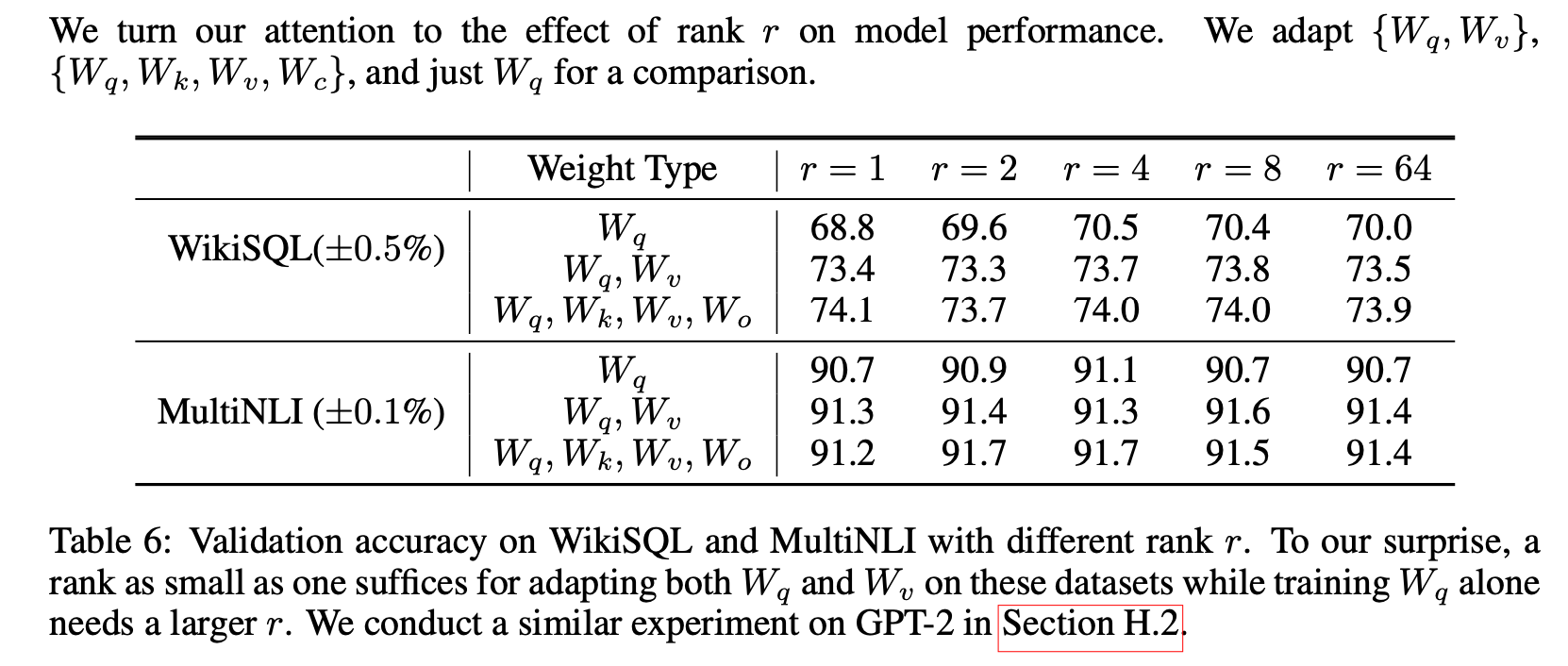
    • Table 6은 놀랍게도 LoRA가 매우 작은 $r$로도 이미 competitive한 performance를 보인다는 것을 보여줌
      (Wq만 adapt하는 것보다 {Wq,Wv}에서 더 좋음).

    • 이는 update matrix $∆W$가 매우 작은 "intrinsic rank"를 가질 수 있음을 suggest함.

    • 이 finding을 further support하기 위해, 서로 다른 $r$ 값과 다른 random seed에 의해 학습된 subspace들의 overlap을 check.

    • r을 증가시키는 것이 더 meaningful한 subspace를 cover하지 않는다고 주장,
      이는 low-rank adaptation matrix가 sufficient하다는 것을 suggest.

  • subspace similarity between different $r$

    • rank $r$이 다른 두 adaptation matrix 간의 subspace similarity를 분석.

      • 구체적으로는, $r = 8$과 $r = 64$의 adaptation matrix 사이에 어떤 singular vector가 얼마나 겹치는지를 조사

      • 이를 위해 두 rank에 대한 singular value decomposition을 수행하고, right-singular unitary matrices $U_{A_r=8}$와 $U_{A_r=64}$의 similarity를 비교함.

      • 이 유사성을 측정하기 위해, Grassmann distance 기반의 정규화된 subspace similarity를 사용.

      • $r = 8$에서 상위 $i$개의 singular vectors가 $r = 64$에서 상위 $j$개의 singular vectors와 얼마나 겹치는지를 평가

    • ⭐ 실험 결과

      • $r = 8$과 $r = 64$에서 상위 singular vector directions는 상당히 겹치지만, 나머지 방향들은 그렇지 않다는 점을 발견

      • 즉, r이 작은 경우에도 상위 singular vectors는 중요한 정보를 담고 있으며,
        $rank r = 1$ 조차도 다운스트림 작업에서 효과적인 이유를 설명 가능.

      • $r$이 커질수록 유용한 정보는 증가하지만,
        많은 singular directions는 noise에 가깝다는 결론에 도달

    • 이 분석은 LoRA의 adaptation matrix가 매우 낮은 rank에서도 유용한 정보를 충분히 캡처할 수 있다는 것을 강조.

  • Subspace similarity between different random seeds

    • random seeds를 다르게 설정한 두 번의 rank r = 64로 학습한 결과들 간의 subspace similarity를 분석.

    • 이를 통해, 동일한 rank r = 64로 학습했을 때, ∆Wq와 ∆Wv의 차이점을 관찰 가능.

    • 실험 결과

      • ∆Wq는 ∆Wv보다 더 높은 "intrinsic rank"를 가지고 있는 것으로 나타남.

        • 이는 ∆Wq가 두 random seeds 간에 더 많은 공통적인 singular value directions를 학습했다는 의미.
        • 이러한 결과는 Table 6에서 관찰된 실험적 결과와 일치하며, ∆Wq의 rank가 ∆Wv보다 상대적으로 더 높다는 것.

      • 또한, 두 개의 random Gaussian matrices를 비교했을 때,
        이들 사이에는 공통된 singular value directions가 거의 없다는 사실이 도출됨.

        • 이는 random Gaussian matrices 간의 subspace similarity가 매우 낮다는 것.

      • 이 실험을 통해, ∆Wq가 ∆Wv보다 더 중요한 singular directions를 학습하며,
        rank가 높을수록 유의미한 sub-space가 더 잘 포착된다는 것을 확인.

• 3) What is the connection between $\Delta{W}$ and $W$?
  Does $\Delta{W}$ highly correlate with $W$?
  How large is $\Delta{W}$ comparing to $W$?

  • ∆W가 W와 얼마나 높은 상관관계를 가지는지
    그리고 ∆W가 W의 상위 singular directions에 주로 포함되는지를 조사
  • Frobenius norm을 사용해 Wq의 subspace에 투영된 ∆Wq와 Wq를 비교하는 방식.
  • 
  • 실험 결과
    • ∆W는 W와 무작위 행렬(random matrix)과 비교했을 때 더 높은 상관관계를 가지며,
      ∆W는 W에 이미 존재하는 일부 특성을 증폭(amplify)하는 역할을 한다는 사실을 발견
    • 또한, ∆W는 W의 상위 singular directions를 반복하는 것이
      아니라 W에서 강조되지 않은 방향들만 증폭한다는 점을 발견
    • r = 4인 경우 amplification factor가 21.5에 달하는데, 이는 ∆Wq가 Wq의 특정 중요한 특성들을 매우 크게 증폭함을 나타냄.

Future Works

• LoRA는 다른 효율적인 적응 방법과 결합될 수 있으며, 이로 인해 orthogonal improvement(서로 독립적인 성능 향상)을 이끌어낼 가능성.

• LoRA 또는 fine-tuning의 메커니즘은 아직 명확하지 않음.
  pre-trianing 중에 학습된 특성들이 어떻게 downstream task에 잘 적용되는지에 대한 이해가 부족.
  LoRA는 full fine-tuning보다 이러한 질문에 답을 제시하는 데 더 효과적일 것으로 보임.

• 현재는 LoRA를 적용할 weight matrices를 선택하는 데 있어 주로 경험적인 방법(heuristics)에 의존.
  이를 더 원칙적인 방법으로 개선할 수 있는지에 대한 연구 필요.

• ∆W의 rank-deficiency는 W 또한 rank-deficient 할 수 있다는 점을 시사.