개요

백준 1373번 문제를 풀면서 2진수 문자열을 3개씩 쪼개고 8진수로 연산후에 합치는 과정을 배열을 다루면서 해결해보려고 시도했다.

function solution(sum) {
  let binary2 = sum;
  let binary8 = [];
  while (binary2.length >= 3) {
    binary8.unshift(parseInt(binary2.slice(binary2.length - 3), 2).toString(8));
    binary2 = binary2.slice(0, binary2.length - 3);
  }
  binary8.unshift(binary2 ? parseInt(binary2, 2).toString(8) : "");
  return binary8.join("");
}

결과는 시간초과였다. 답안을 찾아보면서 같은 풀이로 문자열로 풀은 답이 있길래 적용해봤더니 잘되었다.

function solution(sum) {
  let binary2 = sum;
  let binary8 = "";
  while (binary2.length >= 3) {
    binary8 =
      parseInt(binary2.slice(binary2.length - 3), 2).toString(8) + binary8;
    binary2 = binary2.slice(0, binary2.length - 3);
  }
  return (binary2 ? parseInt(binary2, 2).toString(8) : "") + binary8;
}

이럴때 제일 난감하다... 그냥 동작만 하면 안되나?? 라는 패배자 마인드가 생긴 기념, 둘의 동작방식을 파악해보도록 하겠다.

문자열은 원시타입, 배열은 참조타입

문자열은 숫자, 불리언, 심볼, null, undefined과 함께 원시타입이다. 자바스크립트의 배열은 엄밀히 말해 일반적 의미의 배열이 아니다. 자바스크립트의 배열은 일반적인 배열의 동작을 흉내낸 특수한 객체이다. 객체는 참조타입이므로 배열도 참조타입이다.
둘의 큰 차이점은 원시타입은 값을 변화시킬 수 없는 불변의 값이고 참조타입은 변화가 가능한 값이다. 원시타입을 재할당을 하면 값이 바뀌는것 아닌가 라고 생각할 수 있는데, 재할당이라는 말을 다시 생각해보면 금방 이해가 될 수 있다.

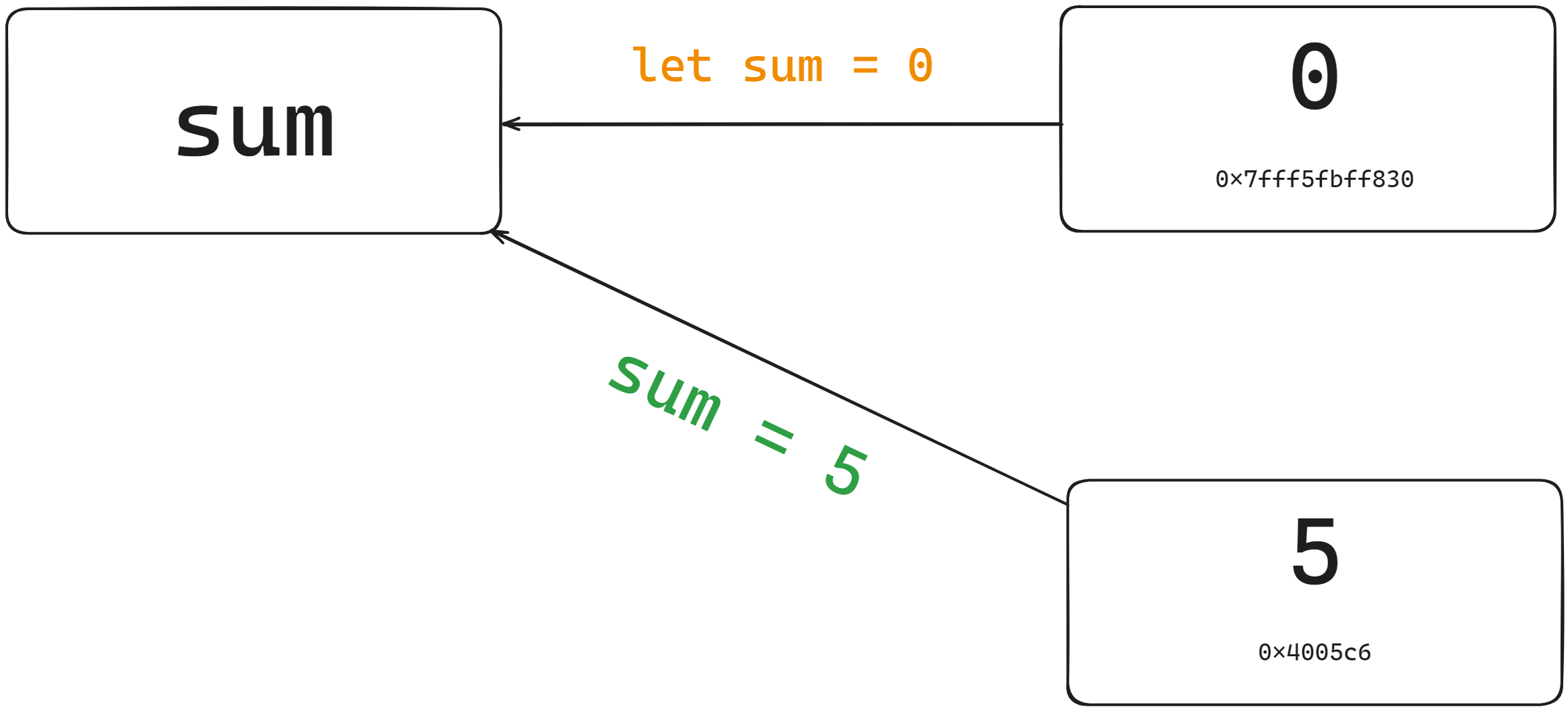
원시타입을 재할당하게 되면 해당 메모리주소의 값을 바꾸는게 아닌, 메모리 주소를 새로 옮기고 거기에 새로운 값을 재할당하는 것이다.

반대로 참조타입은 해당 메모리 주소를 참조하고 그 값을 바꿀 수 있다.

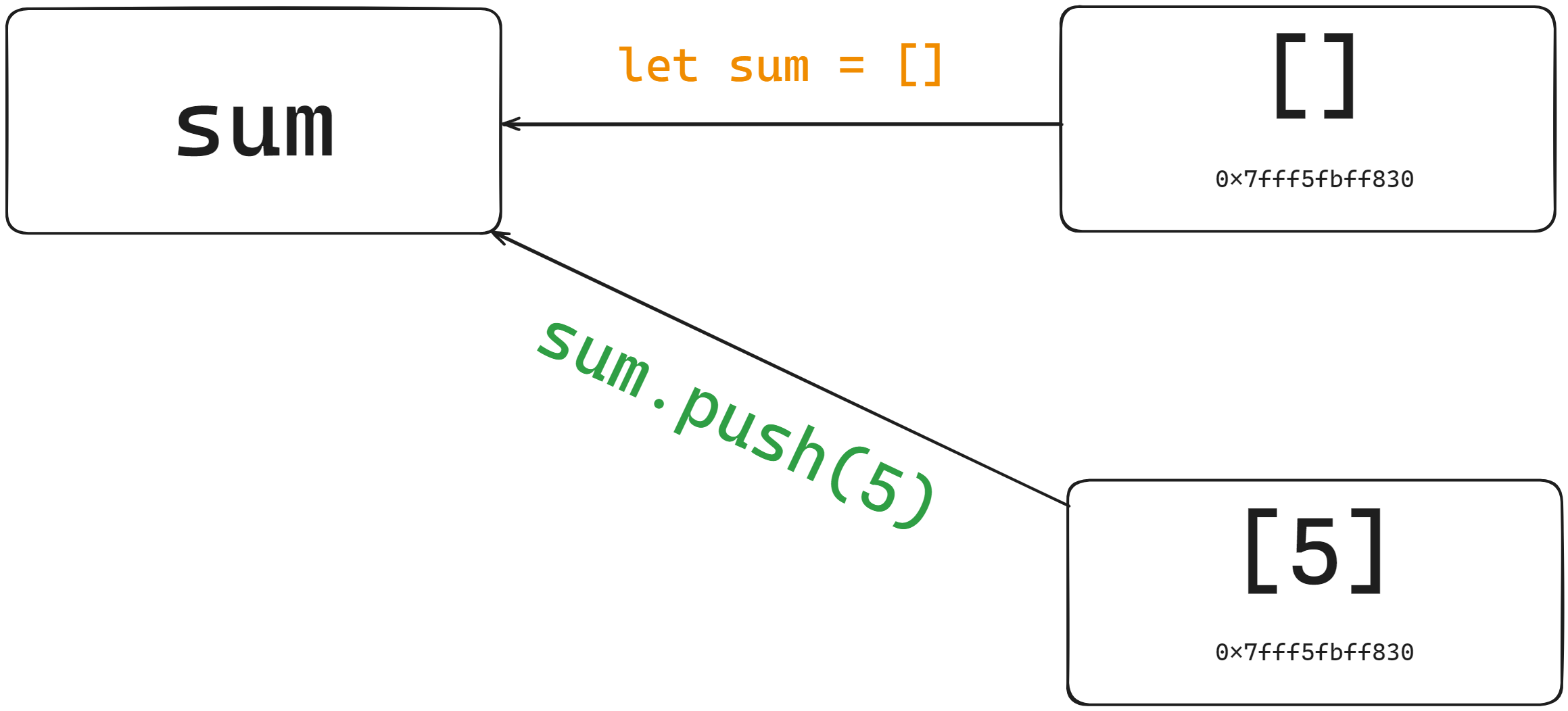
메모리 주소는 바뀌지 않고, 해당 값이 바뀌었다.

재할당이 유리한 이유

코드를 다시 살펴보면 나는 unshift()를 사용해서 배열의 맨 앞으로 8진수로 변환된 값을 넣어주려고 했다. 이것이 문제였다.
배열은 기존의 값을 가지고 연산을 하기 때문에 unshift()를 메서드를 수행하기 위해서 배열을 하나씩 밀고 맨 앞에 공간을 만든 뒤에 원소를 넣었다. 8진수가 길어지면 길어질수록 해당 수행과정은 늘어나기 때문에 O(N)의 시간복잡도가 나온다.
하지만, 문자열을 재할당하는것은 새로운 값을 만들기 때문에 O(1)의 시간복잡도를 나타낸다고 볼 수 있다.
만약 push()를 사용했다면 조금 달랐을까? 시간복잡도는 unshift()보다 개선될 수 있으나, 첫 문자열을 뒤집고 연산이 끝난뒤에 다시 뒤집은 다음 join()을 해줘야 하기 때문에 어찌되었든 재할당보다는 연산과정이 더 추가된다. 따라서 해당 문제에 한해서 재할당이 유리하다고 할 수 있다.

알고리즘 누가 안 중요하대?

비전공자들에게는 알고리즘은 너무나 높은 벽과 같고, 코테를 볼때마다 좌절하기 일쑤이다. 그래서 알고리즘이 실무에서는 필요없다는 스스로 위안을 삼고 그러한 근거의 글들을 찾아보며 공부안할 핑계를 찾는다. 내가 그랬다.
하지만, 하루에 하나씩 풀면서 느낀점은 이러한 기초들과 디테일들이 쌓여 프로젝트가 되고 서비스가 되는 것 같다.
회사에서 내 방식대로 코드를 짰을 때 연산을 너무 많이해서 서버비가 1억이 나오는 것을, 개선된 방법으로 하면 그 절반 혹은 그 이상의 값을 절약할 수도 있는 것이다. 만약, 내가 이러한 알고리즘을 풀지 않았더라면 몰랐을 노릇이다. 또한, 더 많은 문제를 풀면 이것보다 더 좋은 방법도 알 수 있을 것이다.
그러니까, 더 이상 핑계를 찾지말고 하루에 하나씩만 풀어보자. 별 것 아닌것 같은데 풀다보면 다음 패턴이 보이기 시작한다. 그렇게 하나씩 풀어보자. 한 번에 되는것은 없다.