문제

• 해당 그래프 0은 갈 수 있는 길 1은 벽이라 했을 때 2차원 리스트의 마지막 지점에 도착하는 최소 거리는 몇일까?
  
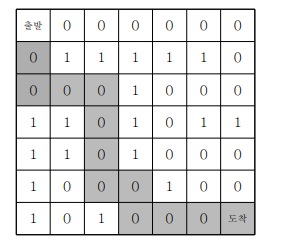
• 해당 그래프의 최단 거리는 12이다.

문제 풀이

from collections import deque

dx = [0,0,-1,1]
dy = [1,-1,0,0]
board = [list(map(int,input().split())) for _ in range(7)]
dist = [[0] * 7 for _ in range(7)]
q = deque()
q.append((0,0))
board[0][0] = 1

while q:
    now = q.popleft()
    for i in range(4):
        nx = now[0] + dx[i]
        ny = now[1] + dy[i]
        if 0<=nx<7 and 0<=ny<7 and board[nx][ny] == 0:
            dist[nx][ny] = dist[now[0]][now[1]] + 1
            board[nx][ny] = 1
            q.append((nx,ny))

if dist[6][6] == 0:
    print(-1)
else:
    print(dist[6][6])

• 전형적인 BFS로 최단거리 구하는 문제이다.
• 상하좌우로 움직여서 갈 수 있기 때문에 상하좌우를 확인한다.
• 이때 조건은 해당 리스트의 범위를 넘어가지 않아야 하고 이미 방문했던 곳이 아니어야 한다.
• 방문을 했다는 표시로 해당 리스트를 1로 만들어 다시 접근을 하지 못하게 해주었다.
• 해당 문제는 도착지점이 없이 마지막 지점을 도착지점으로 하기 때문에 중간에 종료 조건을 넣어주지 않았다.