[Algorithm] 플로이드-워셜 알고리즘
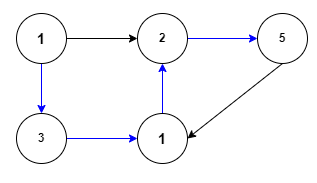
플로이드-워셜(floyd-warshall) 알고리즘
- 그래프에서 최단 거리를 구하는 알고리즘
- 음수 가중치 에지가 있어도 수행할 수 있음
- 동적 계획법의 원리를 이용해 알고리즘에 접근
시간 복잡도는 O(V^3)으로 매우 큰 편으로, 보통 이 알고리즘 문제가 나올 때는 N의 개수가 100이나 200으로 작은 편이다.
그래서 보통 N의 크기가 작은 문제일 때는 다른 알고리즘을 사용하지 않고 플로이드-워셜 알고리즘을 활용하면 된다고 판단하면 되는 경우가 많다.
플로이드-워셜 알고리즘의 가장 핵심적인 원리
A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때,
최단 경로 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단 경로라는 것
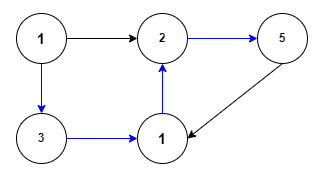
색칠한 에지 경로 1 -> 5가 최단 경로라면, 1 -> 4 최단 경로와 4 -> 5 최단 경로 역시 색칠된 에지로 이뤄질 수 밖에 없다.
도출한 플로이드-워셜 점화식
D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])
위의 점화식을 활용하면 플로이드-워셜 알고리즘을 이용하여 문제를 풀 수 있다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int M = Integer.parseInt(br.readLine());
int[][] distance = new int[N + 1][N + 1];
//인접 행렬 초기화
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (i == j) {
distance[i][j] = 0;
} else {
distance[i][j] = 10000001; //충분히 큰 수로 저장
}
}
}
//버스 비용 정보 저장
for (int i = 0; i < M; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
// 시작 도시와 도착 도시를 연결하는 노선은 여러 개일 수 있으므로, 그 중 최솟값을 저장함
if (v < distance[s][e]) {
distance[s][e] = v;
}
}
//플로이드-워셜 알고리즘 수행
for (int k = 1; k <= N; k++) { //거쳐가는 지점
for (int i = 1; i <= N; i++) { //시작 지점
for (int j = 1; j <= N; j++) { //도착 지점
if (distance[i][k] + distance[k][j] < distance[i][j]) {
distance[i][j] = distance[i][k] + distance[k][j];
}
}
}
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (distance[i][j] == 10000001) {
System.out.print("0 ");
} else {
System.out.print(distance[i][j] + " ");
}
}
System.out.println();
}
}
}이 외에도 플로이드-워셜 알고리즘을 변형하여 풀 수 있는 문제들이 있다.