벡터가 뭔가요?
-
벡터 : 숫자를 원소로 가지는 리스트 또는 배열
- 공간에서의 한 점을 나타냄
- 원점([0, 0]) 으로부터 상대적 위치를 표현
x = np.array([1, 7, 2]): 보통 행 벡터로 표현
-
1차원 공간 : x
-
2차원 공간 : [x, y]
-
3차원 공간 : [x, y, z]
-
n차원 공간 : n개의 축을 가지는 좌표평면에서의 한 점
-
벡터에 숫자를 곱해주면 길이만 변한다.
αx = [αx1, αx2, ... αx5]
→ αx를 스칼라곱이라고 부름
-
α > 1 : 1보다 크면 길이가 늘어남
-
0 < α < 1 : 1보다 작으면 길이가 줄어듬
-
α < 0 : 단 0보다 작으면, 반대 방향이 됨
벡터끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있다.
x = [x1, x2, ... xd]
y = [y1, y2, ... yd]
x ± y = [x1 ± y1, x2 ± y2, ... xd ± yd]
일반적으로 다른 모양의 벡터끼리 덧셈, 뺄셈을 하게 되면, numpy에서 오류가 나게 된다.
벡터끼리 같은 모양을 가지면 성분곱(Hadamard product)을 계산할 수 있다.
x = [x1, x2, ... xd]
y = [y1, y2, ... yd]
x ⊙ y = [x1y1, x2y2, ... xdyd]
┌──(numpy-env)─(kali㉿kali)-[~]
└─$ python3
Python 3.13.2 (main, Feb 5 2025, 01:23:35) [GCC 14.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import numpy as np
>>> x = np.array([1, 7, 2])
>>> y = np.array([5, 2, 1])
>>> x + y
array([6, 9, 3])
>>> x - y
array([-4, 5, 1])
>>> x * y
array([ 5, 14, 2])벡터의 덧셈
두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현함
- 원점은 주로 '제로벡터', '원벡터' 라고도 함
x = 0 + x
제로벡터의 자리에 다른 숫자를 넣게 된다면, x는 그 숫자만큼 위치가 이동하는 것을 의미한다.
벡터의 뺄셈
두 벡터의 뺄셈은 다른 벡터로부터 상대적 위치이동을 표현함
원래 x 벡터 방향의 반대 방향으로 이동하는 것임
- 뺄셈은 방향을 뒤집은 덧셈
벡터의 노름
벡터의 노름(norm) : 원점에서부터의 거리
- 원점에서부터 한 점 사이의 거리를 의미함
x = [x₁, x₂, ..., x_d]
‖x‖₁ = Σ₍ᵢ₌₁₎⁽ᵈ⁾ |xᵢ|
‖x‖₂ = √(Σ₍ᵢ₌₁₎⁽ᵈ⁾ |xᵢ|²)
노름이라는 기호는 n차원에 대해 성립하는 것이 아니라, 임의의 차원 d에 대해 성립하는 것이다.
- L1-노름 : 각 성분의 변화량의 절대값을 모두 더해주는 것
- x, y 좌표축을 따라 이동하는 거리를 더해주는 것
- L2-노름 : 피타고라스 정리를 이용해 유클리드 거리를 계산하는 것
- x, y 좌표축을 따라 이동한 좌표값에 절대값을 씌워준 후, 제곱이 된 성분곱을 더해준 후 제곱근 연산을 진행하게 됨
노름의 종류에 따라 기하학적 성질이 달라진다.
- L1-노름 상의 원 :
x: ‖x‖₁ = 1- 예: Robust 학습, Lasso 회귀
- L2-노름 상의 원 :
x: ‖x‖₂ = 1- 예 : Laplace 근사, Ridge 회귀
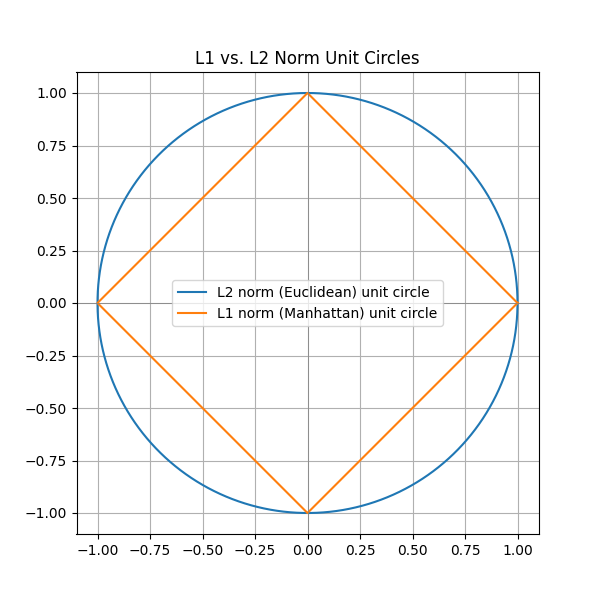
기계학습에 사용되는 목적에 따라 노름의 종류를 다르게 사용한다.
벡터 사이의 거리 구하기
L1, L2-노름을 이용하여 두 벡터 사이의 거리를 계산할 수 있다.
즉, 두 점이 주어졌을 때 두 점 사이의 거리를 구하는 것이다.
두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용한다.
y - x벡터란:-x: x 벡터를 반대 방향으로 이동한 다음y: 0에서 y벡터로 이동한 후,y-x: 그 이동한 위치인 y 벡터에서-x만큼 이동한 거리
상대적 위치를 이용한 것
- ‖y - x‖ = ‖x - y‖
벡터 사이의 각도 구하기
L2-노름인‖·‖₂만 각도 계산이 가능하다.
피타고라스 정리에 의해서 유클리드 거리를 계산할 수 있게 되는데,
0벡터, x벡터, y벡터를 이용, 제2 코사인 법칙에 의해 두 벡터 사이의 각도를 계산할 수 있다.
분자를 쉽게 계산하는 방법이 내적이다.
cos(θ) = (x · y) / (|x| * |y|)(x · y): 두 벡터의 내적|x|: 벡터 a의 크기(노름)|y|: 벡터 b의 크기(노름)
내적은 np.inner을 이용해서 계산한다.
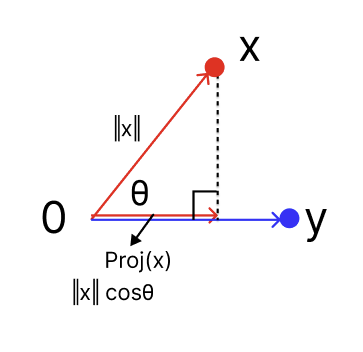
내적은 정사영(orthogonal projection)된 벡터의 길이와 관련 있다.
- Proj(x) 는 벡터 y로 정사영된 벡터 x의 그림자를 의미한다.
- 두 벡터의 유사도를 측정하는데 사용 가능하다.
즉 내적은 정사영의 길이를 벡터 y의 길이 ‖y‖만큼 조정한 값이다.
<x, y> = ‖x‖₂‖y‖₂cos(θ)
Reference
