Logistic Regression Classifier

연·2025년 8월 2일

just공부

목록 보기
37/41

Overview

Classification Problem

Linear Regression으로 학습해보자

f(x)=−2.4507508832597606+0.00227488∗RPM+0.00379006∗Vibrationf(x) = -2.4507508832597606 + 0.00227488 * RPM + 0.00379006 * Vibration

기존 접근의 문제점들

  • 1 이상 또는 0 이하의 수들이 나오는 걸 어떻게 해석해야 하는가?
  • 1 또는 0으로 정확히 표현 가능한가?
    • Status={1if f(x)≥00otherwise\text{Status} = \begin{cases} 1 & \text{if } f(x) \geq 0 \\ 0 & \text{otherwise} \end{cases}
  • 변수가 Y에 영향을 주는 정도가 비례하는가?
  • 확률로 발생할 사건의 가능성을 표현해야 한다.

Solution

→ 확률로 나타내자

logit(x)=11+e−x\text{logit}(x) = \frac{1}{1 + e^{-x}}

Sigmoid function

어떤 사건이 일어날 확률

P(X)일어날확률P(X)\\ 일어날 확률
1−P(X)일어나지않을확률1 - P(X) \\ 일어나지 않을 확률
0≤P(X)≤10 ≤ P(X) ≤1
  • 어떤 사건이 일어날 확률과 일어나지 않은 확률의 비율을 가지고 구하게 되는 것이다.

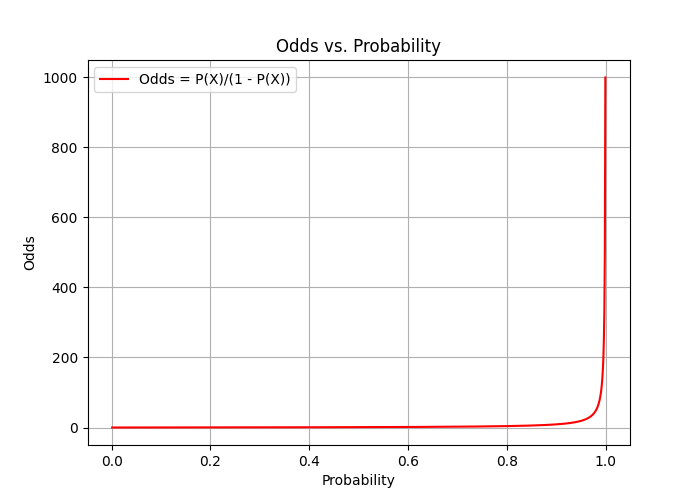
Odds Ratio

해당 사건이 일어날 확률과 일어나지 않을 확률

일어날 확률P(X)일어나지 않을 확률1−P(X)\frac{\text{일어날 확률} P(X)}{\text{일어나지 않을 확률} 1 - P(X)}

  • 위의 그래프에서는 xx 값 자체가 확률이다

Logit function

X의 값이 주어졌을 때 y의 확률을 이용한 log odds

logit(p(y=1∣x))=log⁡e(p1−p)=log⁡e(p)−log⁡e(1−p)=−log⁡e(1p−1)\text{logit}\left(p(y = 1 \mid x)\right) = \log_e\left( \frac{p}{1 - p} \right) \\ = \log_e(p) - \log_e(1 - p) \\ = -\log_e\left( \frac{1}{p} - 1 \right) \\
  • 역함수로 치환되고, -가 앞에 오게 된다.

Sigmoid(=Logistic) Function

  • Logit 함수의 역함수로 z에 관한 확률을 산출해주는 것이다.
    f(z)=y=−log⁡e(1z−1)z=−log⁡e(1y−1)f(z) = y = -\log_e\left( \frac{1}{z} - 1 \right) \\ z = -\log_e\left( \frac{1}{y} - 1 \right)
  • 로지스틱 함수의 역함수로, logit 변환과 역변환 관계를 설명한다.
  • 역함수로 바꾸면 y에 관한 정리가 된다.
z=−log⁡e(1y−1)z = -\log_e\left( \frac{1}{y} - 1 \right)
e−z=1−yye^{-z} = \frac{1 - y}{y} \\
y⋅e−z+y=1y \cdot e^{-z} + y = 1 \\
y(e−z+1)=1y(e^{-z} + 1) = 1 \\
y=11+e−zy = \frac{1}{1 + e^{-z}} \\
  • logit 함수의 역함수가 sigmoid 함수임을 증명하는 과정이다.

- Logistic Function = Inverse of logit function

  • 미분 가능한 연속구간으로 변환
  • S형태로 닮았다고 하여 sigmoid function이라고 칭한다.
p=σ(z)=11+e−z,p1−p=11+e−ze−z1+e−z=1e−z=ezlog⁡e(p1−p)=zlog⁡e(p1−p)=z=w0x0+w1x1+⋯+wnxnp = \sigma(z) = \frac{1}{1 + e^{-z}}, \quad \frac{p}{1 - p} = \frac{\frac{1}{1 + e^{-z}}}{\frac{e^{-z}}{1 + e^{-z}}} = \frac{1}{e^{-z}} = e^z \\ \log_e \left( \frac{p}{1 - p} \right) = z \\ \log_e \left( \frac{p}{1 - p} \right) = z = w_0 x_0 + w_1 x_1 + \cdots + w_n x_n

Cost function

가설함수

hθ(x)=g(z)=11+e−zwhere:z=w0x0+w1x1+⋯+wnxn=θTxh_{\theta}(x) = g(z) = \frac{1}{1 + e^{-z}} \\ where: z = w_0 x_0 + w_1 x_1 + \cdots + w_n x_n \\ = \theta^T \mathbf{x}
0≤hθ(x)≤10 \leq h_{\theta}(x) \leq 1

위의 수식에서 우리가 구하고자 하는 것은 zz값이다.
zz값은 ww와 xx의 linear combination으로 이루어져 있다.
zz값에 따른 확률값 hθ(x)h_{\theta}(x)을 구할 수 있다.

Cost function

Cost Function을 구하는 방법은 크게 두가지가 있다.
MLE라는 방식으로 구하는 것이고, 다른 하나는 그래프를 그려 보면 알 수 있다.

Cost(hθ(x),y)={−log⁡(hθ(x))if y=1−log⁡(1−hθ(x))if y=0\text{Cost}(h_\theta(x), y) = \begin{cases} -\log(h_\theta(x)) & \text{if } y = 1 \\ -\log(1 - h_\theta(x)) & \text{if } y = 0 \end{cases}

1. MLE(Maximum Likelihood Estimation) 로 비용 함수 유도
로지스틱 회귀는 각 데이터에 대해 확률을 예측한다.
모델 파라미터 θ\theta가 주어졌을 때, 전체 데이터가 관측될 확률을 최대화하고자 한다.
이 확률을 likelihood라고 부르고, 이를 최대화하는 것이 MLE이다.

2. 비용함수 그래프의 형태
Cost 함수는 아래와 같은 특징을 가진다.

  • y=1y = 1일 때, hθ(x)h_{\theta}(x)가 1에 가까울 수록 비용 ↓
  • y=0y = 0일 때, hθ(x)h_{\theta}(x)가 0에 가까울 수록 비용 ↓
  • 예측이 틀릴수록 비용이 급격히 증가한다.

ex.

  • y=1:−log⁡(hθ(x))→0y = 1: - \log(h_{\theta}(x)) → 0에 가까워지면 비용 급상승
  • y=0:−log⁡(1−hθ(x))→1y = 0: - \log(1 - h_{\theta}(x)) → 1에 가까워지면 비용 급상승

비용함수 평균 J(θ)J(\theta)

J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \text{Cost}\left(h_\theta(x^{(i)}), y^{(i)}\right)
  • J(θ)J(\theta): 전체 데이터셋에 대한 평균 비용 (로스 함수)
  • mm: 전체 데이터 수
  • Cost(hθ(x(i)),y(i))Cost\left(h_\theta(x^{(i)}), y^{(i)}\right) : 앞서 본 이진 분류용 비용 함수
=−1m∑i=1m[y(i)log⁡hθ(x(i))+(1−y(i))log⁡(1−hθ(x(i)))]= -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log h_\theta(x^{(i)}) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]
  • Cross-Entropy 형태로 전개
    • 개별 비용 함수를 전개한 형태이다.
    • y(i)=1y^{(i)} = 1일 때: 첫 항만 살아남아 −log⁡hθ(x(i))-\log h_\theta(x^{(i)})
    • y(i)=0y^{(i)} = 0일 때: 두 번째 항만 살아남아 −log⁡(1−hθ(x(i)))- \log(1 - h_{\theta}(x^{(i)}))
  • 위의 두 경우를 모두 커버할 수 있는 하나의 식으로 만든 것이다.
find θ, where min⁡θJ(θ)\text{find } \theta \text{, where } \min_{\theta} J(\theta)
  • 이 비용 함수 J(θ)J(\theta)를 최소화하는 최적의 파라미터 θ\theta를 찾는 것이 목표이다.
  • 이를 위해 경사하강법(Gradient Descent) 등을 사용한다.

시그모이드 함수 hθ(x)h_{\theta}(x)

hθ(x)=11+e−θTxh_\theta(x) = \frac{1}{1 + e^{-\theta^T \mathbf{x}}}
  • 로지스틱 회귀의 가설 함수(Hypothesis Function)이며, 입력값에 대해 확률 출력을 반환한다.
  • 출력값은 항상 0~1 사이이다.

Partial derivation of cost function

J(θ)=−1m∑i=1m[−y(i)log⁡(1+e−θx(i))+(1−y(i))(−θx(i)−log⁡(1+e−θx(i)))]J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ -y^{(i)} \log(1 + e^{-\theta x^{(i)}}) + (1 - y^{(i)})( -\theta x^{(i)} - \log(1 + e^{-\theta x^{(i)}}) ) \right]
  • 로지스틱 회귀의 비용 함수에서 시작하여 각 항을 시그모이드 정의로 치환했다.
  • hθ(x)=11+e−θTxh_\theta(x) = \frac{1}{1 + e^{-\theta^T \mathbf{x}}} 이 식을 비용 함수에 대입하면 로그 함수와 지수 함수가 결합된 형태가 된다.
J(θ)=−1m∑i=1m[yiθxi−log⁡(1+e−θxi)]=−1m∑i=1m[yiθxi−log⁡(1+eθxi)]J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y_i \theta x^i - \log(1 + e^{-\theta x^i}) \right] \\ = -\frac{1}{m} \sum_{i=1}^{m} \left[ y_i \theta x^i - \log(1 + e^{\theta x^i}) \right]
  • 정리를 하면 위와 같은 수식이 나오게 된다.
−θxi−log⁡(1+e−θxi)=−[log⁡(eθxi)+log⁡(1+e−θxi)]=−log⁡(1+eθxi)-\theta x^i - \log(1 + e^{-\theta x^i}) = -\left[ \log(e^{\theta x^i}) + \log(1 + e^{-\theta x^i}) \right] \\ = -\log(1 + e^{\theta x^i})
  • 복잡한 로그 표현을 단일 로그로 변환하여 계산을 간단하게 해줄 수 있다.

Partial derivation of cost function

로지스틱 회귀의 비용 함수 J(θ)J(\theta)를 파라미터 θj\theta_j에 대해 편미분 하는 과정이다.

−1m∑i=1m[yiθxi−log⁡(1+eθxi)]-\frac{1}{m} \sum_{i=1}^{m} \left[ y_i \theta x^i - \log(1 + e^{\theta x^i}) \right]

여기서 z=θTxz = \theta^T x 이며, θxi=∑j=1nθjxji\theta x^i = \sum_{j=1}^{n} \theta_j x_j^i

θ에 관하여 편미분하면:\textbf{θ에 관하여 편미분하면:}

∂∂θj(yiθxi)=yixji\frac{\partial}{\partial \theta_j} \left( y_i \theta x^i \right) = y_i x_j^i

기초 미분 성질 예시

ddxln⁡(2x)=22x=1x,ddxe2x=2e2x\frac{d}{dx} \ln(2x) = \frac{2}{2x} = \frac{1}{x}, \qquad \frac{d}{dx} e^{2x} = 2e^{2x}

로그 항 미분

∂∂θjlog⁡(1+eθxi)=xjieθxi1+eθxi=xji⋅hθ(xi)\frac{\partial}{\partial \theta_j} \log(1 + e^{\theta x^i}) = \frac{x_j^i e^{\theta x^i}}{1 + e^{\theta x^i}} = x_j^i \cdot h_\theta(x^i)

로지스틱 회귀의 비용 함수 미분 중 유도 과정

∂∂θjlog⁡(1+eθxi)=xjieθxi1+eθxi=xjihθ(xi),\frac{\partial}{\partial \theta_j} \log(1 + e^{\theta x^i}) = \frac{x_j^i e^{\theta x^i}}{1 + e^{\theta x^i}} = x_j^i h_\theta(x^i),
여기서 hθ(xi)=11+e−θxi\quad \text{여기서 } h_\theta(x^i) = \frac{1}{1 + e^{-\theta x^i}}
xjieθxi1+eθxi=xjie−θxi∗11+eθxi=xjie−θxi+1=xji1+e−θxi=xji⋅hθ(xi)\frac{x_j^i e^{\theta x^i}}{1 + e^{\theta x^i}} = \frac{x_j^i}{e^{-\theta x^i}} * \frac{1}{1 + e^{\theta x^i}} \\ = \frac{x_j^i}{e^{-\theta x^i} + 1} = \frac{x_j^i}{1 + e^{-\theta x^i}} \\ = x_j^i \cdot h_\theta(x^i)
where hθ(xi)=11+e−θxi\quad \text{where } h_\theta(x^i) = \frac{1}{1 + e^{-\theta x^i}}
profile
연
Whatever I want | Interested in DFIR, Security, Infra, Cloud
이전 포스트

Linear Regression - Polynomial Regression

다음 포스트

딥러닝 연구의 패러다임

0개의 댓글