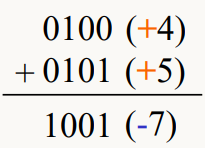1.1 논리 설계

디지털 시스템(Digital systems) : 임의 개수의 입력과 임의 개수의 출력이 있는 시스템. 데이터 입력 외에 클럭이라 불리는 타이밍 신호가 있는 경우도 있다.

디지털 시스템의 종류

1. 조합 시스템(Combinational Logic System) : 시스템 state 가 필요 없다.
   → Output = Function(Input)
2. 순차 시스템(Sequential System) : 시스템 state가 필요한 시스템, 기억 장치(메모리)가 있는 시스템
   a) Synchronous Sequential System : state가 이산적으로 업데이트 되는 시스템.
   b) Asynchronous Sequential System : state가 연속적으로 업데이트 되는 시스템.
   → State = Function(State, Input)
   → Output = Function(State) || Function(State, Input)

디지털 시스템의 예시

1. Digital Counter
   
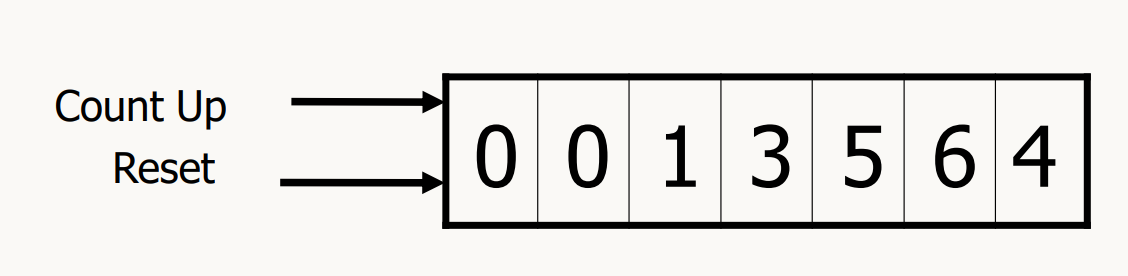
   Input : Count Up, Reset
   Output : Visual Display
   State : "Value" of stored digits
   → Asynchronous Sequential System (클락이 없기 때문에)

2. Digital Computer
   
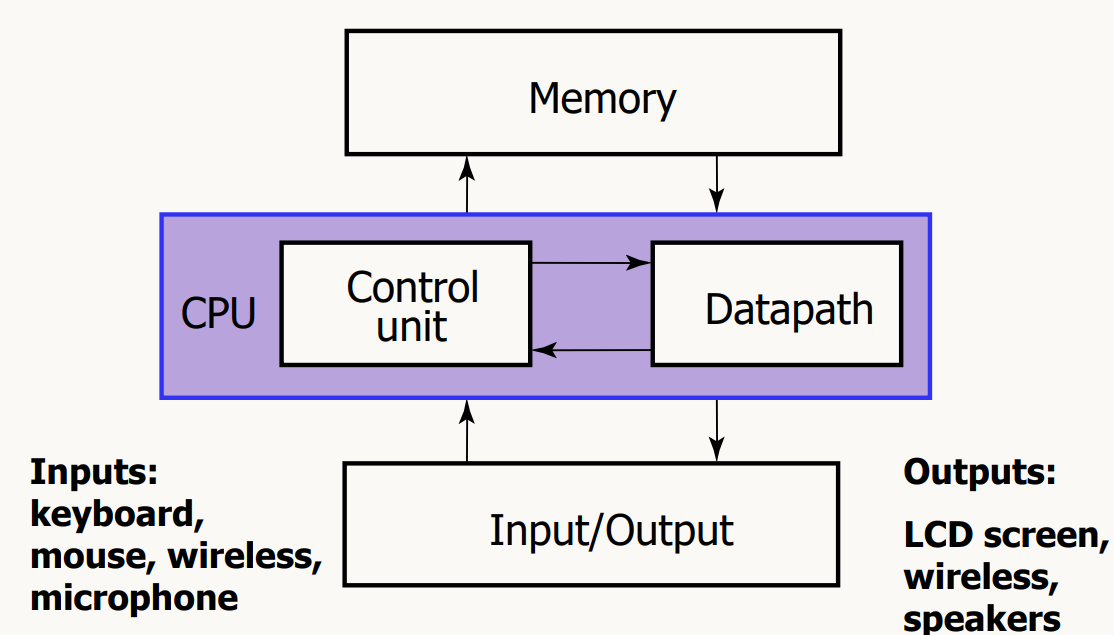
   → Synchronous Sequential System (CPU라는 클락이 있기 때문에)

3. Embedded Systems
   내장형 컴퓨터. 자동차, 스피커, 스마트폰, PC, TV 등등

---

1.2 진법에 대한 복습

1.2.1 Binary Value

디지털 시스템에선 정보를 전달하는 방법을 Binary Value 사용
연속적인 값 → 0 or 1

0	1
False	True
Low	High
Off	On

• Digital : 이산적인 값, 정수 값을 가짐
• Analog : 실수 값을 가짐, continuous in value & time
  
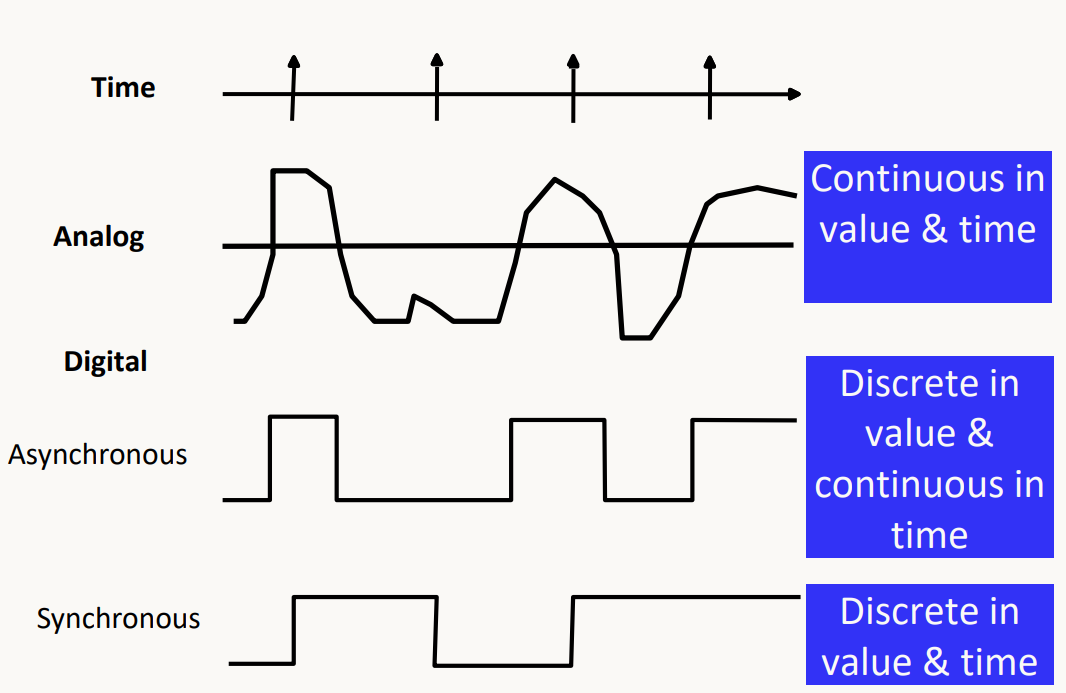
  Time : 주기적으로 발생하는 event, clock
  Asynchronous : clock과 비동기화, 시간 연속적, 값 불연속적
  Synchronous : clock과 동기화, 시간&값에서 불연속적

1.2.2 Number System

n : number of digits
r : radix or base(밑)
ai : coefficients(계수) (0 ≤ ai < r)

ex)
$7642_{10}=7×10^3+6×10^2+4×10^1+2$
$101111_2=1×2^5+0×2^4+1×2^3+1×2^2+1×2^1+1\\\quad \quad \quad \,\,\,\, = 32+8+4+2+1=47_{10}$

10진수 : Demical number
2진수 : Binary number
8진수 : Octal number (3개씩 끊기)
16진수 : Hexademical number (0~9, A~F / 4개씩 끊기)

1.2.3 정수의 음수 / 양수 표현법

Signed-Magnitude Representation : 부호-값 표현

→ 잘 사용되지 않는다

MSB : Most Significant Bit, 가장 중요한 비트, 부호를 표현

MSB 부호를 사용해 표현.
Range : 0을 기준으로 대칭

$-(2^{n-1}-1)$ ~ $(2^{n-1}-1)$

→ 0 표현 방법이 2개 : +0, -0

2' Complement : 2의 보수 방법

→ 주로 이 방법을 사용한다
1. 음수일 때, 2진수로 변환
2. 보수를 취함 (0 → 1 / 1 → 0)
3. 1을 더함 (비트 한계를 넘어가는 값은 무시)

Range : 음수가 1개 더 많음. 0이 1개이다.

$-(2^{n-1})$ ~ $(2^{n-1}-1)$

Binary	Positive	Signed
0000	0	0
0001	1	+1
0010	2	+2
0011	3	+3
0100	4	+4
0101	5	+5
0110	6	+6
0111	7	+7
1000	8	-8
1001	9	-7
1010	10	-6
1011	11	-5
1100	12	-4
1101	13	-3
1110	14	-2
1111	15	-1

1.2.4 이진수의 덧셈과 뺄셈

- 덧셈

각 자리 끼리 더함. 다음 비트에 대한 캐리까지 더한다.

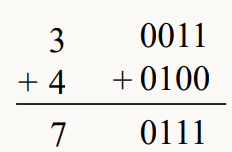
오버플로우(Overflow) : 산술 연산의 결과가 정해진 범위를 벗어날 때

덧셈에서 서로 같은 부호를 더했는데 반대 부호가 나올 떄.

- 뺄셈

두 번째 피연산자에 대해 2의 보수를 취하고 두 수를 더하는 방식을 사용한다.
a-b는 a + (-b) 와 같이 계산된다.

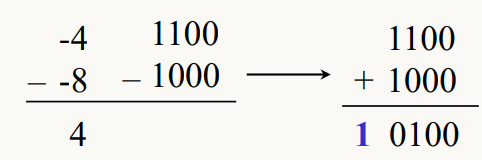
연산 과정중 오버플로우는 괜찮다.

---

1.3 BCD 코드

BCD(Binary Coded Decimal) : 이진코드 십진수

10진수를 표현하는 여러가지 방법들

Decimal digit	8421 code	5421 code	2421 code	Excess 3 code	8,4,-2,-1 code
0	0000	0000	0000	0011	0000
1	0001	0001	0001	0100	0111
2	0010	0010	0010	0101	0110
3	0011	0011	0011	0110	0101
4	0100	0100	0100	0111	0100
5	0101	1000	1011	1000	1011
6	0110	1001	1100	1001	1010
7	0111	1010	1101	1010	1001
8	1000	1011	1110	1011	1000
9	1001	1100	1111	1100	1111

1. 8421 code : 일반적인 이진법 코드
2. 5421 code : 첫 번째 비트가 5를 의미
3. 2421 code : 첫 번째 비트가 2를 의미
4. Excess 3 code : 3를 더한 값을 표시 (0~4, 5~9 보수 관계)
5. 2 of 5 code : 5개 비트 중 2개만 사용 → 에러 찾기 용이
6. 8,4,-2,-1 code : 각 비트가 8,4,-2,-1을 의미 (0~4, 5~9 보수 관계)

BCD 코드에서 덧셈의 오류 → 6을 더한다

• 용어 정리

  binary number ↔ decimal number : conversion
  decimal number ↔ BINARY CODE : coding

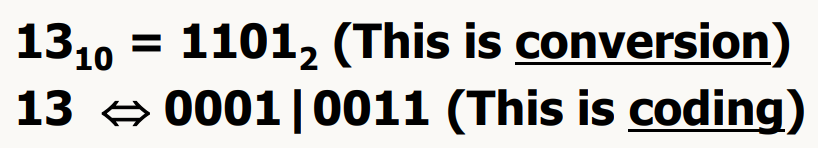
1.4 기타 코드들

1. Gray Code

• 일종의 채널 코딩. 숫자간 한 비트씩 차이남

Number	Gray code	Number	Gray code
0	0000	8	1100
1	0001	9	1101
2	0011	10	1111
3	0010	11	1110
4	0110	12	1010
5	0111	13	1011
6	0101	14	1001
7	0100	15	1000

2. Hamming Code

• Hamming 이 제작한 코드
• Single error correction code : error를 찾고 수정까지 할 수 있음
• 4개의 data bits, 3개의 check bits(a1, a2, a4)

Check bits
a1 = a3 ⊕ a5 ⊕ a7
a2 = a3 ⊕ a6 ⊕ a7
a4 = a5 ⊕ a6 ⊕ a7

Error Detecting bits
e1 = a1 ⊕ a3 ⊕ a5 ⊕ a7
e2 = a2 ⊕ a3 ⊕ a6 ⊕ a7
e4 = a4 ⊕ a5 ⊕ a6 ⊕ a7

e는 모두 0이 나와야 한다. (자기 자신과 자기 자신의 XOR이기 때문)
→ 1이 나오면 오류

오류인 bit : 4e4 + 2e2 + e1

n의 check bit가 있다면, 2n-n-1개의 information bit가 있을 수 있다.