Module #1: Foundation of Logic

서론

이산구조란 무엇인가? 사실은 이산수학에 대한 내용이 대부분이다.
Discrete 한 value들에 대한 연산, 구조, 내용들을 다룬다.

1. Basic Definition

명제(Proposition) : 참 또는 거짓 중 하나를 나타내는, 선언적 문장

의문문, 명령문, 감탄문 등은 참/거짓 판정이 불가하기에 명제가 아니다.
x + 1 = 2 와 같은 명제는 값이 배정되지 않은 변수(x)가 존재하므로 명제가 아니다.

연산자(Operator) : 한 개 이상의 명제를 조합해주는 것

단일연산자(Unary) : 1개의 명제를 가짐
이항연산자(Binary) : 2개의 명제를 연결함(접속사)

논리 연산자

부정 : p가 명제가 하면 p의 부정(negation)은 ~p로 표기된다.

논리곱 : p, q가 명제면 p와 q의 논리곱(conjunction)은 p ∧ q로 표기된다. 이는 'p and q'를 의미한다.

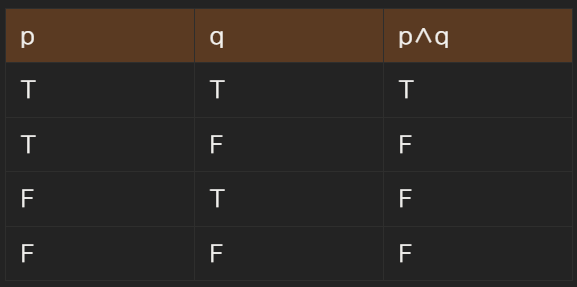
논리합 : p, q가 명제면 논리합(disjuction)은 p ∨ q로 표기된다. 이는 'p or q'를 의미한다.

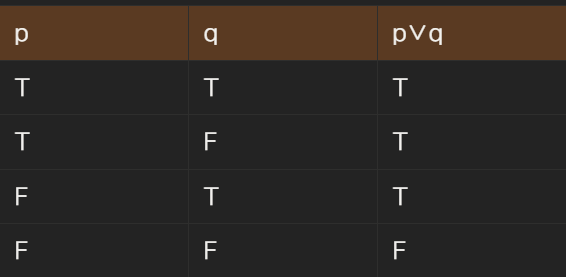
영어에서 or은 포괄적 논리합 / 베타적 논리합의 의미로 사용될 수 있다. 논리합 ∨은 포괄적 논리합에 대응한다.

여러 연산자가 같이 사용될 때

부정(~) 기호가 가장 높은 우선순위를 지닌다.
∧과 ∨이 동시에 사영될을 때는 ∧이 더 높은 우선순위를 지닌다.
그렇지만 괄호를 잘 사용해 헷갈릴 일이 없도록 하자.


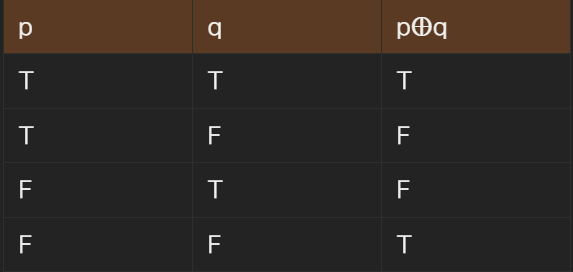
베타적 논리합 : 베타적 논리합 : p, q가 명제면 p와 q의 베타적 논리합(disjunction)은 p ⊕ q로 표기된다. 이는 ‘p exclusive-or q’를 의미한다.

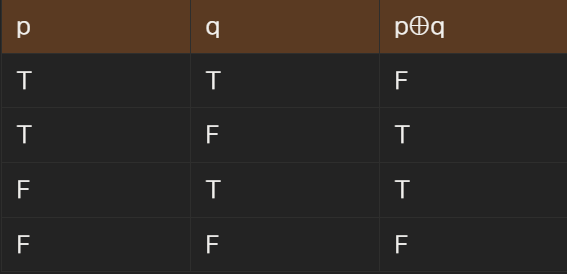
조건문(함축) : p, q가 명제면 p와 q의 조건문(implication)은 p → q로 표기된다. 이는 ‘if p, then q’를 의미한다. 이때 p를 가정, q를 결론이라고 한다.

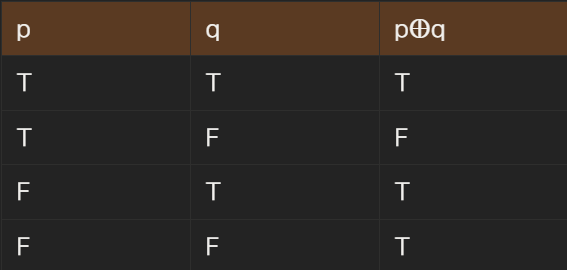
가정이 거짓이면 항상 참임을 유의하자.

• p→q 의 영어 표현들
  • if p, q / q if p / if p, then q
  • p only if q / q provided that p
  • p is sufficient for q / q is necessary for p
  • p implies q / q is implied by p
  • when p, q / q when p / whenever p, q

조건문 p → q에 대해
역(converse) : q → p
이(inverse) : ~p → ~q
대우(contrapositive) : ~q → ~p

조건문 p→q가 참이라면, 대우 ~q → ~p도 항상 참이다.

상호 조건문 : p, q가 명제면 p와 q의 상호 조건문(biconditional statement)은 p ↔ q로 표기된다. 이는 ‘p if and only if(iff) q’를 의미한다.

비트(bit)와 비트 연산자

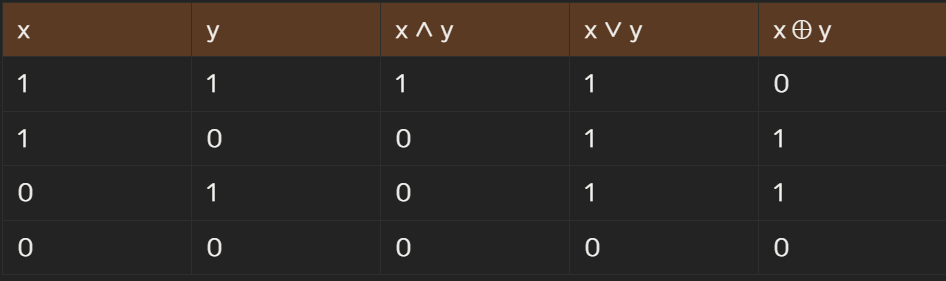
비트(bit) : binary digit. 0 또는 1로 구성된 이진수

• 0은 거짓, 1은 참을 의미한다.
• +은 'or'을 의미하고, · 은 'and'를 의미한다
  

비트 문자열 : 0개 이상의 비트를 갖는 비트열

---

2. Propositional Equivalence

동치(equivalent) : 두 개의 복합명제가 항상 같은 진리값을 가질 경우

항진명제(tautology) : 복합명제를 구성하고 있는 명제 변수가 어떠한 진리값을 갖는다 하여도 전체 복합 명제의 값이 항상 참일 때

모순(contradiction) : 복합명제를 구성하고 있는 명제 변수가 어떠한 진리값을 갖는다 하여도 전체 복합 명제의 값이 항상 거짓일 때

Equivalence Laws 동치 규칙들

항등 법칙 Identity : p ∧ T ≡ p / p ∨ F ≡ p

지배 법칙 Domination : p ∨ T ≡ T / p ∧ F ≡ F

등멱 법칙 Idempotent : p ∧ p ≡ p / p ∨ p ≡ p

이중 부정 법칙 Double negation : ~(~p) ≡ p

교환 법칙 Commutative : p ∨ q ≡ q ∨ p / p ∧ q ≡ q ∧ p

결합 법칙 Associative : p ∨ (q ∨ r) ≡ (p ∨ q) ∨ r / p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r

분배 법칙 Distributive : p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) / p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)

드 모르간의 법칙 : ~(p∧q) ≡ ~p ∨ ~q / ~(p∨q) ≡ ~p ∧ ~q

부정 법칙 : p ∨ ~p ≡ T / p ∧ ~p ≡ F

흡수 법칙 : p ∨ (p ∧ q) ≡ p / p ∧ (p ∨ q) ≡ p

T는 항진 명제, F는 모순 명제

동치로 논리 연산자 정의하기

베타적 논리합 : p⊕q ≡ (p ∨ q) ∧ ~(p ∧ q)

조건문 : p → q ≡ ~p ∨ q / p → q ≡ p ∧ ~q

상호 조건문 : p ↔ q ≡ (p→q) ∧ (q→p)