[자료구조] 01. Basic Comcepts

1. System Life cycle

• Requirement : 요구사항. 주어진 자료 입력 + 생성해내야 하는 결과(출력)
• Analysis : 분석.
  • bottom-up : 밑에서 위로. 코딩에 주안점을 둠
  • top-down : 문제를 분석해 작은 단위로 분리해 해결 → 더 좋은 방식
• Design : 설계. 추상 데이터 타입(ADT) + 알고리즘 설계
• Refinement and Coding : 자료 객체에 대한 표현 선택 & 알고리즘 작성
• Verification : 검증. 프로그램 정확성 체크, 테스트 & 오류 수정
  • 시간 복잡도 : running time
  • 공간 복잡도 : amount of memory used

---

2. Algorithm Specification

2.1 알고리즘이란?

• 알고리즘 : 특정한 일을 수행하는 명령어들의 유한 집합
  1) Input : 입력. 외부에서 제공되는 데이터가 0개 이상 존재
  2) Output : 출력. 적어도 한 개 이상의 결과를 생성
  3) Definiteness : 각 단계들은 명확해야 함.
  4) Finiteness : 알고리즘은 유한시간 안에는 반드시 끝나야 함.
  5) Effectiveness : 모든 명령은 종이와 연필만으로 수행할 수 있을 정도로 기본적이어야 함.

• 알고리즘 표현 : 자연어, flowchart, 프로그래밍 언어

Selection Sort
1st : finding the smallest integer;
2nd : exchange (함수 or macro);

for (i=0; i<n; i++){
    Examine list[i] to list[n-1]
    and suppose that the smallest integer is at list[min]
    Interchange list[i] and list[min]
}

// Swap Function
void swap(int *x, int *y){
	int temp = *x;
    *x = *y;
    *y = temp;
}

// Call : swap(&a, &b)

// Swap Macro
#define SWAP(x,y,t) ((t) = (x), (x) = (y), (y) = (t)

// Selection Sort 
void sort(int list[], int n){
  	int i, j, min, temp;
  	for(i = 0; i < n-1; i++){
    	min = i;
    	for(j = i+1; j < n; j++)
      	if(list[j] < list[min]) 
        	min = j;
   		SWAP(list[i], list[min], temp);
  	}
}

• Sort 알고리즘은 n $\geq$ 1 이상의 정수들의 모음을 정렬한다.

Binary Search
1st : 아직 검사할 정수가 남아 있는지 결정
2nd : searchnum과 list[middle] 비고

while(there are more integers to check){
    middle = (left + right) / 2;
    if (searchnum < list[middle])
        return middle;
    else left = middle + 1;

//Compare Function
int compare(int x, int y){
  if(x < y) return -1;
  else if(x == y) return 0;
  else return 1;
}

// Compare Macro
#define COMPARE (x,y) ((x) < (y)) ? -1: ((x) == (y)) ? 0 : 1)

// Binary Search
int binsearch(int list[], int searchnum, int left, int right){
  int middle;
  while(left <= right){
    middle = (left + right) / 2;
    switch(COMPARE(list[middle], searchnum)){
      case -1: 
        left = middle + 1; 
        break;
      case 0: return middle;
      case 1: right = middle - 1;
    }
  }
  return -1;
}

---

2.2 재귀 알고리즘

• Direct recursion : 직접 순환. 함수가 그 수행이 완료되기 전에 자기 자신을 다시 호출

• Indirect recursion : 간접 순환. 호출 함수를 다시 호출하게 되어 있는 다른 함수를 호출

• [Binomial Coefficients] : 조합의 재귀적 표현

  $\left[ \begin{matrix} n \\ m \\ \end{matrix} \right] = {n!\over m!(n-m)!}$

  $\left[ \begin{matrix} n \\ m \\ \end{matrix} \right] = \left[ \begin{matrix} n-1 \\ m \\ \end{matrix} \right] + \left[ \begin{matrix} n-1 \\ m-1 \\ \end{matrix} \right]$

• [Fatorial] : 팩토리얼

  $n! = \begin{cases} n \times (n-1)! \quad if, \ n > 1\\ 1 \quad if,\ n = 1 \end{cases}$

• [Binary Search] : 이진 탐색

BSrch[key, left, right]
	if key < list[middle]
    	BSrch[key, left, middle-1]
    if key = list[middle]
    	list[middle]
    if key > list[middle]
    	BSrch[key, middle+1, right]

// 이진 탐색 재귀적 구현
int binsearch(int list[], int searchnum, int left, int right){
  int middle;
  if(left <= right){
    middle = (left + right) / 2;
    switch(COMPARE(list[middle], searchnum)){
      case -1: 
        return binsearch(list, searchnum, middle + 1, right);
      case 0: return middle;
      case 1: 
        return binsearch(list, searchnum, left, middle - 1);
    }
  }
  return -1;
}

• [Fibonacci Number] : 피보나치 수열

fn = 0 (if n = 0)
fn = 1 (if n = 1)
fn = fn-1 + fn-2 (if n > 1)

// 일반 함수
int fibo(int n){
	int g, h, f, i;
    if(n>1){
    	g = 0;
        h = 1;
        for(i = 2; i <= n; i++){
        	f = g + h;
            g = h;
            h = f;
        }
    }
    else f = n;
    return f;
}

// 재귀 함수
int rfibo(int n){
	if(n > 1) 
    	return rfibo(n-1) + rfibo(n-2);
    else return n;
}

• [Permutations] : 순열 생성

// 순열의 재귀적 생성
void perm(char *list, int i, int n){
  int j, temp;
  if(i == n){
    for(j = 0; j <= n; j++)
      printf("%c", list[j]);
    printf("\n");
  } else {
  	// list에 1개 이상의 문자가 들어있으면 재귀적으로 생성
    for(j = i; j <= n; j++){
      SWAP(&list[i], &list[j]);
      perm(list, i + 1, n);
      SWAP(&list[i], &list[j]);
    }
  }
}

---

3. Data Abstraction

• 데이터 타입 : 객체(object)와 그 객체를 가지고 하는 연산(operation)들의 모음

  • C의 기본 데이터 타입 : char, int, float, double ...
  • 여러 데이터를 grouping : array, struct
  • pointer 타입

• 추상 데이터 타입(ADT, Abstract Data Type) : 객체와 연산의 명세가 구현으로부터 분리된 데이터 타입.
  → 내부적 표현 or 구현에 대한 설명이 필요 없음

  • ADT 가 가지는 함수의 종류
    1. 생성자(creater)/구성자(constructor) : 지정된 타입에 맞는 새로운 인스턴스 생성
    2. 변환자(transformer) : 1개 이상의 다른 인스턴스를 사용해 지정된 타입의 한 인스턴스 만듬.
    3. 관찰자(observers)/보고자(reporter) : 인스턴스에 대한 정보 제공. 변화는 X

• [ADT Natural_Number ]

  Object : 0에서 시작해서 컴퓨터상의 최대 정수 값(INT_MAX)까지 순서화된 정수의 부분 범위
  Function:
     Nat_Number의 모든 원소 x,y 그리고 Boolean의 원소 T
     NaturalNumber Zero() ::= 0
     Boolean IsZero(x) ::=
         if (x) return FALSE
         else return TRUE
     Boolean Equal(x,y) ::=
         if(x==y) return TRUE
         else return FALSE
     NaturalNumber Successor(x) ::=
         if(x == INTMAX) return x
         else return x+1
     _NaturalNumber Add(x,y) ::=
         if((x+y) <= INT_MAX) return x+y
         else return INT_MAX
     NaturalNumber Subtract ::=
         if(x<y) return 0
         else return x-y

• 자세한 구현을 피하기 위해 ADT 사용

---

4. Performance Analysis

성능 분석의 기준

1. 프로그램이 원래의 명세와 부합하는가?
2. 정확하게 작동하는가?
3. 프로그램을 어떻게 사용하고 어떻게 수행하는지에 관한 문서화가 프로그램 내에 되어져 있는가?
4. 논리적 단위를 생성하기 위해 프로그램이 함수를 효과적으로 사용하는가?
5. 프로그램 코드는 읽기 쉬운가?

• 성능 분석

6. 프로그램이 메인 메모리와 보조기억장치를 효율적으로 사용하는가?
7. 작업에 대한 프로그램의 실행 시간은 허용할 만한가?

• Performance Analysis : 기계와 독립적인 시간 & 공간에 대해 평가
• Performace Measurement : 기계와 독립적이지 않은(의존적인) running time 계산. 비효율적인 코드 찾을 때 사용

4.1 공간 복잡도

• Fixed space requirement : 고정 공간 요구. 프로그램 입출력의 횟수나 크기와 관계 없는 공간 요구

  • 명령어 공간, 단순 변수, 고정 크기의 구조화 변수, 상수 등.

• Variable space requirement : 특정 인스턴스에 의존하는 크기를 가진 구조화 변수의 공간

• 전체 프로그램이 필요한 공간 : 고정 공간 + 가변 공간

  $S(P) = c + S_P(I)$

  → 공간 복잡도 분석시에는 가변 공간 요구에만 관심 가짐.

• 공간 복잡도 구하는 예시

// 단순 산술 함수
float abc(float a, float b, float c){
  return a+b+b*c+(a+b-c)/(a+b)+4.0;

→ $S_{abc}(I) = 0$

// 리스트에 있는 수를 합산하기 위한 반복 함수
float sum(float list[], int n){
  int i;
  float tempSum = 0;
  for(i = 0; i < n; i++)
    tempSum += list[i];
  return tempSum;
}

→ $S_{n}(I) = 0$ : 인자가 pass-by-reference일 때(포인터로 전달)
→ $S_{n}(I) = n$ : 인자가 pass-by-value일 때(전체 배열 복사)

// 리스트에 있는 수를 합산하기 위한 순환 함수
float rsum(float list[], int n){
  if(n) return rsum(list, n-1) + list[n-1];
  return 0;
}

→ 같은 함수라도 순환 함수로 구현하면 공간 요구가 더 커짐.

---

4.2 시간 복잡도

• 소요되는 총 시간 : 컴파일 시간 + 실행 시간

  $T(P) = c + T_p(I)$

  → 시간 복잡도 분석시에는 실행 시간에만 관심 가짐.

• 프로그램 단계 program step : 실행 시간이 인스턴스 특성에 구문적으로 / 의미적으로 독립성을 갖는 프로그램의 단위

• 시간 복잡도 구하는 예시

// 리스트에 있는 수를 합산하기 위한 반복 함수
float sum(float list[], int n){
  int i;
  float tempSum = 0;
  for(i = 0; i < n; i++)
    tempSum += list[i];
  return tempSum;
}

→ 2n + 3

• 단계 수 테이블 방식 : 명령문에 대한 단계수(s/e, steps/execution), 빈도수(명령문이 수행되는 횟수, frequency)
  • s/e * 빈도수 = 총 단계 수 (total steps)
  • 

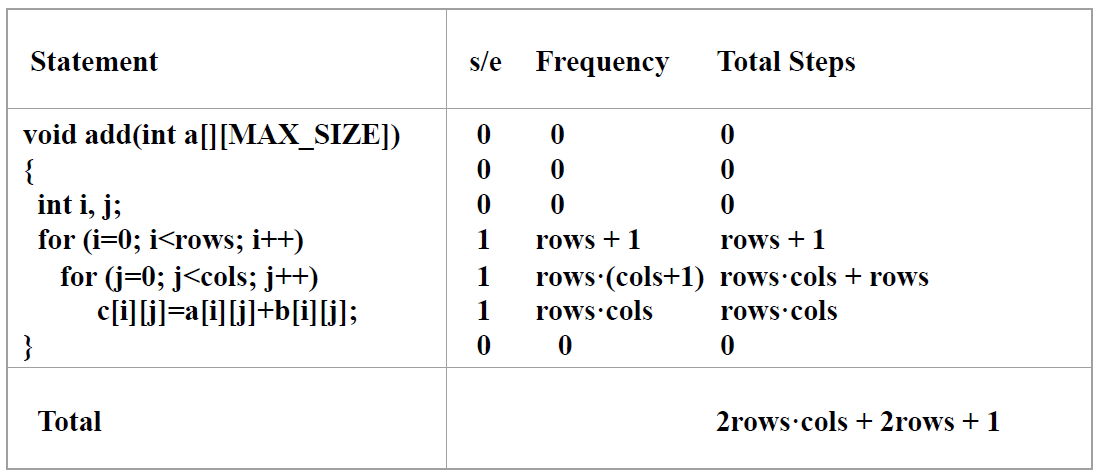
• 같은 함수라도 case에 따라 step count가 다를 수 있다.

---

4.3 Asymptotic Notation (O, $\Omega$, $\Theta$)

• Step count를 직접 구하는 대신 점근 표기법 사용

Big-O Notation

f(x) = O(g(x))
↔ x > k 일 때 항상 $|f(x)| \leq C|g(x)|$ 를 만족하는 상수 C와 k 가 존재한다.

• 최고 차항만 남기기
• Big-O의 예시
  • 3n + 2 = O(n)
  • 10n2 + 4n + 2 = O(n2)
  • 6 $\cdot$ 2n + 4n2 + 2 = O(2n)
    

Big-Omega

f(x) = $\Omega$(g(n))
↔ x > k 일 때 항상 $|f(x)| \geq C|g(x)|$ 를 만족하는 상수 C와 k 가 존재한다.

• 빅오가 상한값이하면, 오메가는 하한값.
• 작은 것 중 가장 큰 것.
• Big-$\Omega$의 예시
  • 3n + 2 = $\Omega$(n)
  • 10n2 + 4n + 2 = $\Omega$(n2)
  • 6 $\cdot$ 2n + 4n2 + 2 = $\Omega$(2n)

Big-Theta

f(x) = $\Theta$(g(n))
↔ f(x) = O(g(x)) && f(x) = Ω(g(x))

• Big-$\Theta$의 예시
  • 3n + 2 = $\Theta$(n)
  • 10n2 + 4n + 2 = $\Theta$(n2)
  • 6 $\cdot$ 2n + 4n2 + 2 = $\Theta$(2n)

시간 복잡도 구하기

• [Matrix addition]

void add(int a[][MAX_SIZE] ...){
	int i, j;
    for(i = 0; i < rows; i++)
    	for(j = 0; j < cols; j++)
        	c[i][j] = a[i][j] + b[i][j];
}

→ 시간 복잡도 : $\Theta$(rows * cols)

• [Binary Search]
  → 시간 복잡도 : $\Theta$(log n)
  • best case : $\Theta$(1)
• [Magic Square]

// 매직 스퀘어 프로그램
int main(void){
  // 정방형을 반복적으로 생성
  int square[MAX_SIZE][MAX_SIZE];
  int i, j, row, column;  // 지수
  int count; // 계수
  int size; // 정방형의 크기

  printf("Enter the size of the square: ");
  scanf("%d", &size);

  // 입력에 오류가 있는지 체크
  if(size < 1 || size > MAX_SIZE + 1){
    fprintf(stderr, "Error! Size is out of range\n");
    exit(1);
  }
  if(!(size % 2)){
    fprintf(stderr, "Error! Size is even\n");
    exit(1);
  }

  for (i=0; i<size; i++)
    for(j=0; j<size; j++)
      square[i][j] = 0;
  square[0][(size - 1) / 2] = 1; // 첫 번째 행의 중앙에 1 넣기
  // i와 j는 현재 위치
  i = 0;
  j = (size - 1) / 2;
  for(count = 2; count <= size * size; count++){
    // 다음 위치 계산
    row = (i - 1 < 0) ? size - 1 : i - 1;  // 위로
    column = (j - 1 < 0) ? size - 1 : j - 1;  // 왼쪽으로
    // 이미 채워져 있는지 확인
    if(square[row][column]){  // 아래로
      i = (++i) % size;
    }
    else{  // 정방형이 비어있을 경우
      i = row;
      j = column;
    }
    square[i][j] = count;
  }
  // 정방형 출력
  printf("\nMagic Square of size %d: \n\n", size);
  for(i = 0; i < size; i++){
    for(j = 0; j < size; j++)
      printf("%5d", square[i][j]);
    printf("\n");
  }
  printf("\n\n");
}

시간 복잡도 : $\Theta$(n2)

---

4.4 실용적 복잡도

---

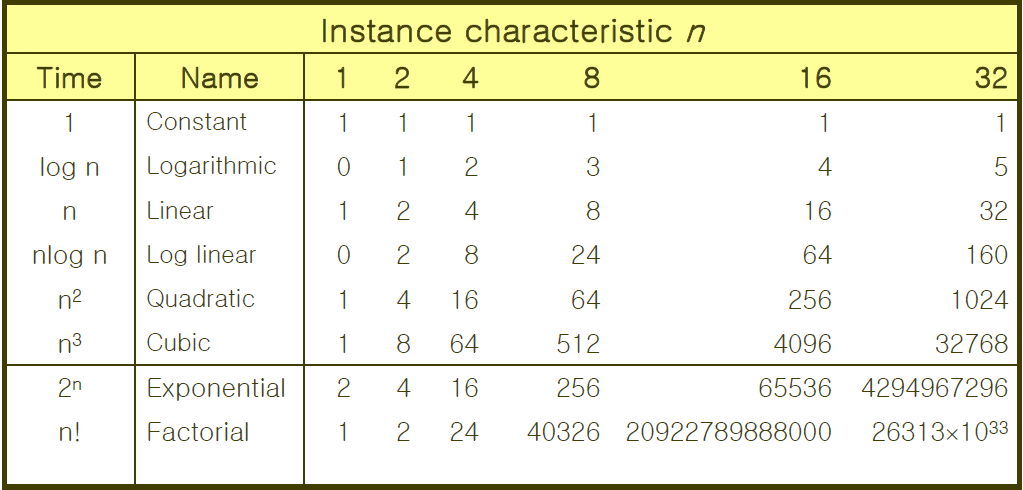
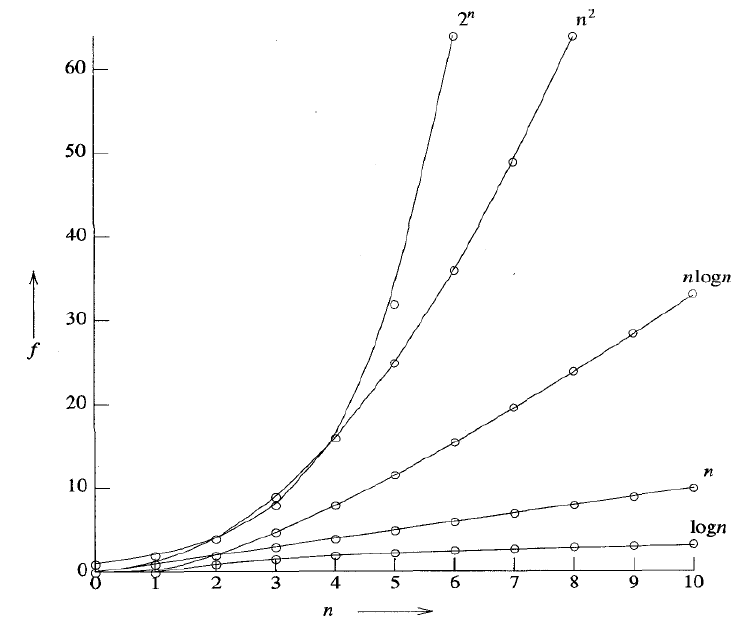
5. Performance Measurement

• 시간 측정 방법 : <time.h> 사용

	Method1	Method2
Start Timing	Start = clock();	Start = time(NULL);
Stop Timing	Stop = clock();	Stop = time(NULL);
Type returned	Clock_t	Time_t
Result in second	Duration = ((double)(Stop-Start))/CLOCKS_PER_SEC;	Duration=(double)difftime(Stop,Start)