그래프 알고리즘 Graph Algorithm

그래프란?

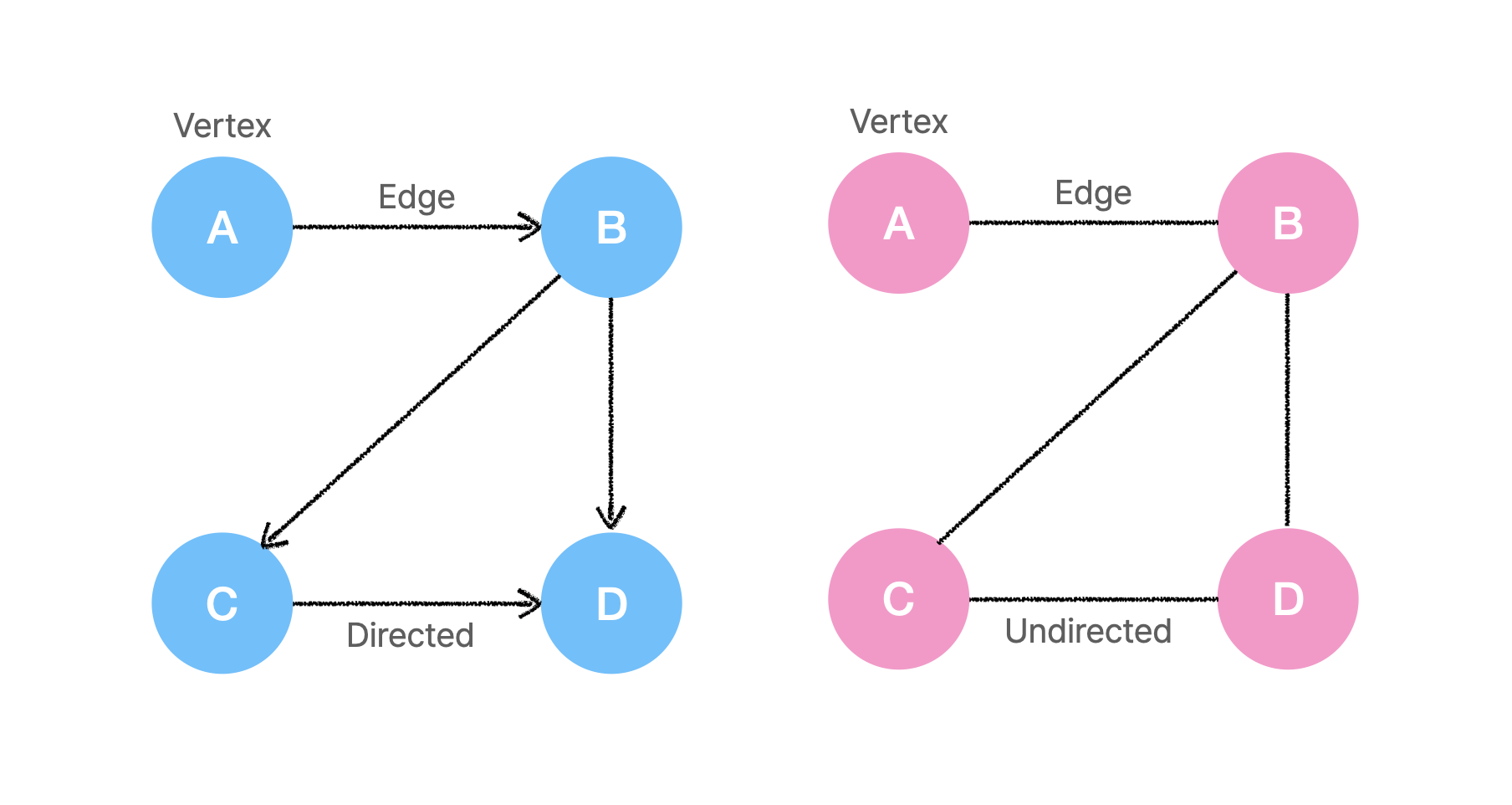
일반적으로 정점(Vertex, Node)과 간선(Edge, Link)으로 이루어진 자료구조를 말한다.
간선의 방향 유무에 따라 단방향(Directed) 그래프와 양방향(Undirected) 그래프로 나눌 수 있다.

그래프 표현

1. 인접 행렬 Adjacency Matrix

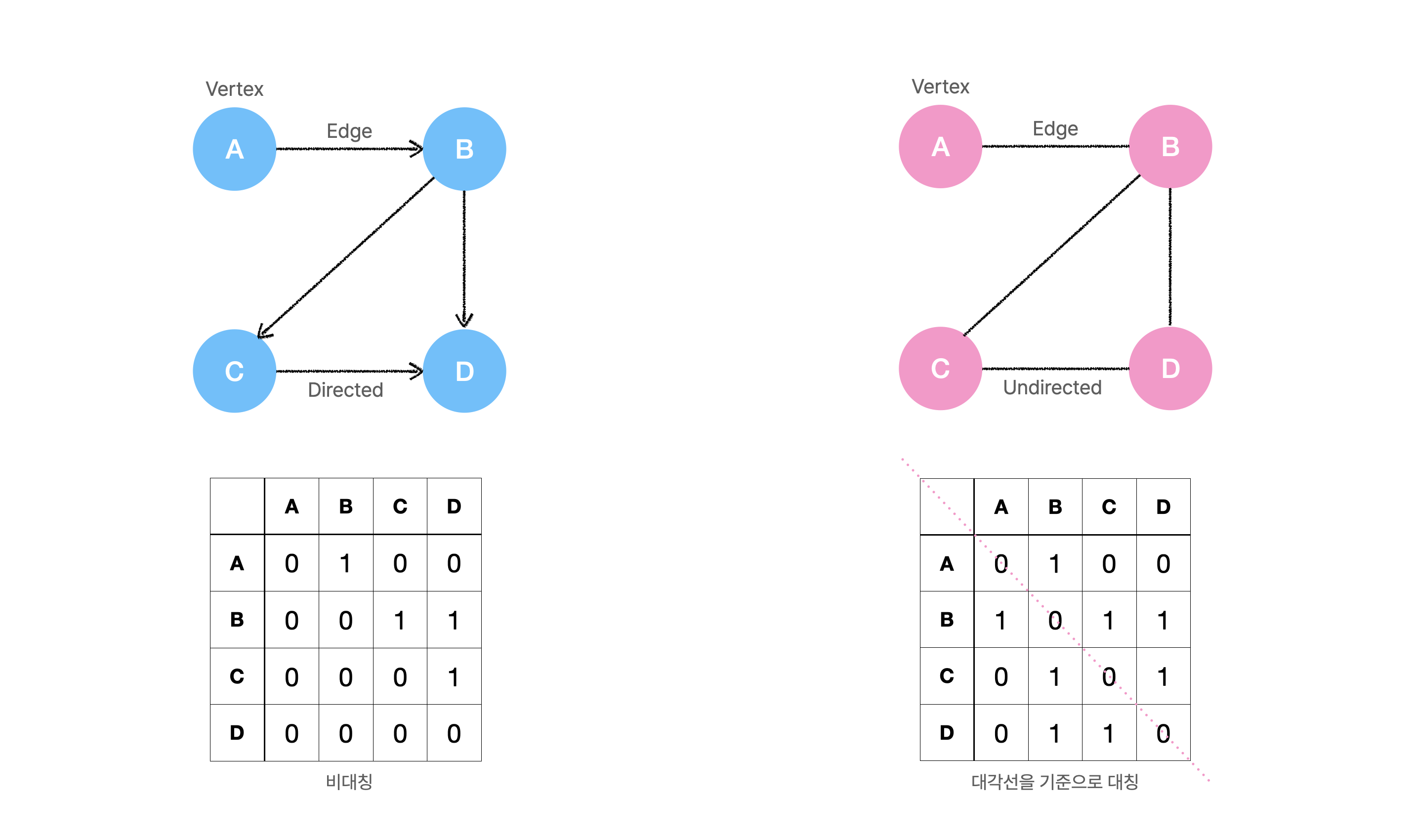
• 특징 : 모든 정보를 저장한다.
• 장점 : 직관적이며 상대적으로 구현하기 쉽다.
• 단점 : 불필요한 정보도 저장하며, 그래프의 크기가 커지면 메모리 초과가 발생할 가능성이 크다.
• 구현 : 주로 int type의 2차원 배열을 사용하여 구현하며, 이동할 수 있으면 1 없으면 0으로 표시한다.
• 저장 공간 : O(n^2) (n = vertex)

2. 인접 리스트 Adjacency List

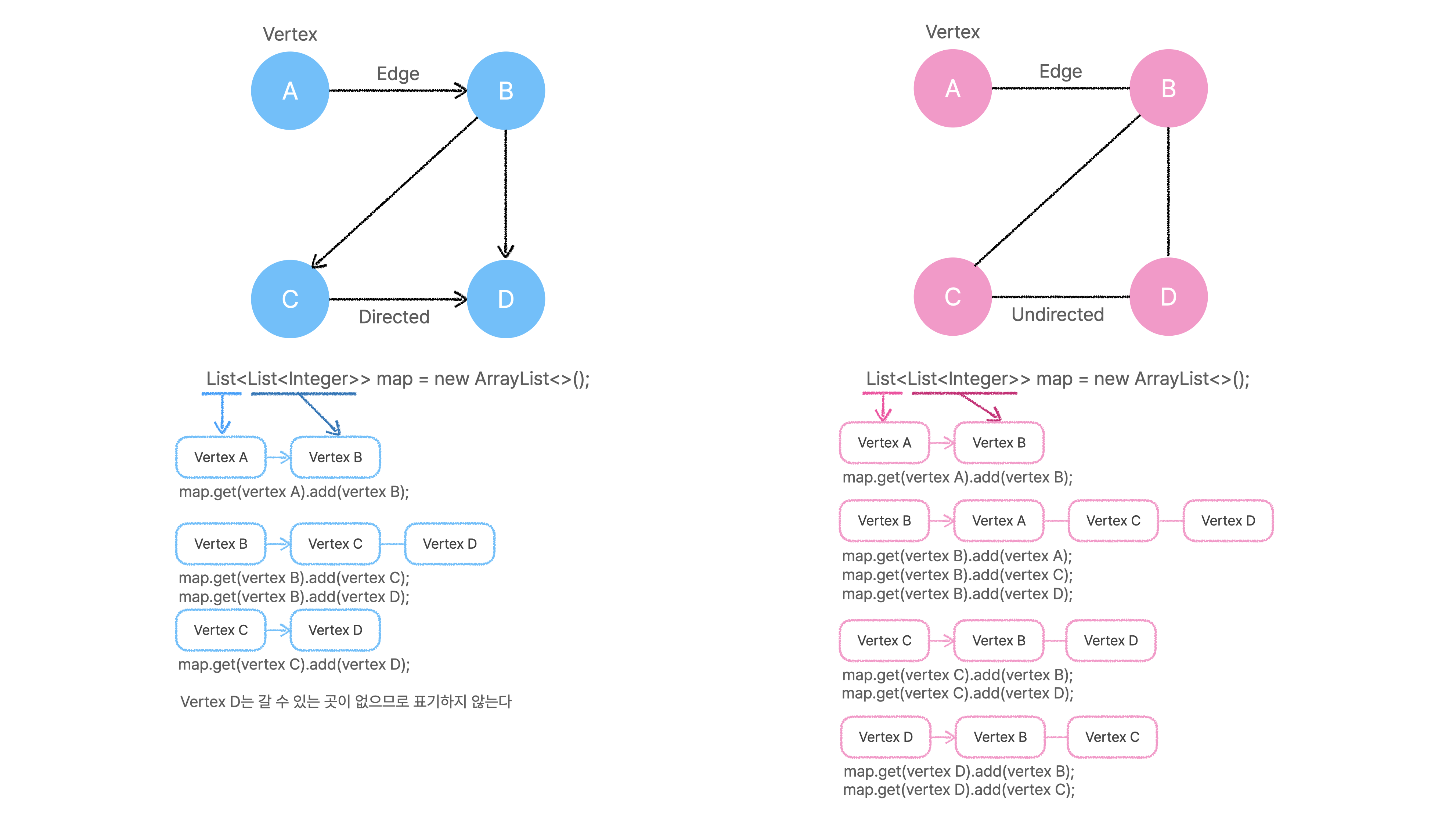
• 특징 : 갈 수 있는 곳만 저장한다.
• 장점 : 필요한 정보만 저장하여 메모리의 크기를 줄일 수 있다.
• 단점 : 인접 행렬에 비해 상대적으로 구현하기 어렵다.
• 구현 : 주로 List 를 사용하여 각 정점에서 이동 가능한 정점들을 저장한다.
• 저장 공간 : O(n+m) (n = vertex, m = edge)

그래프 탐색

1. 기법

1. Breadth-First Search 넓이 우선 탐색
   Queue를 이용해서 구현하며 BFS는 트리 탐색의 Level Order와 동일하다.

BFS와 DFS 관련 문제 : 백준 1206번 DFS와 BFS

import collections


def dfs(graph, start_node):  # 깊이 우선 탐색 함수 구현
    visited[start_node] = True
    print(start_node, end=" ")

    for node in graph[start_node]:
        if not visited[node]:
            dfs(graph, node)  # 재귀 방식 사용


def bfs(graph, start_node):  # 넓이 우선 탐색 함수 구현
    queue = collections.deque([start_node])  # Queue 사용하여 구현
    visited[start_node] = True

    while queue:
        node = queue.popleft()
        print(node, end=" ")

        for vertex in graph[node]:
            if not visited[vertex]:
                queue.append(vertex)
                visited[vertex] = True


# 문제 풀이
node, edge, start_node = map(int, input().split())

graph = [[] for _ in range(node + 1)]

for _ in range(edge):
    node1, node2 = map(int, input().split())
    graph[node1].append(node2)
    graph[node2].append(node1)

for graph_list in graph:
    graph_list.sort()

visited = [False] * (node + 1)
dfs(graph, start_node)

print()

visited = [False] * (node + 1)
bfs(graph, start_node)

2. Depth-First Search 깊이 우선 탐색
   관련된 알고리즘으로는 백트래킹이 있다. Stack을 이용해서 구현하며, 직접 스택을 구현하거나 시스템 스택을 사용하는 재귀 호출을 사용할 수 있다. 트리 탐색의 Inorder와 동일하다.

DFS 관련 문제 : 백준 13023번 ABCDE

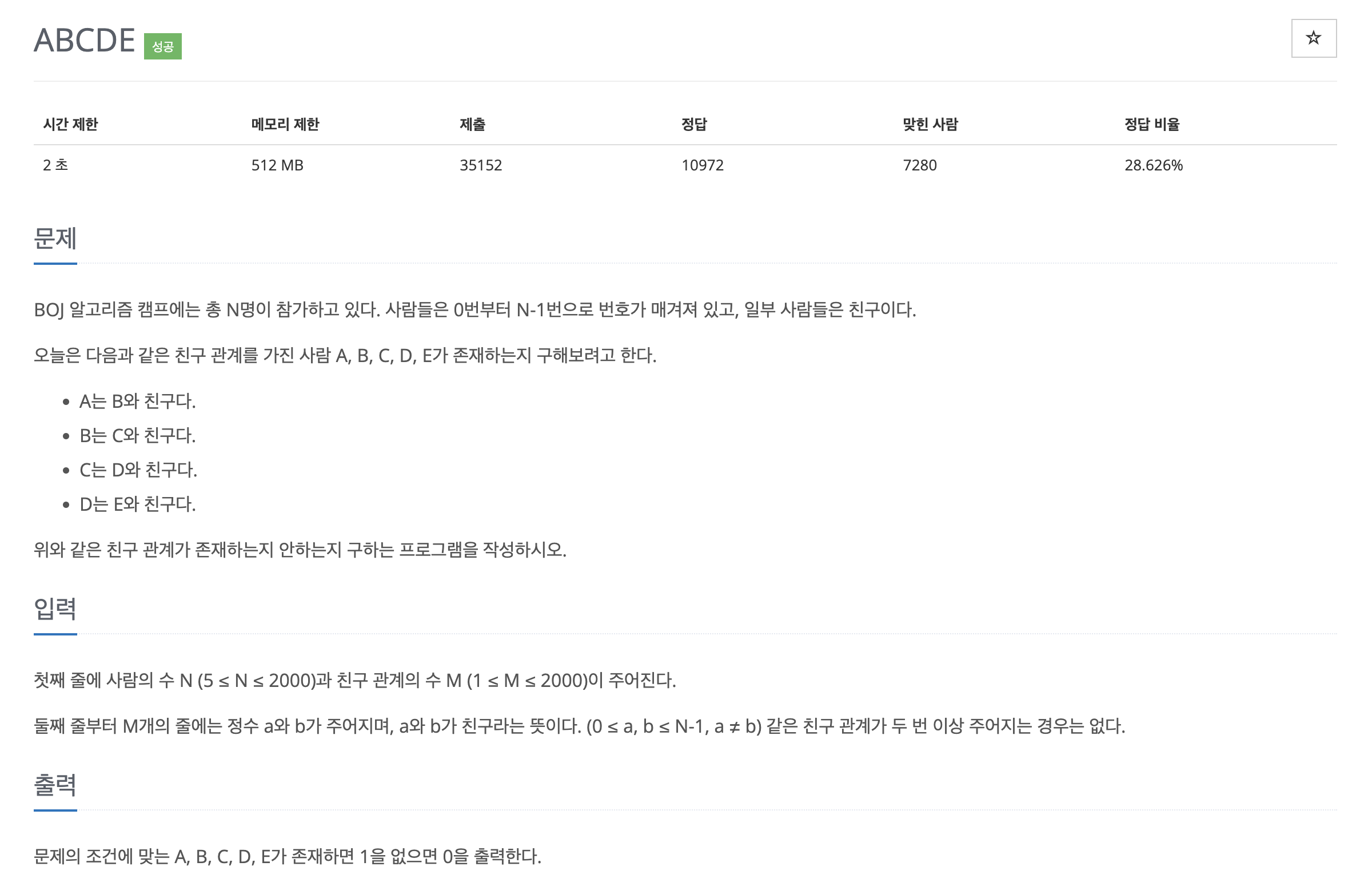
# N : 사람의 수
# M : 친구 관계의 수
N, M = map(int, input().split())

# 친구 관계의 수가 4개 미만이면 0을 출력하고 종료한다.
if M < 4:
    print(0)
    exit()

# 리스트 초기화
graph = [[] for _ in range(N)]

# 방문 유뮤를 확인하기 위한 리스트
visited = [False] * N

# 모든 경우의 수 저장하기
for _ in range(M):
    A, B = map(int, input().split())
    graph[A].append(B)
    graph[B].append(A)


# 재귀 함수 만들기
def dfs(node, depth):
    if depth == 4:
        print(1)
        exit()

    visited[node] = True
    for move in graph[node]:
        if not visited[move]:
            dfs(move, depth + 1)

    visited[node] = False


for i in range(N):
    dfs(i, 0)

print(0)

3. Dijkstra 다익스트라
   다익스트라 알고리즘은 어느 한 정점에서 모든 정점까지의 최단 경로를 찾는데 사용되며, 매 탐색마다 해당 정점까지의 가중치의 합을 최솟값으로 갱신하는 방식이다. 일반적으로 Queue 대신 Priority Queue를 사용하여 시간을 단축시킨다. 단, 음이 아닌 가중치에 대해서만 사용이 가능하다는 점에 유의해야 한다.

4. Floyd Warshall 플로이드 와샬
   다익스트라가 특정 정점에서 각 정점까지의 최단거리를 구하는 알고리즘이었다면 플로이드 와샬 알고리즘은 모든 정점에서 각 정점까지의 최단 거리를 구하는 알고리즘이다. 3중 For문을 이용하여 각 정점마다 다른 정점까지의 최단 거리를 모든 정점에 대해 구하기 때문에 모든 정점들의 최단 거리를 모두 파악할 수 있지만 O(V^3)의 시간이 걸린다. 그러나 양과 음의 모든 가중치에 대해 계산이 가능하고 4줄밖에 안되는 코드라는 단순함 때문에 자주 이용된다.

5. Kruskal 크루스칼
   크루스칼 알고리즘은 그래프 내의 모든 정점들을 가장 적은 비용으로 연결하기 위해 사용한다.
   그래프 내의 모든 정점을 포함하는 사이클이 없는 연결 선을 그렸으며, 가중치의 합이 최소가 되는 상황을 구하고 싶을 때 크루스칼 알고리즘을 사용할 수 있다. 즉, 최소 신장 트리를 구하기 위한 알고리즘이다.

최소 신장 트리란? Minimum Spanning Tree, MST
신장 트리는 (1) 그래프의 모든 정점을 포함하고, (2) 정점 간 서로 연결이 되며, (3) 사이클이 존재하지 않는 그래프를 말한다. 신장 트리들 중에서 가중치의 합이 최소가 되는 신장 트리를 최소 신장 트리라고 한다.

• 최소 신장 트리를 구하는 문제 예시
  • 여러 개의 네트워크 지점들이 존재할 때, 모든 지점들을 유선으로 연결하되 연결선의 총 길이가 최소가 되어야 하는 문제
  • 도시들을 모두 연결하되, 연결하는 도로 길이의 합이 최소가 되어야 하는 문제

2. 유형

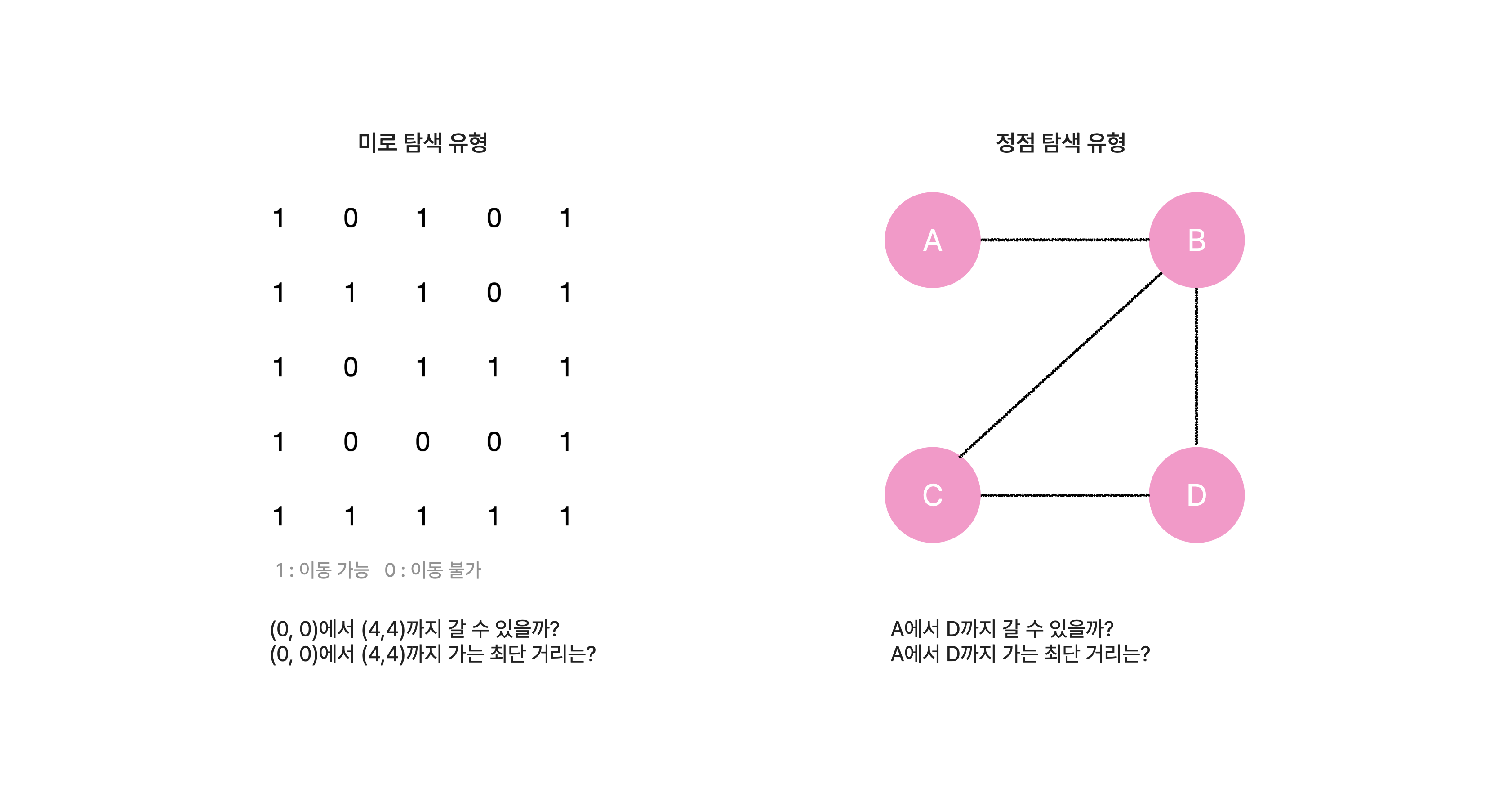
1. 미로 탐색 유형
   현재 좌표에서 상하좌우로 이동하면서 길을 찾아나가는 방식으로, 주로 인접 행렬 그래프가 주어진다.
   행렬을 그래프 표기로 이해하려 하기보다는 지도나 그림으로 바라보는 것이 편하다.

2. 정점 탐색 유형
   현재 정점에서 인접 정접으로 갈수 있는지에 대한 정보가 주어진다.
   정점의 방문 유무를 boolean 을 이용하여 체크하는 방식으로 탐색한다.