정렬이란 데이터를 정해진 기준에 따라 배치해 의미 있는 구조로 재설정하는 것
| 정렬 알고리즘 | 정의 | 시간 복잡도 평균값 |
|---|---|---|
| 버블 bubble | 데이터의 인접 요소끼리 비교하고, swap 연산을 수행하며 정렬하는 방식 | O(n^2) |
| 선택 selection | 대상에서 가장 크거나 작은 데이터를 찾아가 선택을 반복하면서 정렬하는 방식 | O(n^2) |
| 삽입 insertion | 대상을 선택해 정렬된 영역에서 선택 데이터의 적절한 위치를 찾아 삽입하면서 정렬하는 방식 | O(n^2) |
| 퀵 quick | pivot 값을 선정해 해당 값을 기준으로 정렬하는 방식 | O(nlogn) |
| 병합 merge | 이미 정렬된 부분 집합들을 효율적으로 병합해 전체를 정렬하는 방식 | O(nlogn) |
| 기수 radix | 데이터의 자릿수를 바탕으로 비교해 데이터를 정렬하는 방식 | O(kn) |
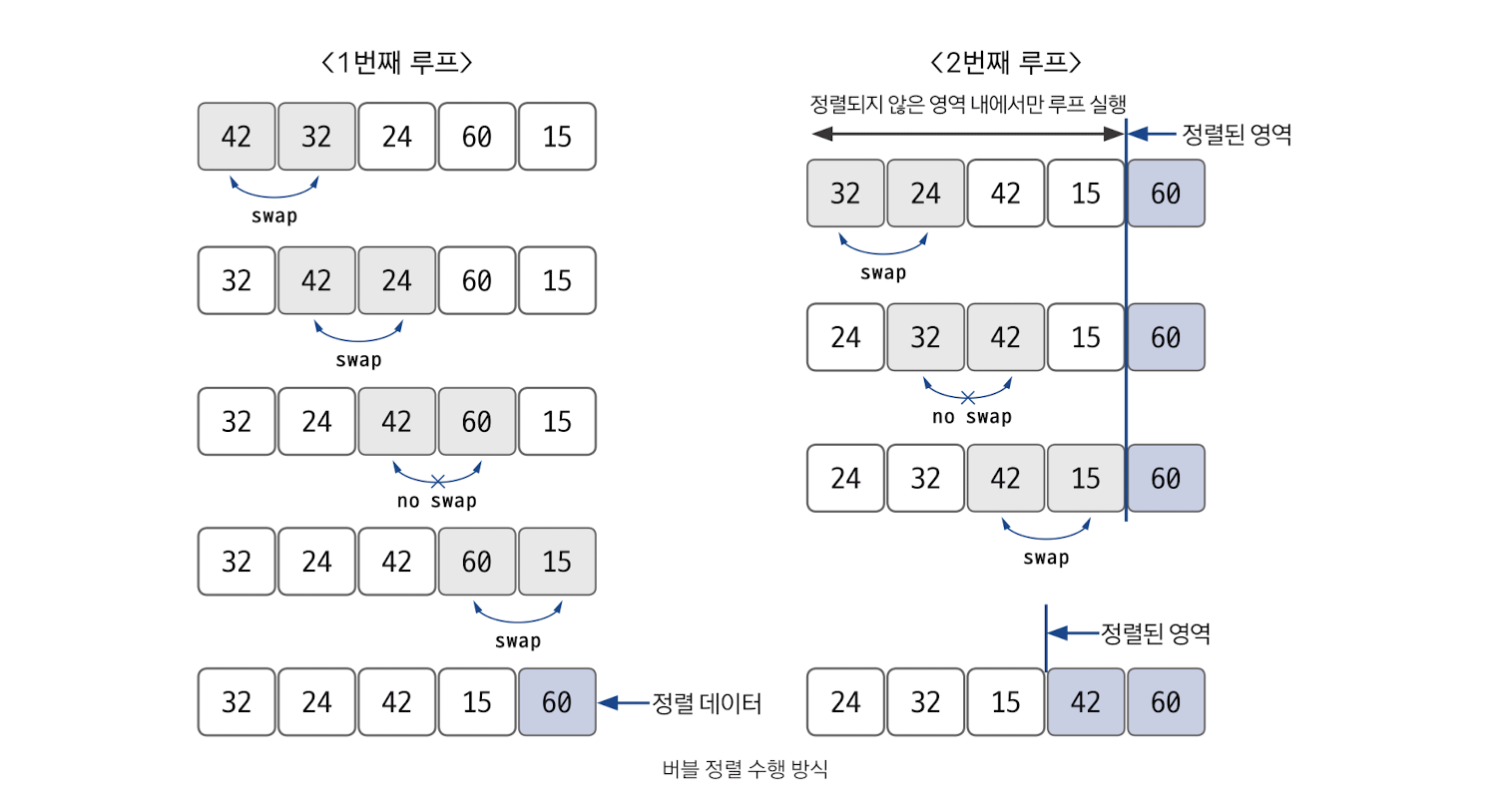
버블 정렬
간단하게 구현할 수 있지만, 배열 전체를 쭉 살펴보는 것을 n번 하기 때문에 시간 복잡도는 O(n^2)이다.
정렬 과정
-
비교 연산이 필요한 루프 범위를 설정한다.
-
인접한 데이터 값을 비교한다.
-
swap 조건에 부합하면 swap 연산을 수행한다.
-
루프 범위가 끝날 때까지 2~3을 반복한다.
-
정렬 영역을 설정한다. 다음 루프를 실행할 때는 이 영역을 제외한다.
-
비교 대상이 없을 때까지 1~5를 반복한다.
def bubblesort(A):
for i in range(1, len(A)):
for j in range(0, len(A) - 1):
if A[j] > A[j + 1]:
A[j], A[j + 1] = A[j + 1], A[j]선택 정렬
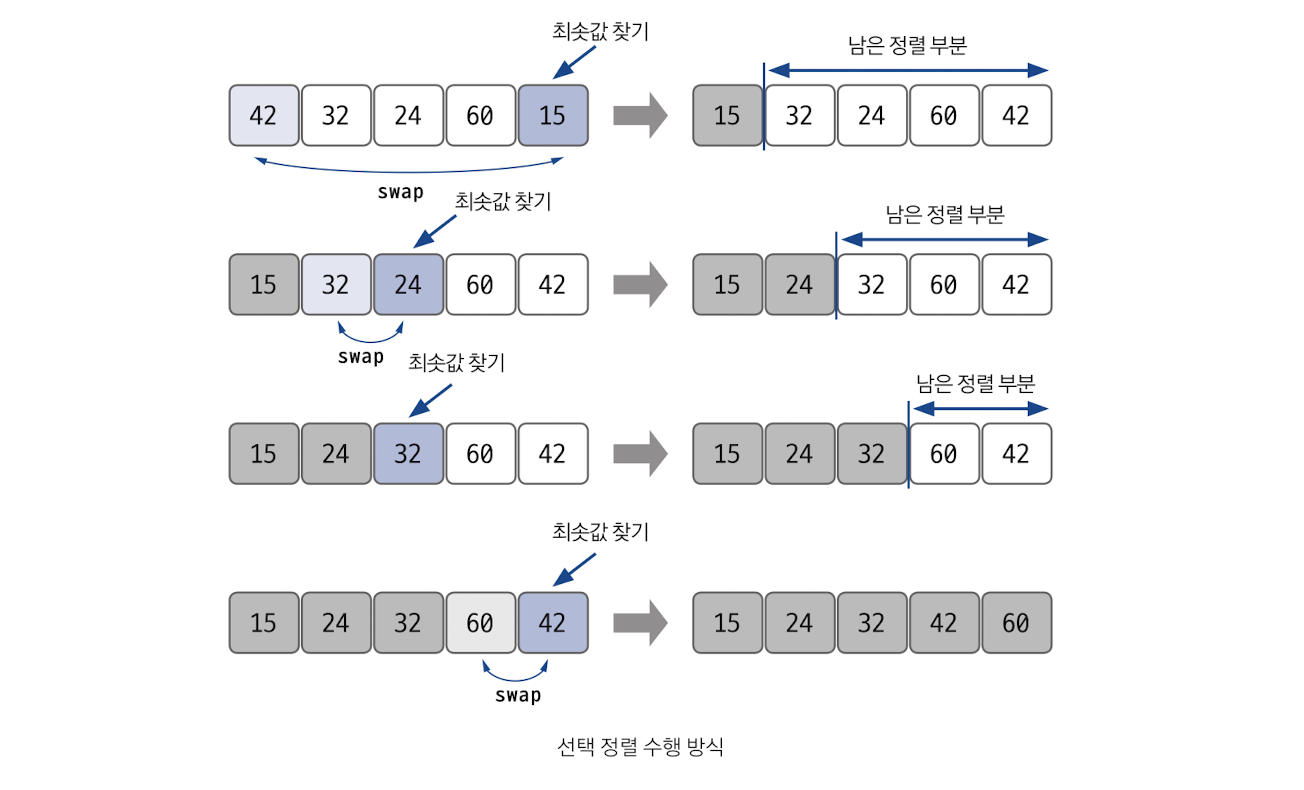
선택 정렬은 구현 방법이 복잡하고, 시간 복잡도도 O(n^2)으로 효율적이지 않아 코딩 테스트에서는 많이 사용하지 않지만 원리를 응용하는 문제는 나올 수 있다.
정렬 과정
-
남은 정렬 부분에서 최솟값 또는 최댓값을 찾는다.
-
남은 정렬 부분에서 가장 앞에 있는 데이터와 선택된 데이터를 swap한다.
-
가장 앞에 있는 데이터의 위치를 변경해(index++) 남은 정렬 부분의 범위를 축소한다.
-
전체 데이터 크기만큼 index가 커질 때까지, 즉 남은 정렬 부분이 없을 때까지 반복한다.
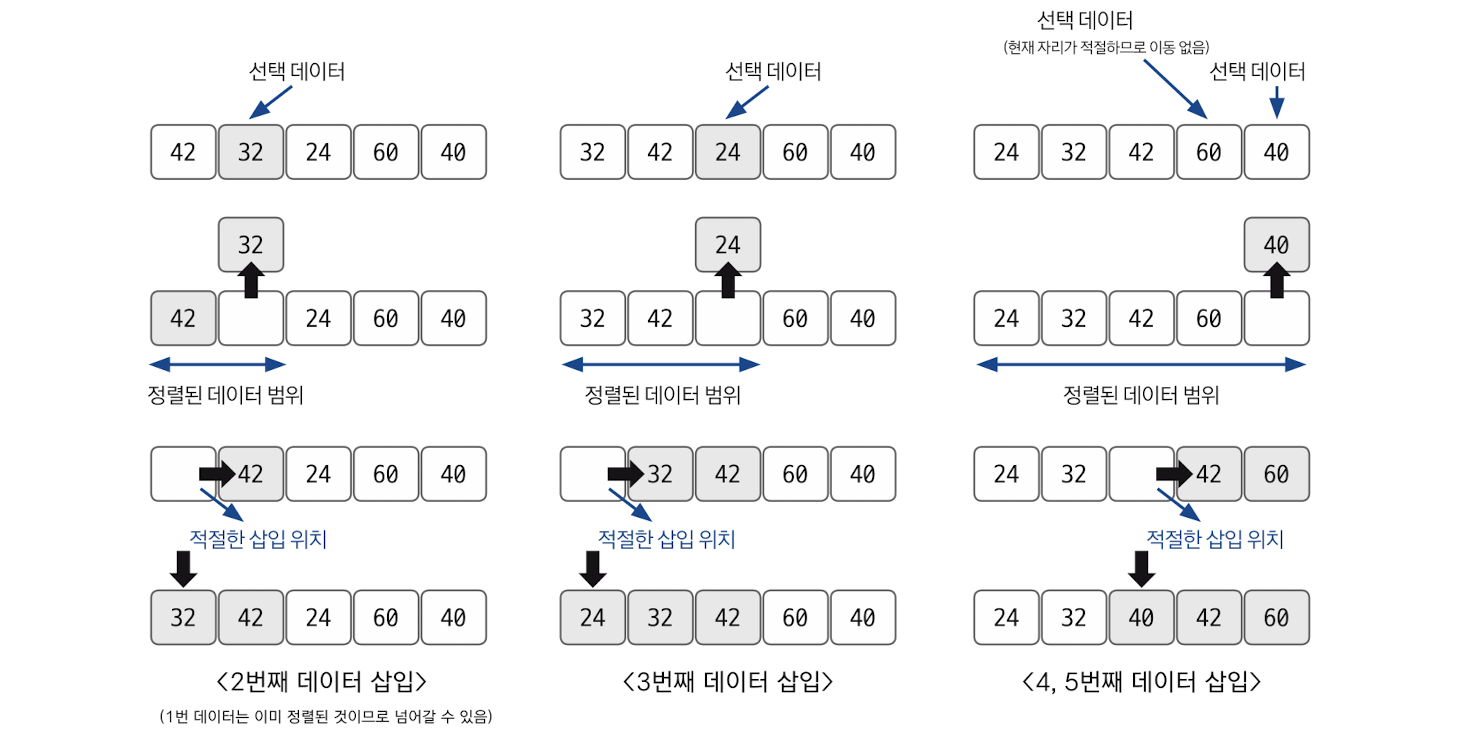
삽입 정렬
평균 시간 복잡도는 O(n^2)으로 느린 편이지만 구현하기 쉽다. 적절한 삽입 위치를 탐색하는 부분에서 이진 탐색 등과 같은 탐색 알고리즘을 사용하면 시간 복잡도를 줄일 수 있다.
정렬 과정
-
현재 index에 있는 데이터 값을 선택한다.
-
현재 선택한 데이터가 정렬된 데이터 범위에 삽입될 위치를 탐색한다.
-
삽입 위치부터 index에 있는 위치까지 shift 연산을 수행한다.
-
삽입 위치에 현재 선택한 데이터를 삽입하고 index++ 연산을 수행한다.
-
전체 데이터의 크기만큼 index가 커질 때까지, 즉 선택할 데이터가 없을 때까지 반복한다.
퀵 정렬
기준이 되는 값인 pivot이 어떻게 선정되는지가 시간 복잡도에 많은 영향을 미치며, 평균적인 시간 복잡도는 O(nlogn)이다. 재귀 함수의 형태로 구현해 볼 것을 추천한다.
정렬 과정
-
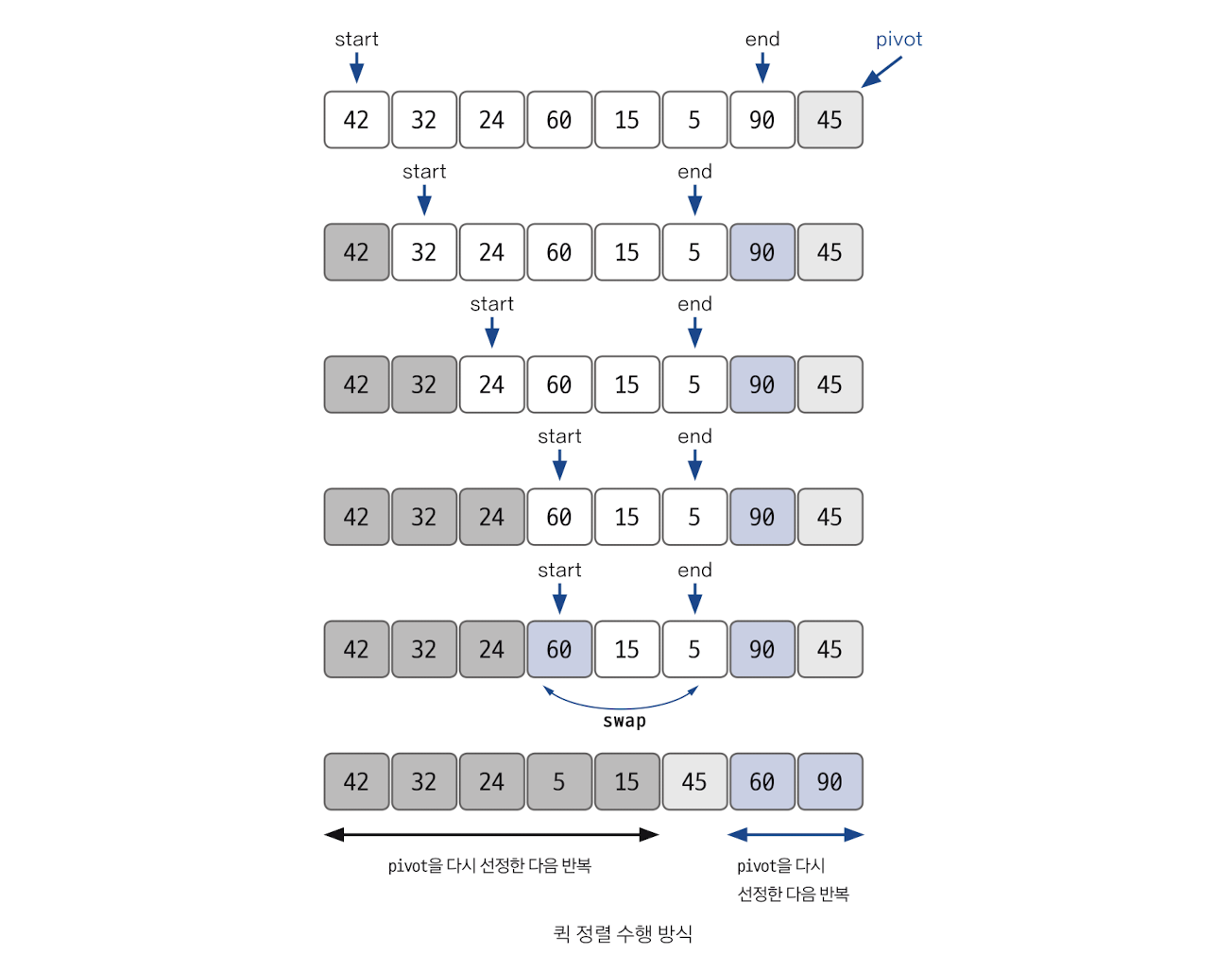
데이터를 분할하는 pivot을 설정한다(아래 그림의 경우 오른쪽 끝을 pivot으로 설정).
-
pivot을 기준으로 다음 a~e 과정을 거쳐 데이터를 2개의 집합으로 분리한다.
-
a. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start를 오른쪽으로 1칸 이동한다.
-
b. end가 가리키는 데이터가 pivot이 가리키는 데이터보다 크면 end를 왼쪽으로 1칸 이동한다.
-
c. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 크고, end가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start, end가 가리키는 데이터를 swap하고 start는 오른쪽, end는 왼쪽으로 1칸씩 이동한다.
-
d. start와 end가 만날 때까지 a~c를 반복한다.
-
e. start와 end가 만나면 만난 지점에서 가리키는 데이터와 pivot이 가리키는 데이터를 비교하여 pivot이 가리키는 데이터가 크면 만난 지점의 오른쪽에, 작으면 만난 지점의 왼쪽의 pivot이 가리키는 데이터를 삽입한다.
-
-
분리 집합에서 각각 다시 pivot을 설정한다.
-
분리 집합이 1개 이하가 될 때까지 과정 1~3을 반복한다.
병합 정렬
분할 정복 방식을 사용해 데이터를 분할하고 분할한 집합을 정렬하며 합치는 알고리즘이다. 최선과 최악 모두 O(n log n)의 시간 복잡도를 갖는다. 대부분의 경우 퀵 정렬보다는 느리지만 일정한 실행 속도를 갖는 것 뿐만 아니라 안정 정렬이라는 점에서 상용 라이브러리에 많이 쓰이고 있다.
정렬 과정
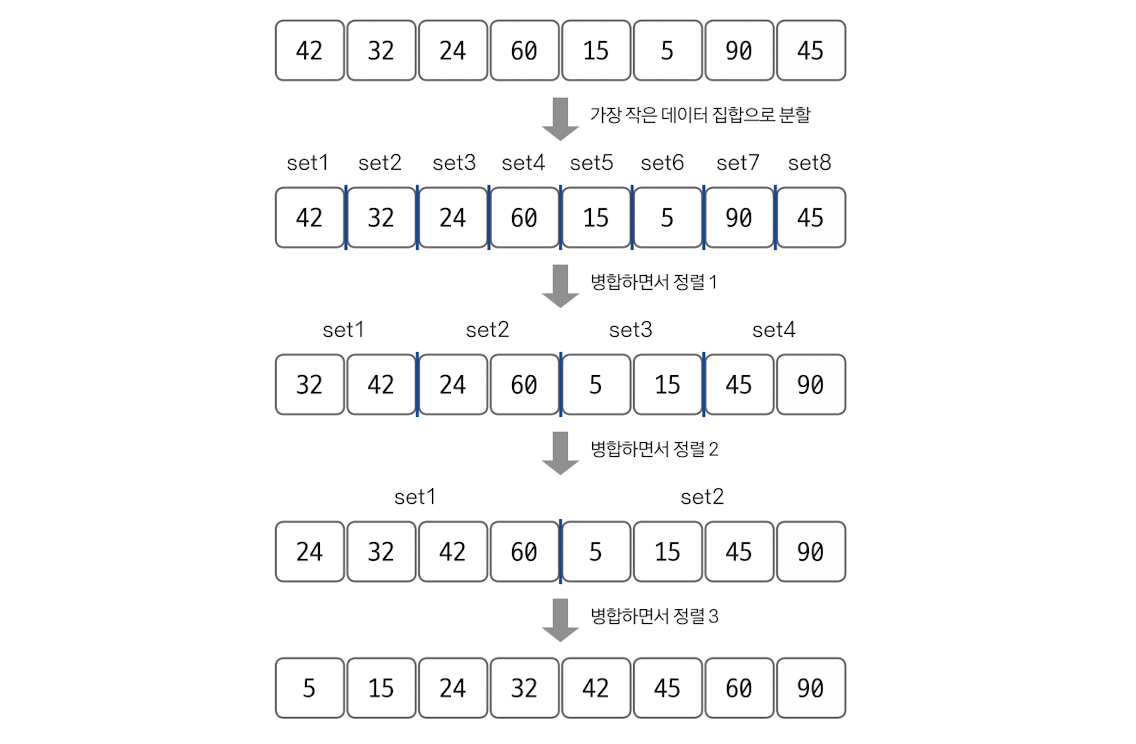
2개의 그룹을 병합하는 과정을 반복한다.
아래의 그림을 보면 최초에는 8개의 그룹으로 나누고, 2개씩 그룹을 합치며 오름차순으로 정렬한다. 그 결과 (32, 42), (24,60), (5, 15), (45, 90)이 된다. 이어서 계속 2개씩 그룹을 합치면서 다시 오름차순으로 정렬한다.
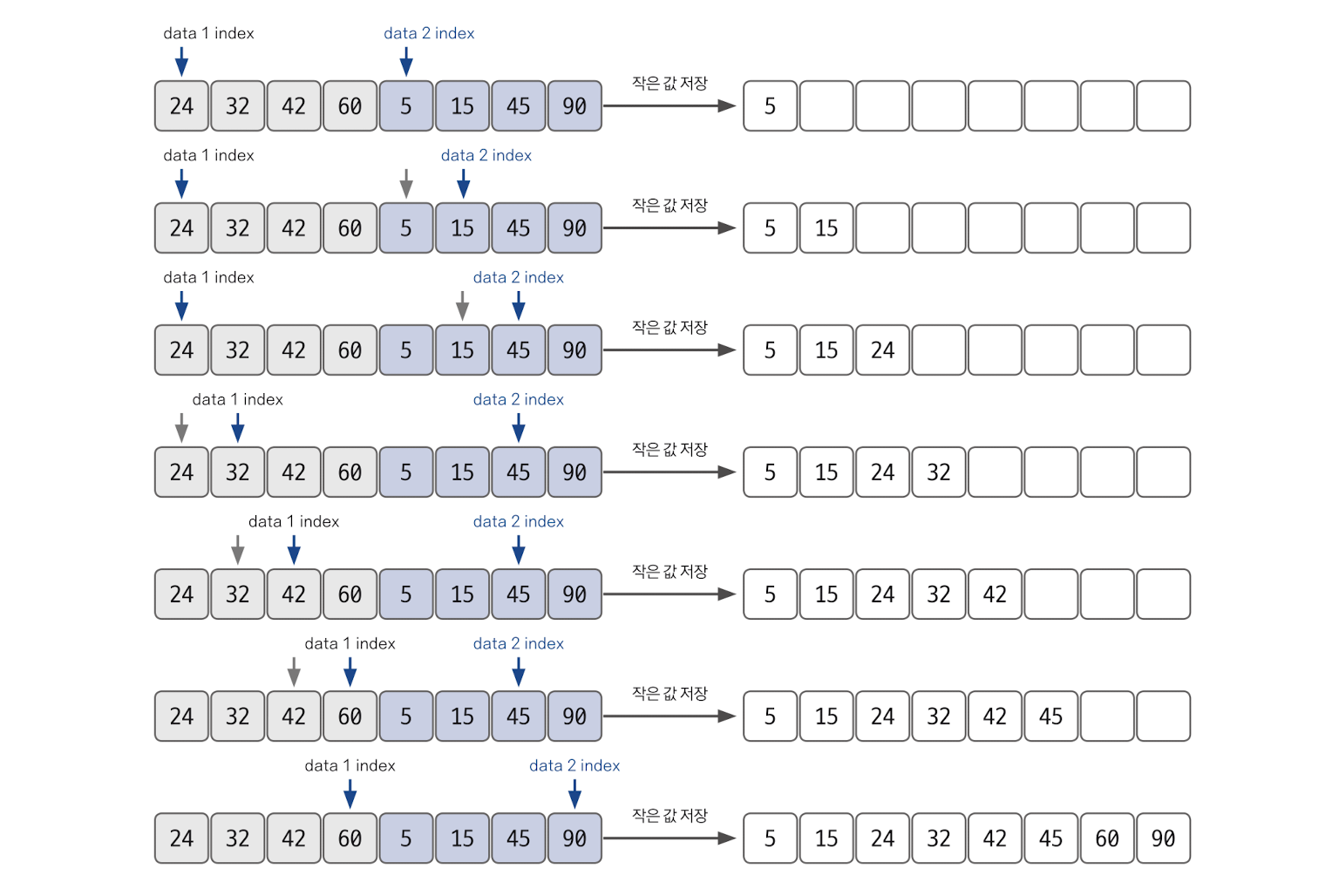
이때, 투 포인터 개념을 사용하여 왼쪽과 오른쪽 그룹을 병합한다. 왼쪽 포인터와 오른쪽 포인터의 값을 비교하여 작은 값을 결과 배열에 추가하고 포인터를 오른쪽으로 1칸 이동한다. 이 과정을 반복하여 2개의 그룹을 하나로 병합한다.
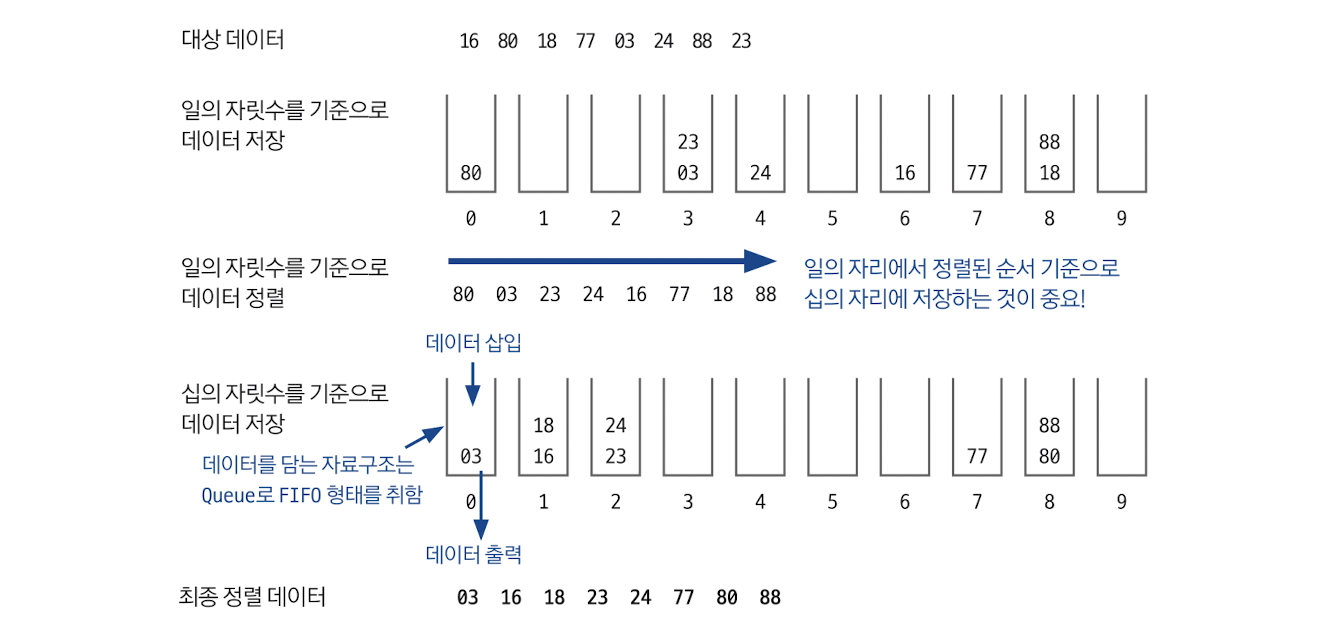
기수 정렬
값을 비교하지 않는 특이한 정렬 방식으로, 비교할 자릿수를 정한 다음 해당 자릿수만 비교한다. 기수 정렬의 시간 복잡도는 O(kn)으로 시간 복잡도가 가장 짧은 정렬이다. 여기서 k는 데이터의 자릿수를 말한다.
정렬 과정
기수 정렬은 10개의 큐를 이용한다. 각 큐는 자릿수의 값을 대표한다.
-
일의 자릿수를 기준으로 원소를 큐에 집어 넣는다.
-
0번째 큐부터 9번째 큐까지 pop을 진행한다.
-
이어서 십의 자릿수를 기준으로 같은 과정을 진행한다.
-
마지막 자릿수를 기준으로 정렬할 때까지 앞의 과정을 반복한다.