✍ 문제
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오.
수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
✍ 입력
첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다.
행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.
✍ 출력
첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.
✅ 코드
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
using matrix = vector<vector<int>>;
matrix result, mt;
matrix mul(matrix mt1, matrix mt2) { //두 행렬 사이의 곱
int size = mt1.size();
matrix result;
for (int i = 0; i < size; i++) {
vector<int> row;
for (int j = 0; j < size; j++) {
int temp = 0;
for (int k = 0; k < size; k++) temp += mt1[i][k] * mt2[k][j];
row.push_back(temp % 1000);
}
result.push_back(row);
}
return result;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, temp;
long long power;
cin >> n >> power;
result.resize(n, vector<int>(n,0));
for (int i = 0; i < n; i++) {
vector<int> row;
for (int j = 0; j < n; j++) {
cin >> temp;
row.push_back(temp);
}
mt.push_back(row);
result[i][i] = 1;
}
while (power > 0) { //분할정복을 이용한 거듭제곱 계산
if (power % 2 == 1) result = mul(result, mt);
power /= 2;
mt = mul(mt, mt);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << result[i][j] << ' ';
}
cout << '\n';
}
return 0;
}✅ 코드풀이
❗ 알고리즘
10830번에서 어떤 행렬의 거듭제곱 값을 구할 때, 단순 곱셈만을 사용하여 순차적으로 계산하면 시간복잡도가 O(N)이 되어 시간 초과에 걸리게 된다. 이 문제에서 지수의 최대 값이 100,000,000,000 무려 천 억이므로 시간 초과가 나는 것이 당연하다.
따라서 우리는 O(N) 보다 효율적인 방법을 찾아야 하는데, 이 때 사용하는 것이 "분할 정복" 알고리즘이다. 분할 정복을 사용하게 되면 O(logN)의 시간복잡도로 문제를 해결할 수 있게 된다.
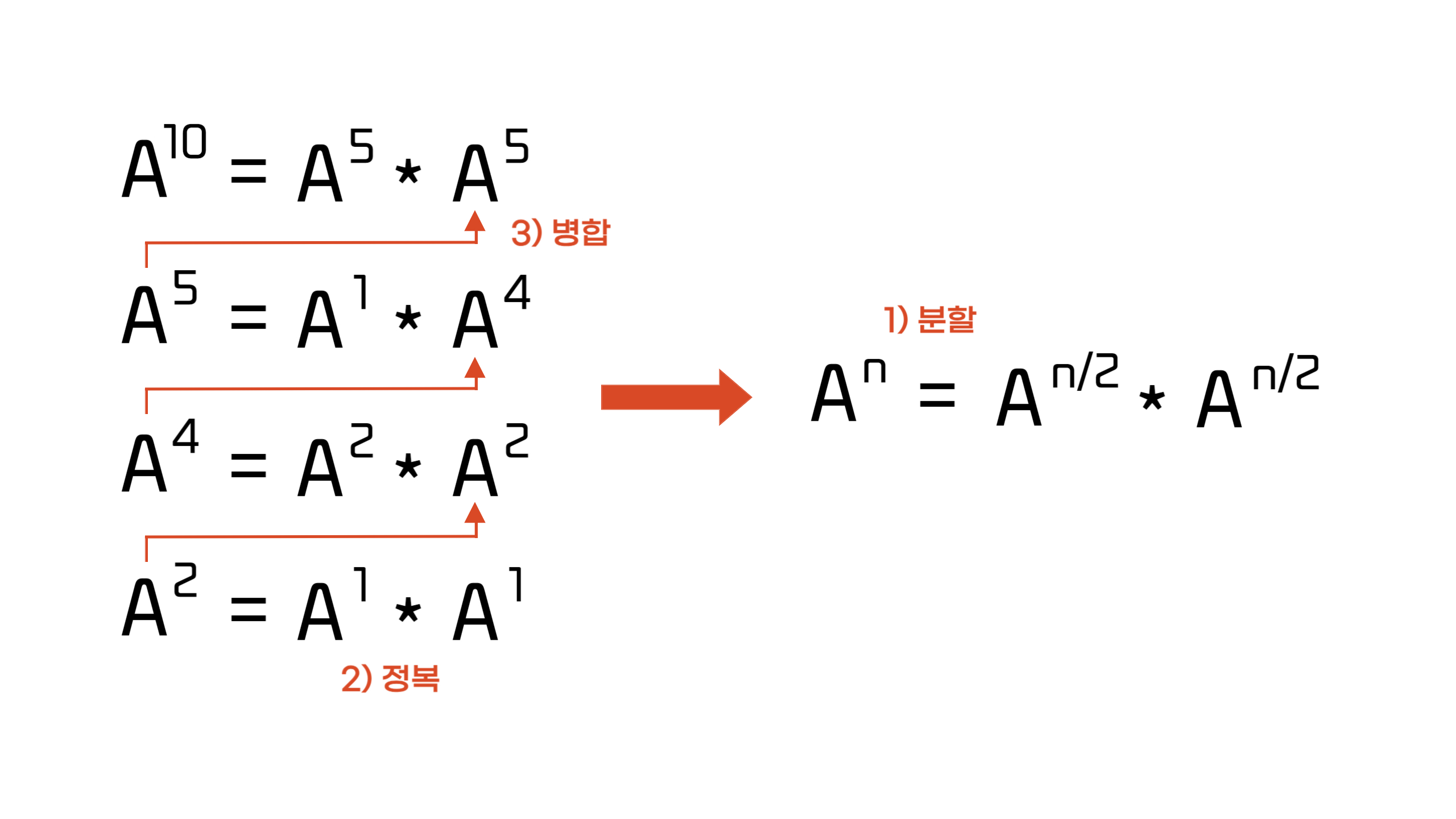
행렬 A의 n제곱의 값을 구한다고 할 때, n이 짝수인 경우는 A^n을 A^(n/2)의 곱으로 나타낼 수 있다. 이러한 수식을 조금 더 구체화 시켜 분할 정복 알고리즘에 적용시켜보자.
- A^n에서 지수 n이 짝수인 경우: A^n = A^(n/2) * A^(n/2)
- A^n에서 지수 n이 홀수인 경우: result *= A
이 때, result의 초기값은 단위 행렬으로 대각성분이 모두 1이고 나머지 값은 모두 0인 행렬로 설정한다. 지수 n이 홀수 일 때 result에 행렬 A를 곱해주는 것은 A^n = A * (A^(n/2))^2 에서 bold체로 표시한 A에 대한 처리이다.
while (power > 0) { //분할정복을 이용한 거듭제곱 계산
if (power % 2 == 1) result = mul(result, mt);
power /= 2;
mt = mul(mt, mt);
}행렬의 곱셈은 mul이라는 함수를 정의하여 사용하였고, 배열은 2차원 벡터를 선언하여 사용하였는데 그냥 이차원 배열을 사용하는 것이 훨씬 간단하였을 듯하다. 또한 using을 이용하여 이차원 벡터에 대한 type alias를 처리해주었다.
드디어 기본적인 자료구조에 대한 내용 복습이 거의 끝나가서 알고리즘 파트로 슬슬 넘어가기 시작했는데, 가장 먼저 보게 된 것이 분할 정복 알고리즘이었다. 작년 학부 알고리즘 시간에 분할 정복의 이론적인 부분은 잘 공부했는데 막상 PS에 사용하려니 어떻게 구조화를 해야될 지 막막했다. 분할 정복 문제를 많이 접해봐야 좀 감이 잡힐 것 같다 😹 쉽지 않다 쉽지 않아 !!
