https://www.bradyneal.com/causal-inference-course
Introduction to Causal Inference라는 강의를 듣고 정리했습니다.

10. Causal Discovery from Observational Data

---

Independence-Based Causal Discovery

casual discovery : data → causal graph
structure identification : causal graph를 identify

10-1. Assumptions

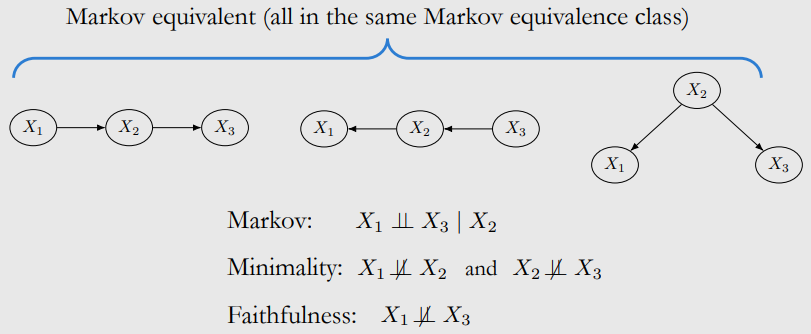
Faithfulness Assumption

• Markov assumption은 causal graph로 data의 distribution을 추론
• faithfulness : data의 independent로 graph 상의 d-seperation을 추론

Violation of Faithfulness

Causal Sufficiency and Acyclicity

• Causal Sufficiency: no unobserved confounders

• Acyclicity: no cycles in the graph

• All assumptions:

  • Markov assumption
  • Faithfulness
  • Causal sufficiency
  • Acyclicity

10-2. Markov Equivalence and Main Theorem

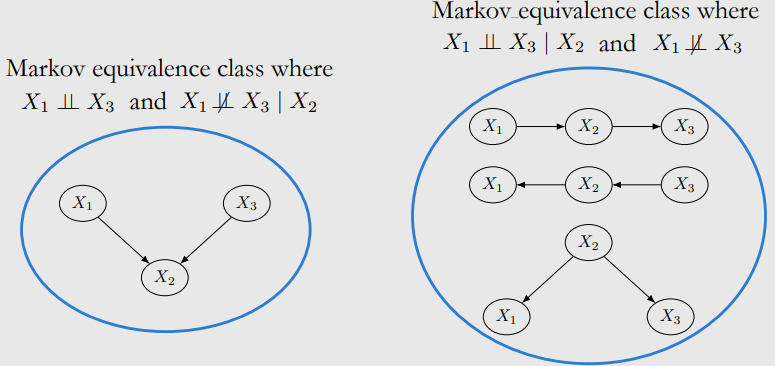
Chains and Forks Encode Same Independencies

• same conditional independency

Immoralities are Special

Skeletons

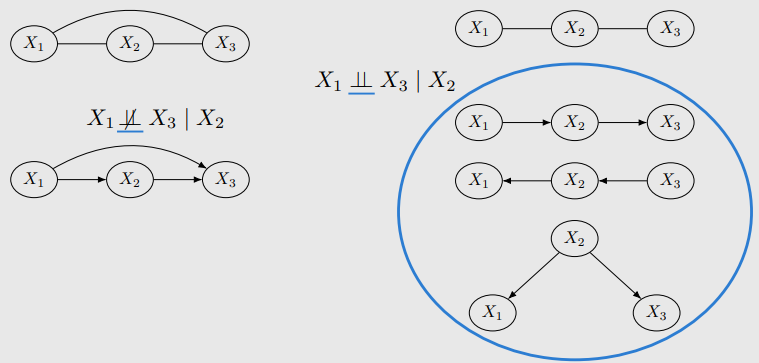
• skeleton으로 markov equivalence class에 대한 정보를 알 수 있다.

Markov Equivalence via Immoral Skeletons

Two important graph qualities that we can use to distinguish graphs:
1. Immoralities
2. Skeleton

Theorem: Two graphs are Markov equivalent if and only if they have the same
skeleton and same immoralities

Essential graph : skeleton + immoralities

• CPDAG : completed partially direct acyclic graph

10-3. The PC Algorithm

PC algorithm

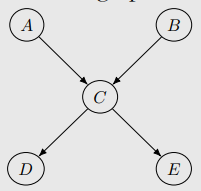
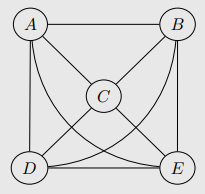
Start with complete undirected graph
Three steps:
1. Identify the skeleton
2. Identify immoralities and orient them
3. Orient qualifying edges that are incident on colliders

Identifying the Skeleton

• undirected graph로 시작
• conditioning set Z(empty도 가능)에 대하여 $X\perp Y | Z$이면 X - Y edge를 삭제
  • empty conditioning set로 시작하여 size를 키움

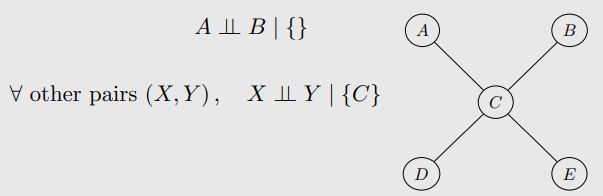
Identifying the Immoralities

X – Z – Y 일 때
1. no edge between X and Y
2. Z 가 X와 Y를 conditionally independent하게 만드는 conditioning set가 아닐 때
(Z를 conditioning 할 때, X랑 Y가 dependent)
X – Z – Y 는 immortality

Orienting Qualifying Edges Incident on Colliders

모든 immoralities를 찾은 상태에서
Z - Y가 X → Z - Y이고, X - Y에 no edge일 때,
Z → Y

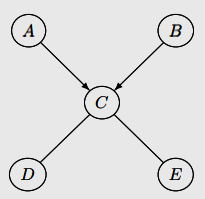
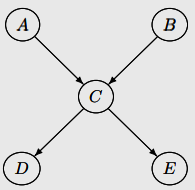
Markov equivalence class를 identify
essential graph에 가끔 undirected edge가 있기도 함

Removing Assumptions

• No assumed causal sufficiency: FCI algorithm
• No assumed acyclicity: CCD algorithm
• Neither causal sufficiency nor acyclicity: SAT-based causal discovery

Hardness of Conditional Independence Testing

• Independence-based causal discovery algorithms은 conditional independence testing으로 함.
• Conditional independence testing은 infinite data면 단순하다.
• finite data면 어렵다.

10-4. Can We Do Better?

• faithfulness로 essential graph를 identify할 수 있다.(Markov equivalence class)
• 더 assumption을 추가해서 narrow down
  • multinomial distributions 이나 linear gaussian structual equations로 markov equivalence class의 graph를 identify할 수 있다.(best)
  • non-gaussian structual equation, nonlinear structural equation은? Semi-parametric causal discovery

Semi-Parametric Causal Discovery

Independence-Based Causal Discovery 문제점

(Semi-Parametric Causal Discovery에는 없는 문제점)

• faithfulness assumption 요구
• conditional independence tests를 위해 large sample 필요
• markov equivalence class만 identify 할 수 있음. → Semi-Parametric Causal Discovery 는 true causal graph 찾을 수 있다

10-5. No Identifiability Without Parametric Assumptions

Two Variable Case: Markov Equivalence

Two Variable Case: SCMs Perspective

뭐가 맞는지 알 수 없다.

parametric form에 대하여 assumption을 만들어야 함

10-6. Linear Non-Gaussian Setting

Linear Non-Gaussian Assumption

• noise가 non-gaussian일 때
  
  

Identifiability in Linear Non-Gaussian Setting

• U가 non-gaussian일 때

• SCM의 reverse direction이 없다.
• Y랑 $\tilde{U}$ dependent

Identifiability in Linear Non-Gaussian Setting: Linear Fit

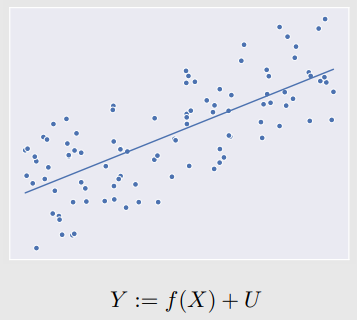
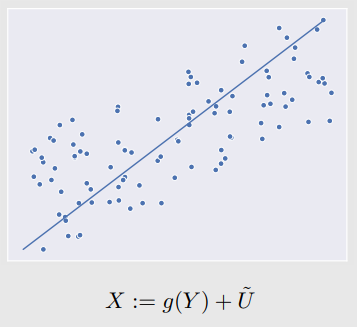
• anti-causal direction을 하면 regression한 것과 결과가 다르다.
• noise term이 non-gaussian이여서 생김.

Identifiability in Linear Non-Gaussian Setting: Residuals

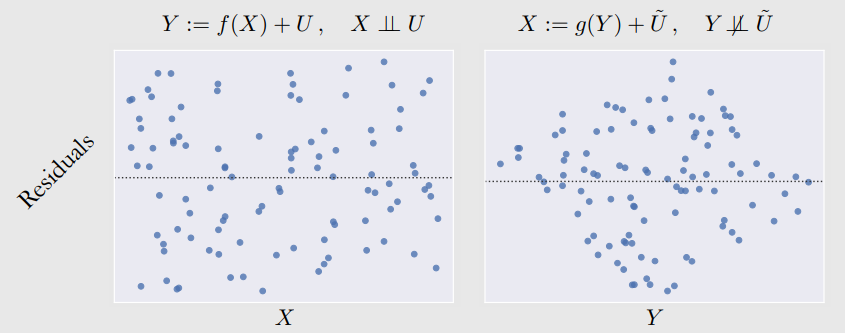
• anti-causal scm을 제대로 구하지 못함. $\tilde{U}$와 Y가 dependent

Linear Non-Gaussian Identifiability Extensions

• Multivariate: Shimizu et al., (2006)
• Drop causal sufficiency assumption: Hoyer et al. (2008)
• Drop acyclicity assumption: Lacerda et al. (2008)

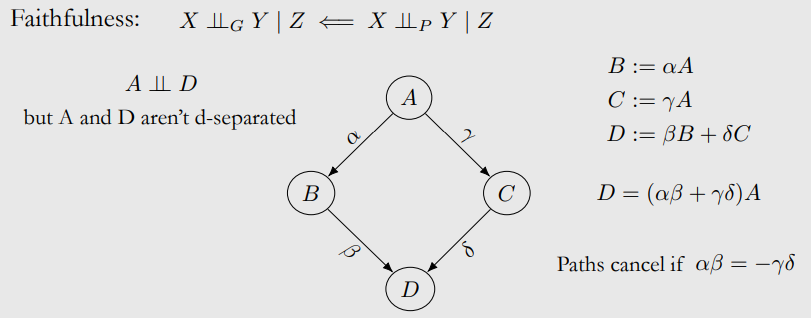
10-7. Nonlinear Additive Noise Setting

Identifiability in Nonlinear Additive Noise Setting

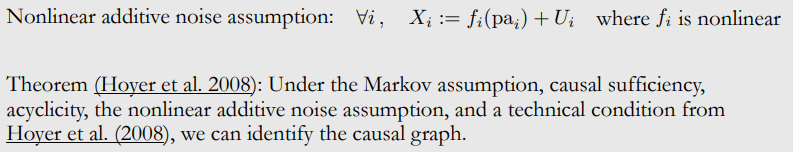
Post-Nonlinear Setting