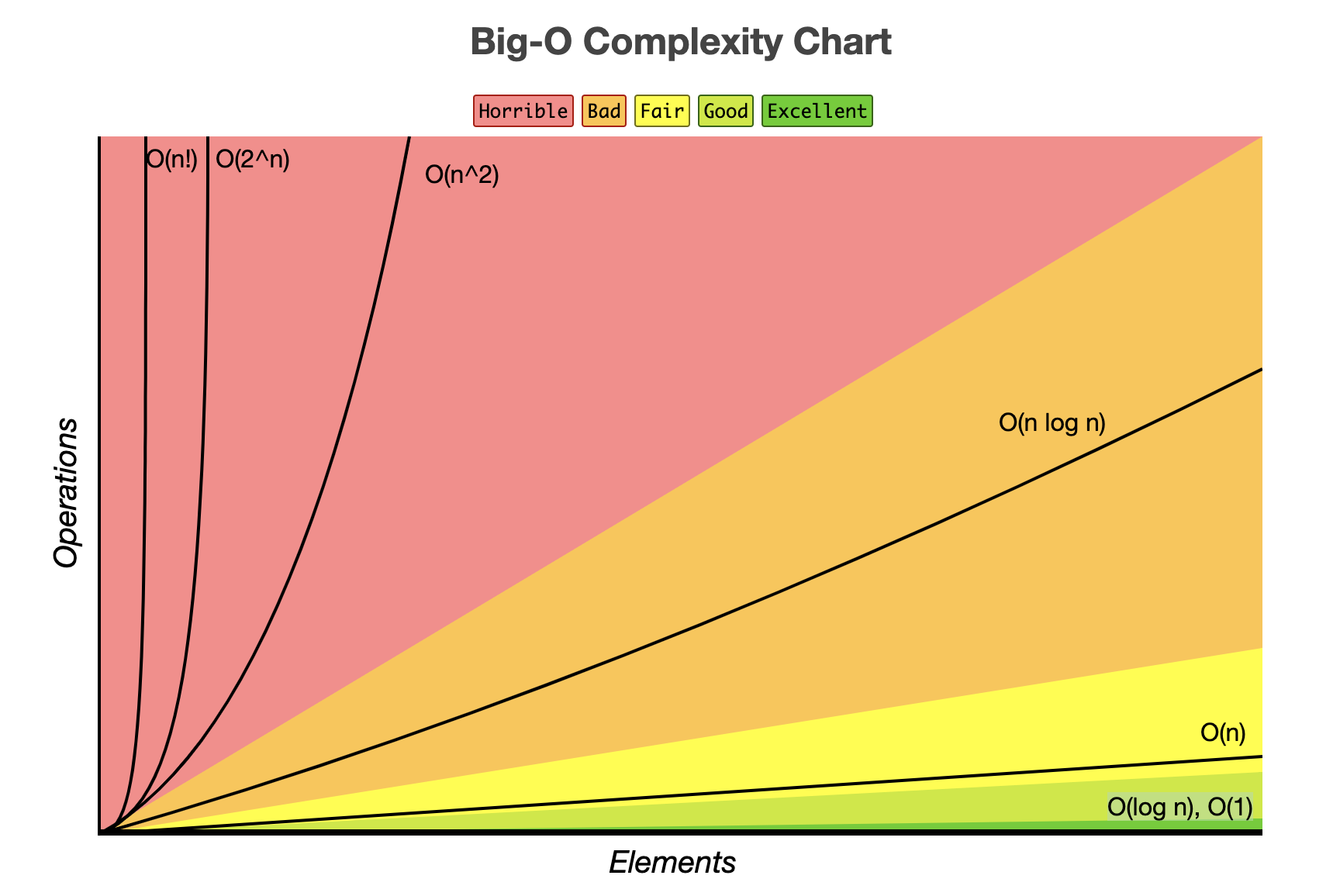
시간 복잡도(Time Complexity)
효율적인 알고리즘을 구현 === 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성
알고리즘의 로직을 코드로 구현할 때, 시간 복잡도를 고려한다는 것 ===
‘입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?’
✨ Big-O 표기법 : 시간 복잡도 표기
입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?
Big-O(빅-오) : 시간복잡도 최악의 경우를 고려
- Big-Ω(빅-오메가) : 최선의 경우
- Big-θ(빅-세타) : 중간(평균)의 경우
✍️ 가장 자주 사용되는 표기법 : Big-O
- 최악의 경우를 고려하므로, 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있다.
- "이 정도 시간까지 걸릴 수 있다"를 고려해야 그에 맞는 대응을 할 수 있다.
| 빅오 표기법 | 1 | 4 | 8 | 32 | 예제 |
|---|---|---|---|---|---|
| O(1) | 1 | 1 | 1 | 1 | 스택의 push,pop |
| O(n) | 1 | 4 | 8 | 32 | for문 |
| O(log n) | 0 | 2 | 3 | 5 | 이진트리 |
| O(n2) | 1 | 16 | 64 | 1,024 | 이중for문, 삽입정렬, 거품정렬, 선택정렬 |
| O(2n) | 2 | 16 | 256 | 4,294,967,296 | 피보나치 수열 |
O(1) : 일정한 복잡도(constant complexity)
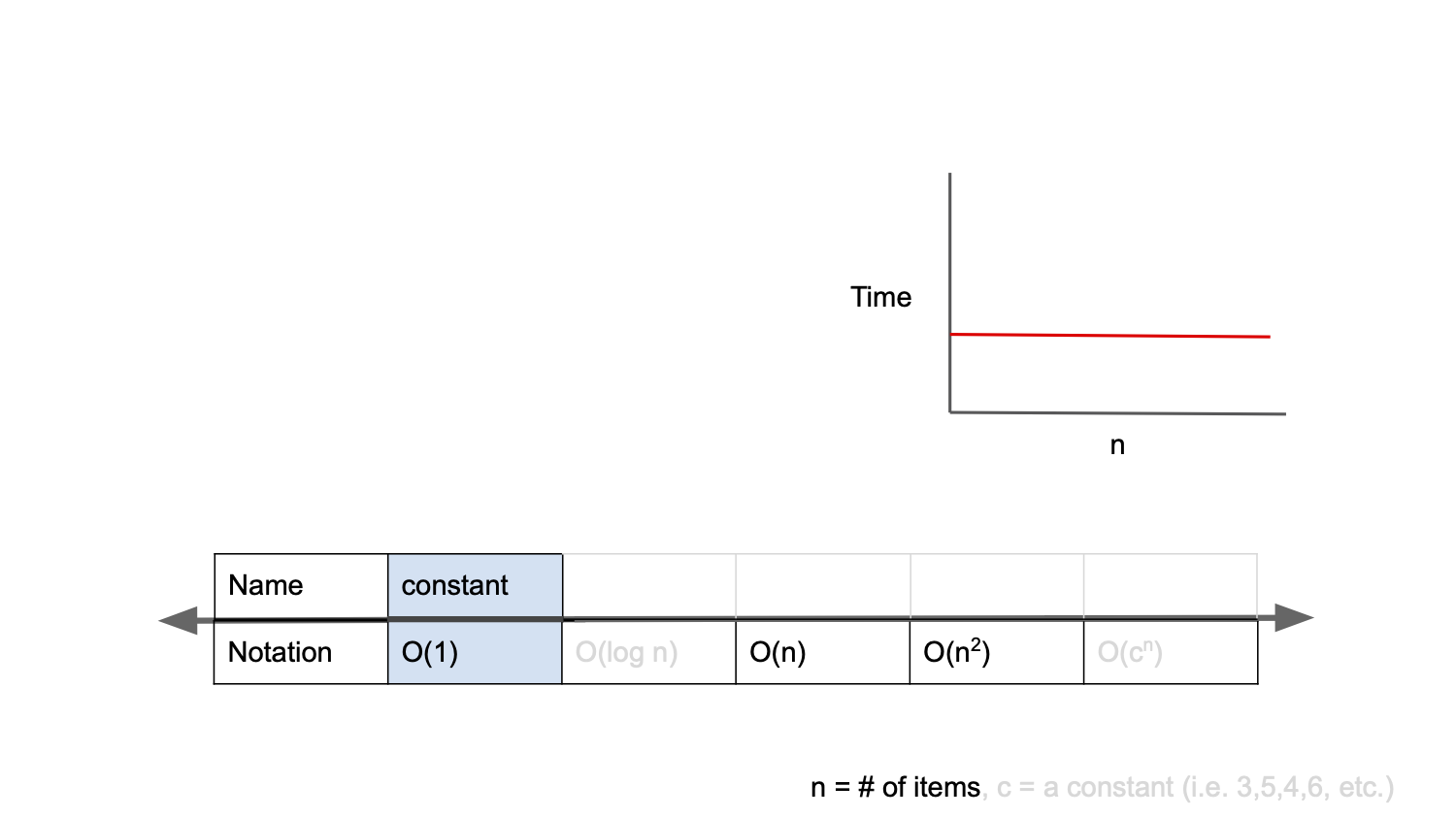
입력값이 증가해도 시간이 늘어나지 않는다.
입력값의 크기와 관계없이 즉시 출력값을 얻어낼 수 있다.
O(n) : 선형 복잡도(linear complexity)
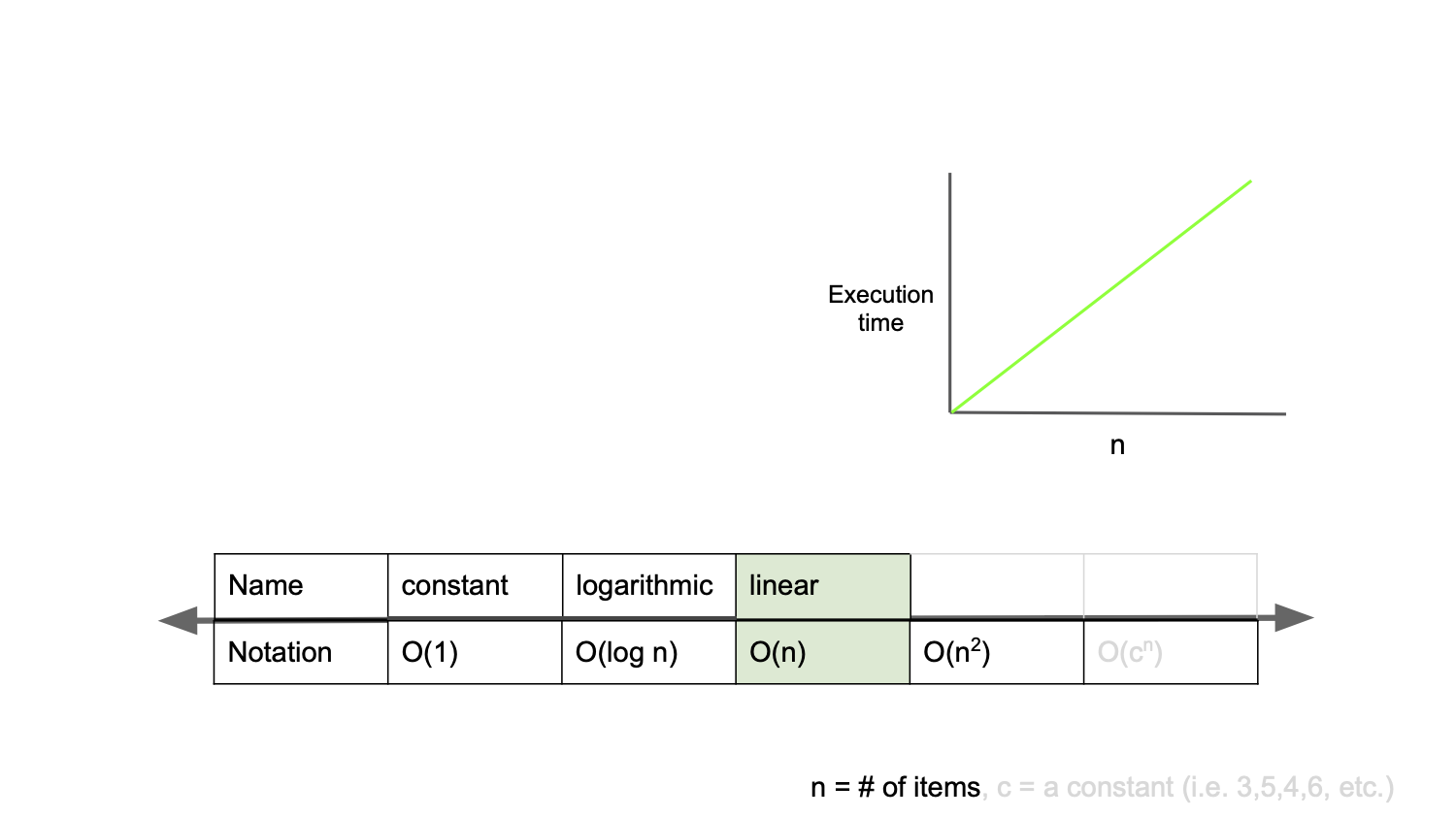
입력값이 증가함에 따라 시간 또한 같은 비율로 증가한다.
ex. 반복문
입력값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때 1초의 100배인 100초가 걸리는 알고리즘을 구현했다면, 그 알고리즘은 O(n)의 시간 복잡도를 가진다고 할 수 있다.
O(log n) : 로그 복잡도(logarithmic complexity)
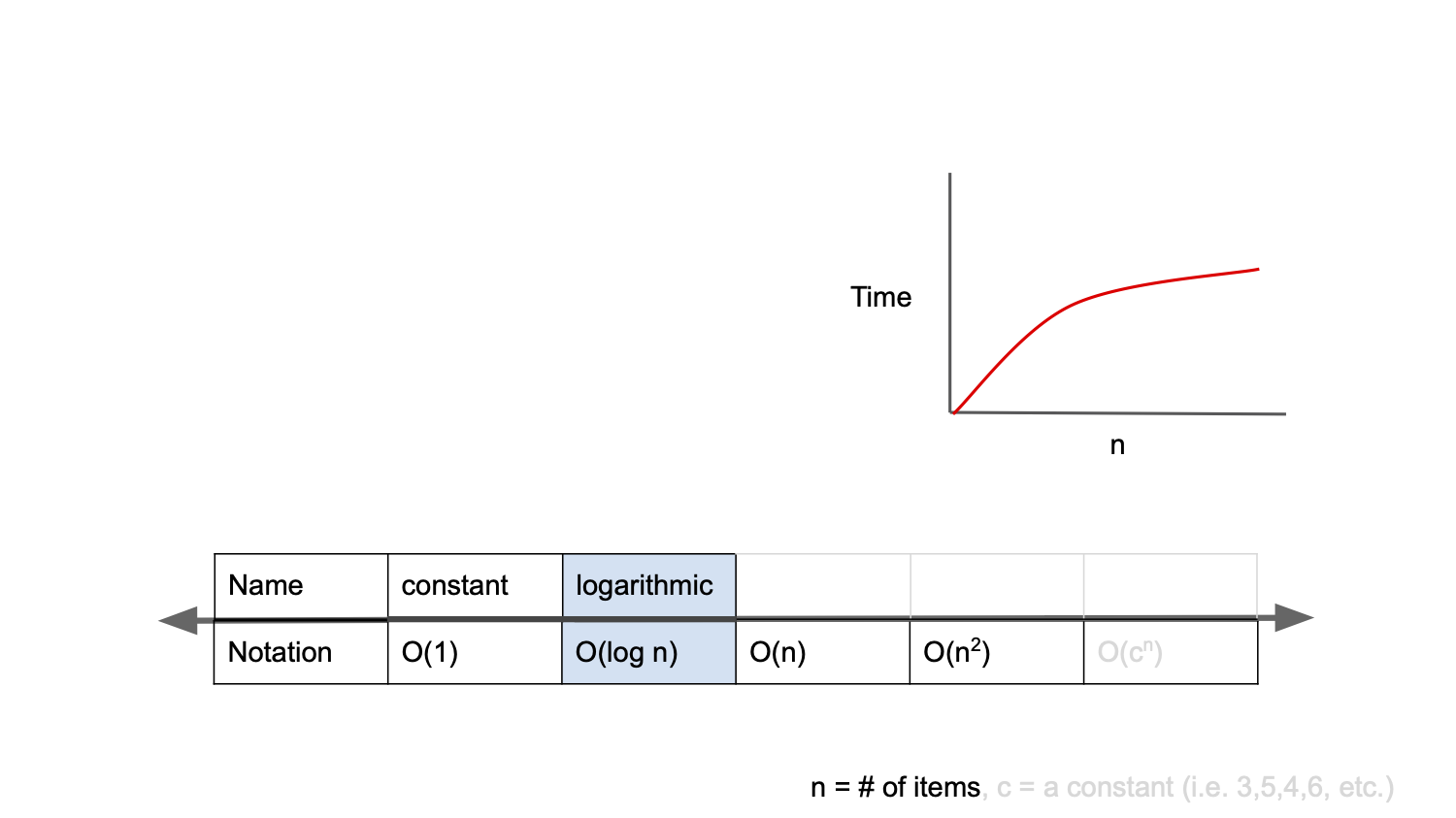
Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다.
ex. BST(Binary Search Tree) : 원하는 값을 탐색할때, 노드를 이동할 때마다 경우의 수가 절반으로 줄어든다.
경우의 수를 계속 절반으로 줄여나가며 정답을 찾는다.
O(n2) : 2차 복잡도(quadratic complexity)
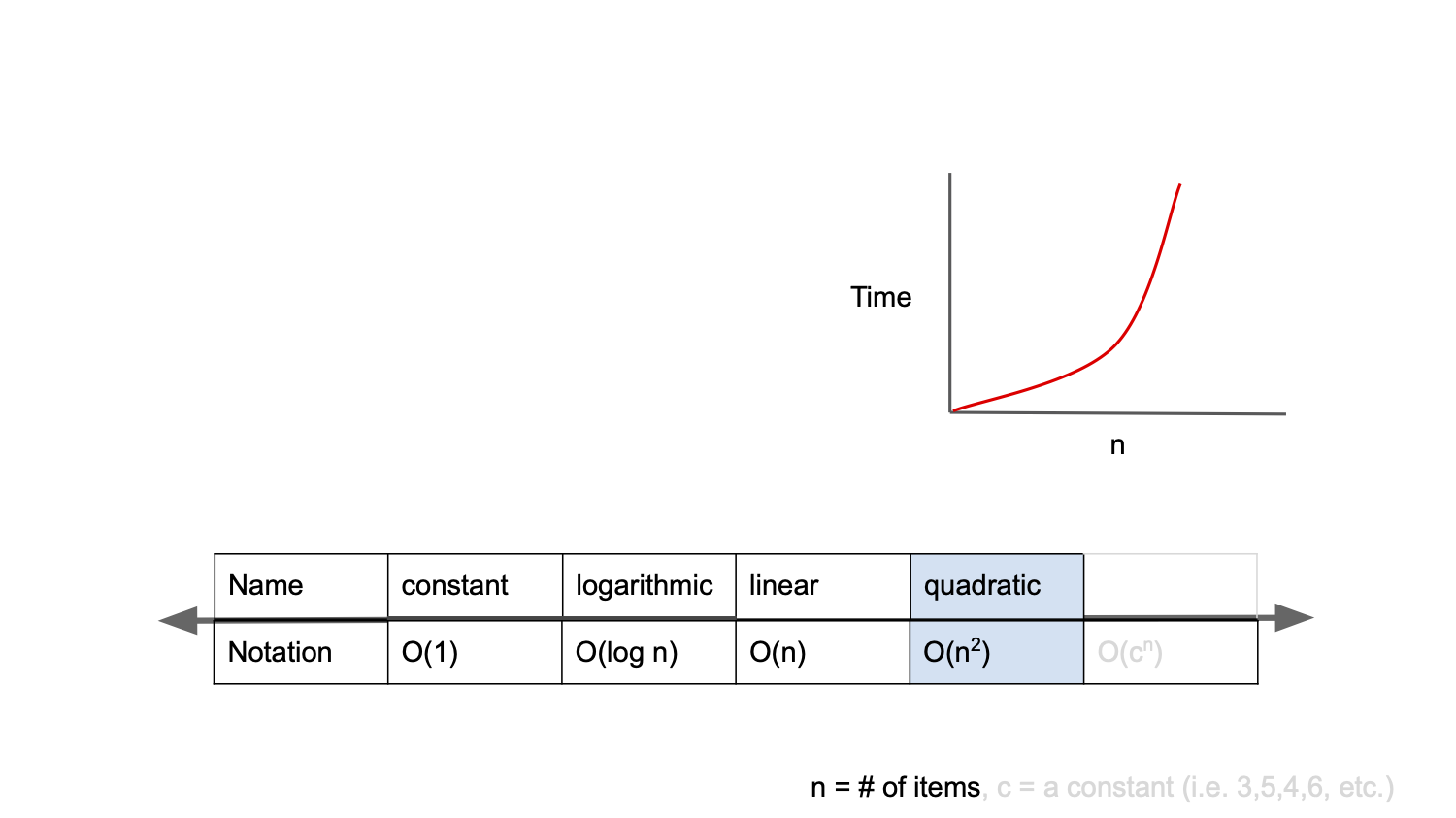
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가한다.
입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 됨
O(n2)의 시간 복잡도를 가진 알고리즘
function O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// do something for 1 second
}
}
}
function another_O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}
// [코드] O(n2)의 시간 복잡도를 가지는 알고리즘 예시- 2n, 5n 을 모두 O(n)이라고 표현하는 것처럼, n3과 n5 도 모두 O(n2)로 표기한다.
- n이 커지면 커질수록 지수가 주는 영향력이 점점 퇴색되기 때문이다.
O(2n) : 기하급수적 복잡도(exponential complexity)
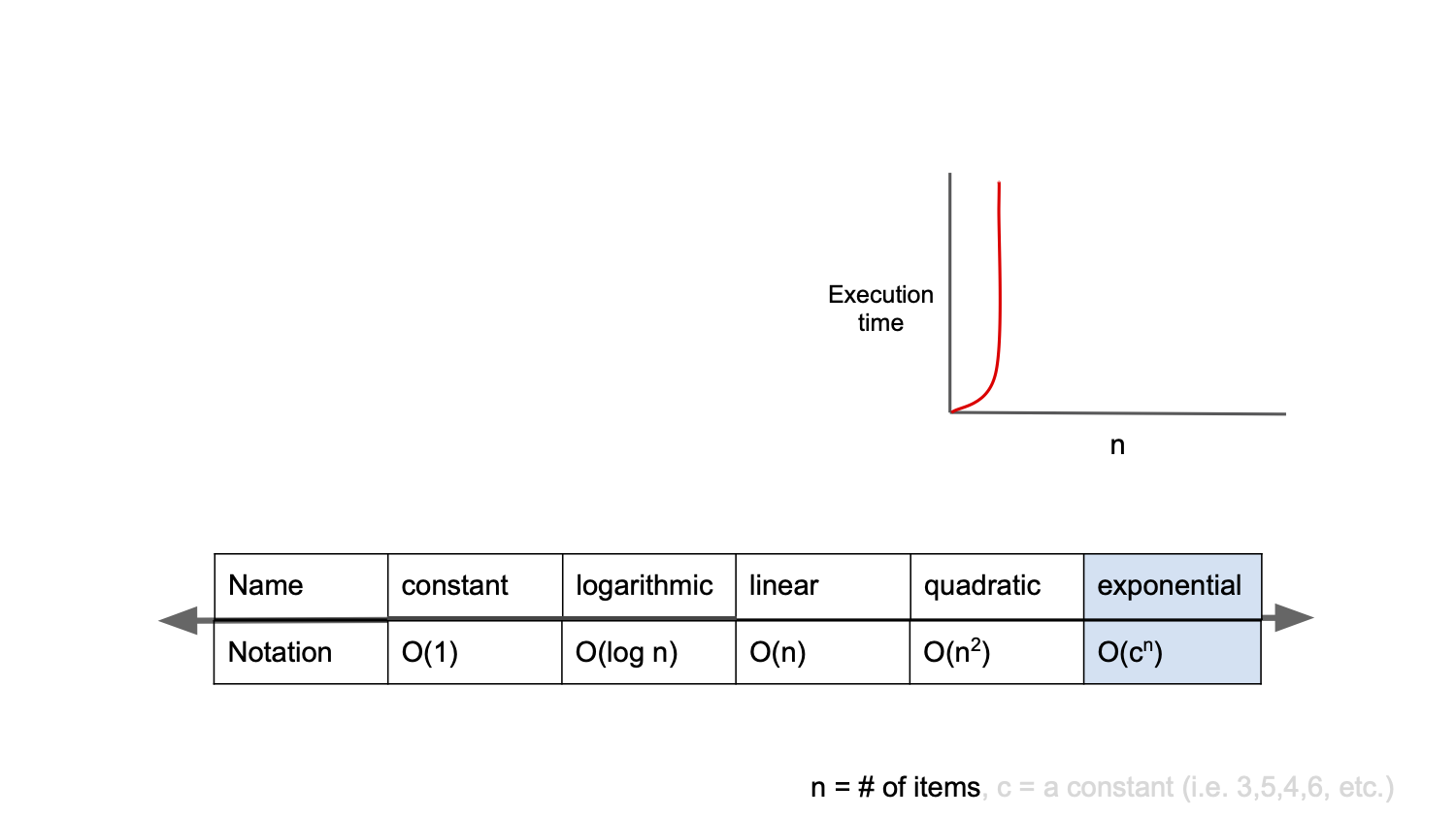
Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.
구현한 알고리즘의 시간 복잡도가 이거라면 다른 접근 방식을 고려하자.
O(2n)의 시간 복잡도를 가진 알고리즘
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
/// O(2n)의 시간 복잡도를 가지는 알고리즘 예시✨ 데이터 크기에 따른 시간 복잡도
n ≤ 500 으로 입력이 제한된 경우 -> O(n³)의 시간 복잡도를 가질 수 있다고 예측할 수 있다. O(n³)의 시간 복잡도를 가지는 프로그램을 작성한다면 문제를 금방 풀 수 있다면, 굳이 시간 복잡도를 줄이려고 할 필요 없다.
즉,
입력 데이터가 클 때 → O(n) & O(log n)의 시간 복잡도를 만족할 수 있도록 예측해서 문제풀기
주어진 데이터가 작을 때 → 시간 복잡도가 크더라도 문제 풀기
| 데이터 크기 제한 | 예상되는시간 복잡도 |
|---|---|
| n ≤ 1,000,000 | O(n) or O (logn) |
| n ≤ 10,000 | O(n2) |
| n ≤ 500 | O(n3) |
공간 복잡도(Space Complexity)
알고리즘이 수행되는 데에 필요한 메모리의 총량,
프로그램이 필요로 하는 메모리 공간 = 고정 공간 요구 + 가변 공간 요구
- 고정 공간 : 처리할 데이터 양에 무관하게 항상 요구되는 공간. 프로그램 성능에 큰 영향 X
- 가변 공간 : 처리할 데이터 양에 따라 다르게 요구되는 공간. 프로그램 성능에 큰 영향 O
공간복잡도도 시간복잡도와 유사하게 빅오 표기법을 사용한다.
✨ 공간 복잡도 예시
function factorial(n) {
if(n > 1) return n * factorial(n - 1);
else return 1;
}n > 1 일 때까지 함수가 재귀적으로 호출되므로 스택에는 n부터 1까지 쌓이게 되므로 공간 복잡도는 O(n)이 된다.
function factorial(n) {
let i = 0;
let fac = 1;
for(i = 1; i <= n; i++) {
fac = fac * i;
}
return fac;
}n의 값과 관계없이 스택에는 n, i, fac 변수만 저장되므로 공간 복잡도는 O(1)이 된다.
✨ 공간 복잡도의 중요성
시간이 적게 소요되는데 메모리가 증가하는 경우는 거의 없음
따라서 시간 복잡도보다 중요성이 떨어짐.
보통 시간 복잡도에 맞다면 공간 복잡도도 통과됨.
공간 복잡도 실패했다면, 보통은 변수 설정 문제
변수 설정할 때 쓸데없는 공간을 많이 차지하도록 설정했을 경우
공간 복잡도 중요한 경우 : 동적 계획법
- 동적 계획법(Dynamic Programming)
- 하나의 큰 문제를 여러 개의 작은 문제로 나눠 그 결과를 저장해 다시 큰 문제를 해결할 때 사용
- 즉, 큰 문제를 작은 문제로 쪼개 그 답을 저장하고 재활용한다.
💡 정리
시간 복잡도 : 얼마나 빠르게 실행되냐
공간 복잡도 : 얼마나 많은 공간이 필요하냐
좋은 알고리즘 : 이 둘을 고려하되, 시간 복잡도 위주로 생각