https://rlakuku-program.tistory.com/39

Greedy Algorithm

그리디 알고리즘은 문제 해결 과정에서 순간순간마다 최적이라고 생각되는 해를 선택하여, 최종 해답에 도달하는 문제 해결 방식이다.

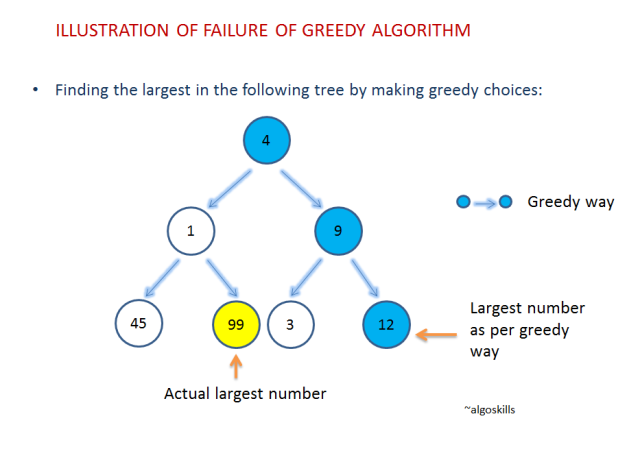
위 그림을 보면, 선택을 해야하는 순간에 가장 최선이라고 생각되는 해를 선택하는 동작방식으로 굴러간다. 최대값을 구해야 한다고 했을 때, 1과 9중 하나를 골라야 할 때, 그 뒤의 값들은 전혀 고려하지 않고, 당장의 1과 9만을 두고 어떤 것을 선택할지 고른다.

1과 9중에는 당연히 9가 크기 때문에 9를 고르고, 3과 12중에는 12를 고르게 된다. 이런식으로 구한 최대값은 12이다. 하지만 그림을 보면 알 수 있듯, 이 이진트리에서 최대값은 99이다.

이렇듯 그리디 알고리즘과 같이 순간순간 최선의 결정을 선택하는 것이 항상 문제의 최선의 해결책이 되지는 않는다.

하지만 이런 단점들을 극복하는 그리디 알고리즘의 가장 큰 장점은 계산 속도에 있다.

그리디 알고리즘을 사용할 수 있는 문제는 아래 두가지 속성을 만족한다.

1. greedy choice property : 앞의 선택이, 이후의 선택에 영향을 주지 않는다.
2. optimal substructure : 문제 전체에 대한 최적해가 부분문제에 대해서도 역시 최적해가 된다.

백준 - 회의실 배정 문제

회사에 회의실이 1개 있다. 각 부서는 미리 회의실 사용을 미리 신청 받아 스케줄링을 한다. 회의실을 사용하고자 하는 부서는 원하는 회의 시작시간과 종료시간을 명시하여 신청서를 제출한다. 이렇게 받은 n개의 회의 신청에 대해 회의실 사용 스케줄을 정하려고 한다.

겹치는 회의가 없게 하면서, 가장 많은 수의 회의를 할 수 있도록 하는 것이 목표이다.

(구현을 위해, 앞 회의 종료 시간과 바로 다음 회의 시작 시간이 같아도 된다.)

생각해 볼 수 있는 Greedy한 아이디어는

1. 소요시간이 가장 짧은 회의순

2. 시작시간이 가장 빠른 회의순

3. 종료시간이 가장 이른 회의순

여러개의 Greedy한 아이디어가 있지만, 이중에서 그리디 알고리즘이 최적해를 보장하는 것은 3. 종료시간이 가장 이른 회의순 뿐이다.

예를 들어, 아래와 같이 8개의 회의가 신청되었다고 하자. (시작 시간, 종료 시간)

(3, 5) , (1, 6) , (6, 7), (5, 9), (8, 13), (7, 14), (12, 18), (16, 20)

위의 알고리즘 대로 회의실 스케줄을 짜면,

(3, 5) , (1, 6) , (6, 7), (5, 9), (8, 13), (7, 14), (12, 18), (16, 20)