그동안 파이썬으로 코딩테스트를 풀면서 heap을 다루는 경우가 종종 있었다.
프로그래머스 야근 지수 문제를 풀면서 힙큐의 사랑스러운 면모를 다시 한 번 깨닫게 되었다.
그래서 힙과 힙큐에 대해 다시 정리해보면서 힙 자료구조 문제들을 다시 한 번 풀어보고자 한다.
1. 힙(Heap)이란?
자료구조를 공부해봤다면 힙이라는 단어는 들어봤을 것이다.
힙은 우선순위 큐를 위해 만들어진 자료구조로, 완전 이진트리의 일종이다.
여러 값 중 최대/최소 값을 빠르게 찾아내도록 만들어진 반정렬 상태이다.
최대/최소 값을 찾기 위해서 O(n)의 시간이 걸리지만, 힙을 사용하면 O(logN) 만큼 소요된다.
힙 트리는 중복된 값을 허용한다는 기특한 특징을 갖고 있다.
우선순위 큐란
들어간 순서와 상관 없이 높은 우선순위를 가진 원소는 낮은 우선순위를 가진 원소보다 먼저 처리
만약 두 원소가 같은 우선순위를 가진다면 큐에서 그들의 순서에 의해 처리
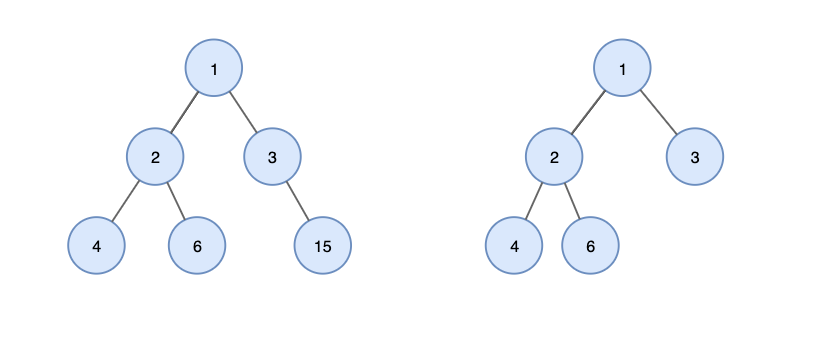
완전 이진트리란
각 노드가 최대 2개의 자식 노드를 갖는 트리 형태
마지막 레벨을 제외한 모든 노드가 완전히 채워짐
최하단 좌측 노드부터 차례로 삽입
왼쪽: 완전 이진트리(X) 오른쪽: 완전 이진트리(O)
1-1. 힙의 종류
최대 힙
부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리이다.
최소 힙
부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리이다.
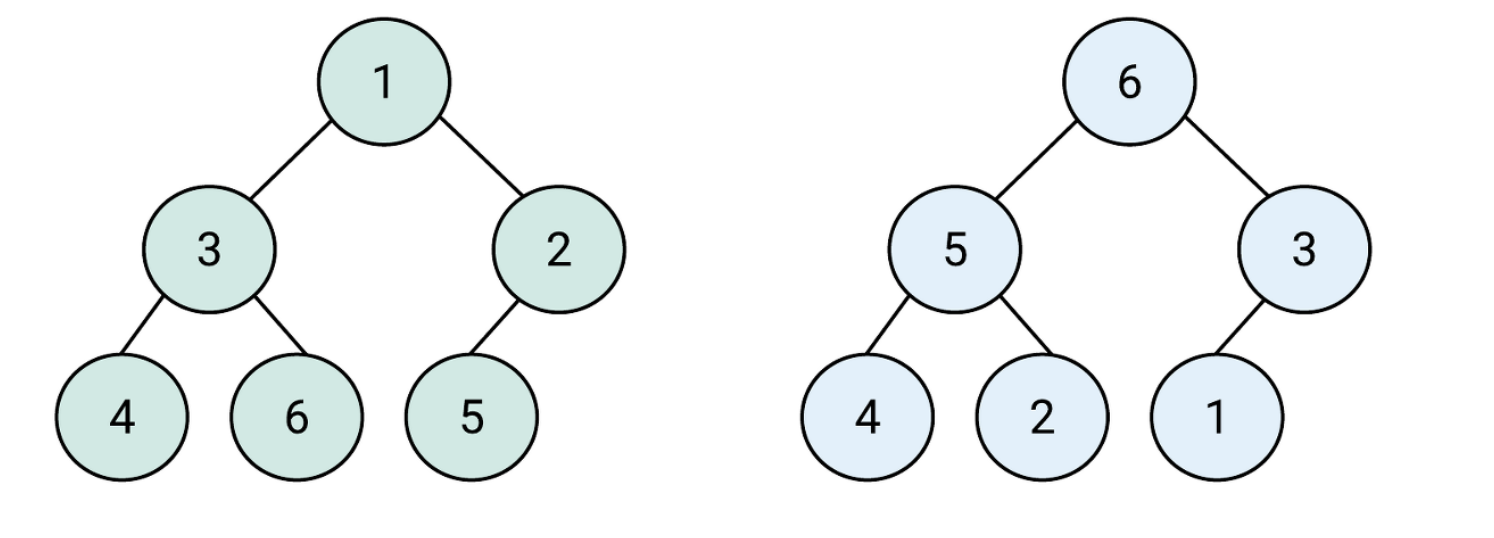
왼쪽: 최소 힙 오른쪽: 최대 힙
2. 힙큐(Heapq)란?
파이썬 내장 모듈인 heapq 는 우선순위 큐 알고리즘인 힙을 제공한다.
내부적으로 최소 힙의 형태로 정렬된다.
2-1. 힙 함수와 힙 동작
heappush(heap, item)
heappush 함수를 통해 item을 heap에 추가한다.
import heapq
heap = []
heapq.heappush(heap, 50)
heapq.heappush(heap, 20)
heapq.heappush(heap, 100)
print(heap) # [20, 50, 100]heapq 모듈을 불러오고 빈 리스트를 생성한다.
리스트를 최소 힙처럼 다룰 수 있도록 하기 때문에 heapq 함수를 호출할 때마다 리스트를 인자에 넘긴다.
item을 추가하면 최소 힙으로 정렬된다.
heappop(heap)
heappop 함수를 통해 heap에서 가장 작은 원소를 제거하고 반환한다.
...
removed_value = heapq.heappop(heap)
print(removed_value) # 20
print(heap) # [50, 100]위에 생성한 리스트에 이어서 가장 작은 요소를 제거해보았다.
가장 작은 원소인 20이 제거되었고 리스트에는 20을 제외한 나머지 값이 남는다.
heapify(list)
heapify 함수를 통해 list를 heap으로 변환한다.
heap2 = [500, 200, 1000]
heapq.heapify(heap2)
print(heap2) # [200, 500, 1000]기존에 있는 리스트를 힙 자료형으로 재정렬하였다.
2-2. 최대 힙 구현
heapq 는 기본적으로 최소 힙만 제공한다.
최대 힙을 구현하기 위해서는 추가적인 절차가 필요하다.
import heapq
values = [1, 2, 3, 4, 5]
heap = []
max_heap = []
for value in values:
heapq.heappush(heap, -value)
print(heap) # [-5, -4, -2, -1, -3]
for i in range(len(heap)):
max_heap.append(-heapq.heappop(heap))
print(max_heap) # [5, 4, 2, 1, 3]리스트의 값을 음수로 바꿔 힙에 추가한다.
가장 작은 값부터 양수로 바꿔 새로운 힙에 추가한다.