
1. 문제


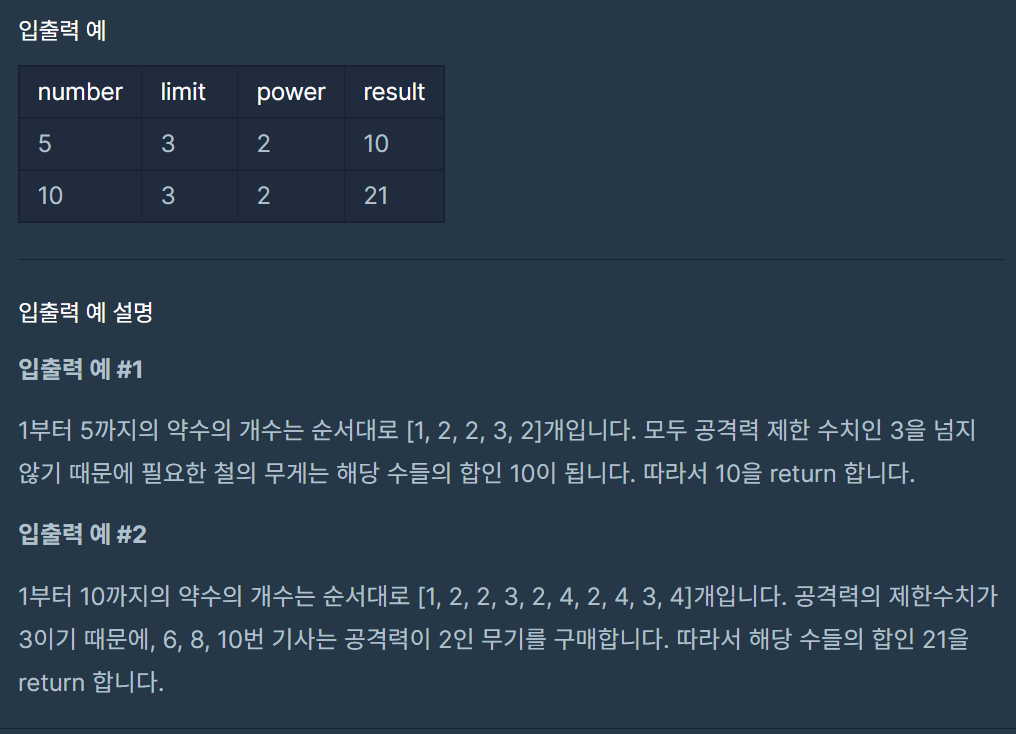
2. 오답
function solution(number, limit, power) {
let answer = 0;
for (let i = 1; i <= number; i++) {
let divisor = 0;
for (let j = 1; j <= i; j++) {
if (i % j == 0) divisor += 1;
if (divisor > limit) {
divisor = power;
break;
}
}
answer += divisor;
}
return answer;
}약수의 합 문제를 풀며 짠 코드를 그대로 가져와 사용해보았다.
function solution(n) {
let sum = 0;
for (let i = 1; i <= n; i++) {
if (n % i == 0) {
sum += i;
}
}
return sum;
}이 코드를 사용할 경우 시간 초과 오류를 가져올 수 있다.
여러 숫자의 약수의 합을 구하는 것이기 때문에 for문을 이중으로 사용할 수 밖에 없고, 결국 시간복잡도는 O(N*N)이 된다.
3. 최종 풀이
function solution(number, limit, power) {
let answer = 0;
for (let i = 1; i <= number; i++) {
let divisor = 0;
for (let j = 1; j <= Math.sqrt(i); j++) {
if (i % j === 0) {
if (i / j === j) divisor += 1;
else divisor += 2;
}
if (divisor > limit) {
divisor = power;
break;
}
}
answer += divisor;
}
return answer;
}시간 초과 문제를 해결하기 위하여 Math.sqrt()를 사용하였다.
이 방식을 사용하면 다음과 같이 약수의 개수를 구할 수 있다.
i가 4인 경우
j가 1인 경우
4 % 1 === 0이므로 계속 진행
4 / 1 === 4이므로 약수의 개수는 +2
j가 2인 경우
4 % 2 === 0이므로 계속 진행
4 / 2 === 2이므로 약수의 개수는 +1약수의 개수 : 3개
i가 10인 경우
j가 1인 경우
10 % 1 === 0이므로 계속 진행
10 / 1 === 10이므로 약수의 개수는 +2
j가 2인 경우
10 % 2 === 0이므로 계속 진행
10 / 2 === 5이므로 약수의 개수는 +2
j가 3인 경우
10 % 3 === 1이므로 건너 뛰기약수의 개수 : 4개
시간복잡도 O(N*√ N)가 되므로 시간초과 에러를 피할 수 있다.
참고 링크 : https://www.geeksforgeeks.org/count-divisors-n-on13/
