WEEK04

yeopto·2022년 5월 1일

CSAPP SW사관학교 정글 algorithm python sw정글

SW사관학교 정글

목록 보기

6/14

22.04.21 ~ 22

알고리즘

시간복잡도(Big O)
- 완료까지 걸리는 절차로 결정 됨
- 선형검색은 알고리즘 한 개씩 검사해보는 것이므로 N개의 input이 있다면 N번의 수행을 해야하므로 O(N)이다.
```
Array = ["kimchi1", "pizza2",..., "galbi100"]

def print_first(arr):
		print(arr[0])
```
- 위 경우 input이 100개라도 한번만 실행하는 코드이다. input이 몇개라도 이 함수는 동일한 스텝이 필요하다. 이 함수의 시간복잡도는 constant time(상수 시간) O(1) 라고 표현할 수 있다.
- 이중 반복문은 O(n^2) → n번만큼 n번 수행하니까.
- 로그와 지수는 반대개념이다. 이진탐색은 매번 반으로 나누면서 수행하니까 O(logn)이다. input이 두배가 되도 단계는 한번만 더 나눠주면 됨.

그리디 알고리즘

현재 상황에서 지금 당장 좋은 것만 고르는 방법
그리디 해법은 그 정당성 분석이 중요하다.
- 단순히 가장 좋아 보이는 것을 반복적으로 선택해도 최적의 해를 구할 수 있는지 검토한다.
일반적인 상황에서 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많다.
문제 - 1이 될 때까지

n, k = map(int, input().split())

result = 0

while True:
		target = (n // k) * k # k로 나누어 떨어지는 수 중 가장 가까운 수를 찾기위해
		result += (n - target) # 1씩 빼는건 몇번 수행해야하는지 알기위함
		n = target
		
		if n < k:
				break
		result += 1
		n //= k

# n이 1보다 클 때 마지막으로 남은 수에 대해 1씩 빼기
result += (n - 1)
print(result)

동적 프로그래밍(다이나믹 프로그래밍)
- 다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법
- 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다.
- 다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식(top-down, bottom-up)으로 구성된다.
- 일반적인 프로그래밍에서 동적(Dynamic)이란?
  - 자료구조에서 동적 할당은 ‘프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법'을 의미
- 다이나믹 프로그래밍은 문제가 다음 조건을 만족할 때 사용할 수 있다.
  - 최적 부분 구조 (Optimal Substructure)
    - 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
  - 중복되는 부분 문제 (Overlapping Subproblem)
    - 동일한 작은 문제를 반복적으로 해결해야 한다.
- 피보나치 수열
  - 피보나치 수열은 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... 으로 나열된다.
  - 점화식이란 인접한 항들 사이의 관계식을 의미.
  - 피보나치 수열 점화식
  - 프로그래밍에서는 이러한 수열을 배열이나 리스트를 이용해 표현한다.
  - 단순 재귀 함수로 피보나치 수열을 해결하면 지수 시간 복잡도를 가지게 된다.
  - f(6)을 호출하면 f(2)가 다섯번이나 호출 됨.(중복되는 부분 문제)
  - 피보나치 수열은 다이나믹 프로그래밍의 사용 조건을 만족한다.(큰 문제를 작은 문제로 나눌 수 있음)

22.04.23

알고리즘

메모이제이션 (Memoization) → 하향식(top-down)
- 한 번 계산한 결과를 메모리 공간에 메모하는 기법
  - 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져온다.
  - 별도의 테이블 즉 배열에 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 한다.
top-down vs bottom-up
- 다이나믹 프로그래밍의 전형적인 형태는 상향식(bottom-up) 방식이다.
  - 결과 저장용 리스트는 DP테이블이라고 부른다.
- 엄밀히 말하면 메모이제이션은 이전에 계산된 결과를 일시적으로 기록해 놓은 넓은 개념을 의미
  - 메모이제이션은 다이나믹 프로그래밍에 국한된 개념이 아니다.
  - 한번 계산된 결과를 담아 놓기만 하고 다이나믹 프로그래밍을 위해 활용하지 않을 수도 있다.

탑다운 형식의 피보나치 수열 → O(N)

d = [0] * 100 # 메모이제이션을 하기 위한 리스트 초기화

def fibo(x):
		if x == 1 or x == 2:
				return 1
		if d[x] != 0: # 이미 계산한 적 있는 문제라면 그대로 반환
				return d[x]
		d[x] = fibo(x - 1) + fibo(x - 2)
		return d[x]

print(fibo(99))

바텀업 형식의 피보나치 수열

d = [0] * 100

d[1] = 1
d[2] = 1
n = 99

for i in range(3, n + 1):
		d[i] = d[i - 1] + d[i - 2]

print(d[n])

Computer System(CSAPP)

3.2 프로그램의 인코딩
- gcc -Og -o p p1.c p2.c
  - 커맨드 라인 옵션 -Og 를 주면 컴파일러는 본래 C 코드의 전체 구조를 따르는 기계어 코드를 생성하는 최적화 수준을 적용한다. → 최적화 수준을 올리게 되면 최종 프로그램은 더 빨리 동작하게 되지만, 컴파일 시간이 증가하고, 디버깅 도구를 실행하기 어려워질 위험이 있다. 높은 수준의 최적화를 적용하면 만들어진 코드가 너무 많이 변경되어서 본래의 코드와 생성된 기계어 코드 간의 관계를 이해하기가 어렵다. 실제로는 더 높은 단계의 최적화가 프로그램 성능적인 면에서 더 좋은 선택임.
- gcc -Og -S mstore.c
  - 어셈블리 코드를 보기 위해 -S 옵션을 사용할 수 있다.
- gcc -Og -c mstore.c
  - 직접 볼 수 없는 목적코드 파일 mstore.o를 생성함.
- objdump -d mstore.o
  - 기계어 코드 파일의 내용을 조사를 한다. 역어셈블러

22.04.24

Computer System(CSAPP)

3.3 데이터의 형식
- 포인터들은 8byte로 쿼드워드로 저장됨.
- 데이터 이동 인스트럭션에는 네 개의 유형이 존재한다.
  - movb : 바이트이동
  - movw : 워드 이동
  - movl : 더블워드 이동
  - movq : 쿼드워드 이동
- 주의 - 어셈블리 코드가 접미어 ‘l’을 4바이트 정수뿐만 아니라 8바이트 더블 정밀도 부동소수점 수를 나타내기 위해서도 사용한다! → 사실 혼란을 야기하진 않음 부동소수점 경우 완전히 다른 인스트럭션과 레지스터들을 사용하기 때문.
3.4 정보 접근하기
- x86-64 주처리장치 CPU는 64비트 값을 저장할 수 있는 16개의 범용 레지스터를 보유하고 있음
- 이들 레지스터는 정수 데이터와 포인터를 저장하는 데 사용한다.

22.04.25

알고리즘

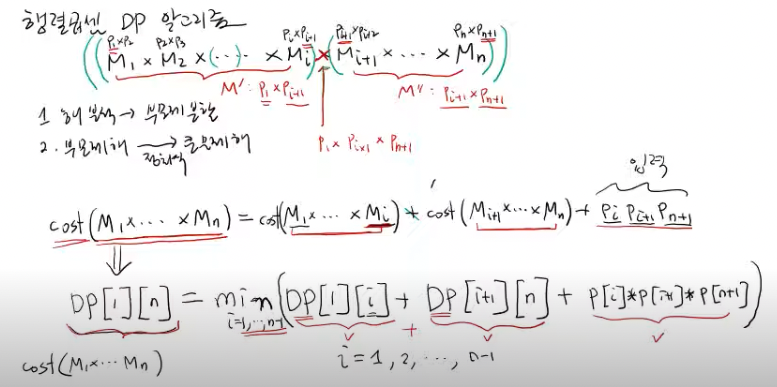
행렬 곱셈 순서(BOJ 11049)
- 연쇄 행렬 곱셈 문제의 이해
  - 2 X 3 행렬과 3 X 4 행렬을 곱하면 2 X 4 행렬이 나옴
  - 원소를 곱하는 횟수는 2 3 4 = 24
  - 일반적으로 i k 행렬과 k j 행렬을 곱하면 i * j 행렬이 나옴
    - 원소 곱셈 횟수 → i k j
  - 브루트포스(카탈란 넘버수)로 접근하면 시간이 너무 오래걸림

Computer System(CSAPP)

movq는 Source에 해당하는 값은 Dest가 나타내는 공간에 이동시킨다.
상수(Immediate)는 Dest자리에 올 수 없다.
메모리와 메모리 사이의 데이터 이동은 불가하다. → 이를 위해서는 메모리에서 값을 읽어와서 레지스터에 저장한 뒤, 그것을 다시 메모리에 적도록 해야함.

leaq 이는 메모리에 직접 접근하지 않고 특정 메모리 주소를 계산해 내는 명령어이다. 메모리에 접근하지 않고 원하는 메모리 주소를 계산해낸다.

22.04.26

Computer System(CSAPP)

x86-64에서 현재 실행 중인 프로그램에 대한 정보들에는 여러 임시 데이터들을 저장하는 %rax와 같은 범용 레지스터들과, 현재 런타임 스택의 스택포인터를 저장하는 %rsp 레지스터가 있다. 그리고 다음 실행할 명령의 메모리 주소를 저장함으로써 현재의 제어 위치를 나타내는 %rip 레지스터가 있다. 또한 조건 분기/이동에 사용되는 상태 값을 저장하는 컨디션 코드 레지스터들도 있다.

컨디션 코드(Condition Code)
- x86-64의 컨디션 코드 레지스터는 총 4개
  - CF : 연산 시 최상위비트로부터 올림이 발생하거나 내림이 발생하면 세팅된다 (unsigned 연산에만 의미 있음) → 부호없는 값의 Carry Out 발생 여부를 나타냄
  - ZF : 연산 결과값이 0이면 세팅됨 → 값이 0인지 나타냄
  - OF : 연산 시 오버플로우가 발생하면 세팅됨 (signed 연산에서만 의미 있음)
  - SF : 연산 결과값의 최상위비트가 1이면 세팅됨 → 부호 있는 값의 부호를 나타냄
- 값에 대한 특정 연산을 수행하는 계산 명령어가 실행되고 나면, 그 결과값에 의해 컨디션 코드 레지스터들의 값이 자동으로 세팅된다. → 암묵적 방법
  - ex) “addq A,B” 명령어를 실행하여 (A + B)를 계산을 함
    - CF : 덧셈 시 최상위비트로 Carry out이 발생하면 세팅됨
    - ZF : (A + B == 0)이면 세팅됨
    - SF : (A + B)의 최상위 비트가 1이면 세팅됨
    - OF : (A > 0 && B > 0 && (A + B) < 0) 또는 (A < 0 && B < 0 && (A + B) ≥ 0)이면 세팅됨 → 저 식은 https://modoocode.com/308 에서 참고하여 이해함.
    - 참고할점은 CF는 부호 없는 값의 덧셈 시에 오버플로우를 감지하는 수단이 되고, OF는 부호 있는 값의 덧셈 시에 오버플로우를 감지하는 수단이 됨. (signed가 오버플로우가 되면 -2147483648, unsigned는 0이 됨)
- 컨디션 코드 레지스터들의 값을 직접 조작하기 위한 명령어들도 따로 존재함 → 명시적 방법
  - Compare 명령어
    - cmpq B, A → (A - B)의 결과에 따라 컨디션 코드 레지스터들의 값을 세팅
      - CF : 뺄셈 시 최상위비트에서 Borrow가 발생한 경우 세팅됨. (부호 없는 값의 비교에서 사용됨)
      - ZF : (A - B == 0)이면 세팅됨
      - SF : (A - B)의 최상위비트가 1이면 세팅됨 (부호 있는 값의 비교에서 사용됨)
      - OF : (A > 0 && B < 0 && (A - B) < 0)이거나 (A < 0 && B > 0 && (A - B) ≥ 0)이면 세팅됨
  - Test 명령어
    - testq B, A → (A & B)의 결과에 따라 컨디션 코드 레지스터들의 값을 세팅
      - ZF : (A & B == 0)이면 세팅됨
      - SF : (A & B)의 최상위비트가 1이면 세팅됨
- movzbl, movsbl
  - movzbl A, B → A를 Zero Extenstion 한 결과를 B에 넣는다 (32비트 명령어)
  - mobsbl A, B → A를 Sign Extenstion 한 결과를 B에 넣는다 (32비트 명령어)
x86-64 스택
- 스택은 stack discipline에 의해 관리되는 메모리 영역을 말한다. stack discipline이란 스택을 관리하기 위한 일종의 규율과 같은 것
- x86-64에서는 %rsp 레지스터가 현재 스택의 가장 낮은 주소를 저장하기로 되어있다. 스택에 데이터가 쌓일 때는 낮은 주소 방향으로 쌓이도록 약속이 되어있다. 데이터를 push 할때는 %rsp의 값을 8만큼 감소시켜야한다. pop할 때는 %rsp의 값을 8만큼 증가시켜야 할 것이다.

22.04.27

Computer System(CSAPP)

callq LABEL → 함수 호출 : 1. 복귀 주소를 현재 스택 프레임에(Push), 2. LABEL 주소로 점프
ret → 함수 리턴 : 1. 스택에 저장된 복귀 주소를 팝(Pop), 2. 복귀 주소로 점프

데이터 전달
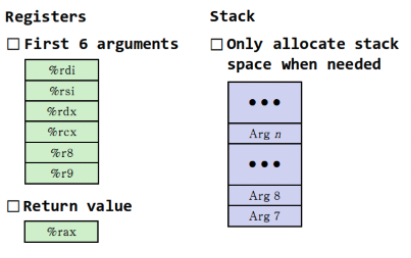
- 함수의 1번째 ~ 6번째 인자는 %rdi, %rsi, %rdx, %rcs, %r8, %r9 레지스터에 차례로 저장이 된다.
- 그리고 7번째 ~ n번째 인자는 Caller의 스택 프레임에 역순서로 푸시된다.
- Caller는 call 명령어를 통해 또 다른 함수를 호출하기 전에 반드시 인자들을 적절한 레지스터 혹은 스택 공간에 넣어주는 작업부터 선행해야 한다. 따라서 인자가 6개보다 많으면 복귀 주소보다 인자가 먼저 스택에 쌓이게 됨.
스택 프레임
- 함수 하나가 호출될 때마다 스택 프레임(Stack Frame) 하나가 스택에 푸시되어 그곳에서 그 함수의 지역 데이터들이 관리되며, 함수가 리턴할 때 해당 스택 프레임이 스택에서 팝이 된다.
- 함수를 호출할 때 실행하는 call 명령어에 의해서 복귀 주소가 Caller 스택 프레임에 푸시되고, 호출된 함수 내에서 초반부에 실행되는 "Set-up" 코드에 의해 해당 함수 내에서 필요로 하는 지역 데이터들이 할당된다.
- 호출된 함수 내에서 리턴하기 직전에 실행되는 "Finish" 코드에 의해 현재 스택 프레임에 저장되어 있는 지역 데이터들이 팝이 되고, 리턴할 때 실행하는 ret 명령어에 의해 Caller 스택 프레임에 잔존해 있던 복귀 주소도 팝을 하게 된다.
레지스터의 백업 및 복원
- x86-64의 레지스터는 크게 두 종류로 나뉜다. 바로 Caller-save 레지스터와 Callee-save 레지스터이다.
- Caller-save 레지스터
  - Caller-save 레지스터는 마음껏 건드려도 괜찮은 레지스터로, 새로 호출할 함수가 그 값을 변경시켜도 할 말이 없음. 따라서 새로 호출할 함수에 의해 값이 손실되면 안 되는 경우에는, Caller가 직접 자신의 스택 프레임에 그 값을 백업하고, 나중에 해당 함수가 리턴한 직후에 다시 복원을 해야 한다.
- Callee-save 레지스터
  - Callee-save 레지스터는 함부로 건드리면 안 되는 레지스터로, 새로 함수가 호출되더라도 Caller에게 리턴했을 때 그 값이 변경되어 있으면 안 된다. 따라서 자신이 Callee-save 레지스터를 건드려야 하는 상황이라면 그전에 먼저 그 값을 자신의 스택 프레임에 백업하고, 나중에 리턴하기 직전에 다시 복원을 해야 한다.
- 위 기준으로 나눈 x86-64 레지스터
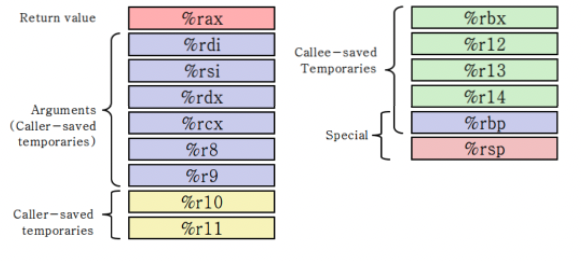
  - %rax : 반환 값이 저장되는 레지스터이다. Callee에 의해 변경될 수 있으므로 Caller-save 레지스터이다.
  - %rdi ~ %r9 : 함수의 인자가 저장되는 레지스터이다. Callee에 의해 변경될 수 있으므로 Caller-save 레지스터이다.
  - %r10, %r11 : 마음껏 건드려도 괜찮은 Caller-save 레지스터이다.
  - %rbx, %r12 ~ %r14 : 함부로 건드리면 안 되는 Callee-save 레지스터이다.
  - %rbp : 스택 프레임의 Frame Pointer로 사용되는 레지스터로, 함부로 건드리면 안 되는 Callee-save 레지스터이다.
  - %rsp : Callee-save 레지스터의 특별한 경우로, 함수 리턴 직전 "Finish" 코드에 의해 원래 값으로 복원이 된다.
재귀 함수의 구현
- C 언어와 같은 스택 기반 언어는 재진입성을 갖추고 있다. 즉 한 프로시저에 대해 여러 개의 인스턴스가 만들어질 수 있으며, 각 인스턴스는 자신만의 지역 데이터를 관리하기 위한 스택 프레임을 가지고 있다는 것이다. 또, 스택은 함수의 호출 및 리턴 패턴(나중에 호출된 것이 먼저 리턴)을 LIFO(Last-In First-Out) 구조로서 지원하고 있다. 이러한 측면에서 봤을 때, 재귀 함수를 구현하는 것은 별도의 작업이 전혀 필요하지 않다. 단순히 또 다른 함수를 호출하는 것과 같은 메커니즘으로 처리하면 된다.
배열
- T A[L]
  - 자료형이 T인 데이터 L개로 이뤄진 배열 A를 선언하는 문장
  - 배열의 할당은 어셈블리어 수준에서 메모리에 L x sizeof(T) 바이트를 연속적으로 할당함으로써 구현된다. 그리고 배열 요서의 접근은 어셈블리어 수준에서 배열의 첫 번째 요소를 가리키는 포인터인 A에 특정 인덱스 값을 더한 주소에 접근하는 방식으로 구현됨. A는 배열의 첫 번째 요소를 가리키는 자료형이 T* 포인터다.
멀티-레벨 배열
- 멀티-레벨 배열은 각 요소가 특정 배열을 가리키는 포인터인 배열을 의미함
- 다차원 배열과의 차이점은 크게 두 가지이다. 첫 번째 차이점은 각 요소에 해당하는 배열들이 메모리 상에서 순차적으로 할당된다는 보장이 없다는 것.
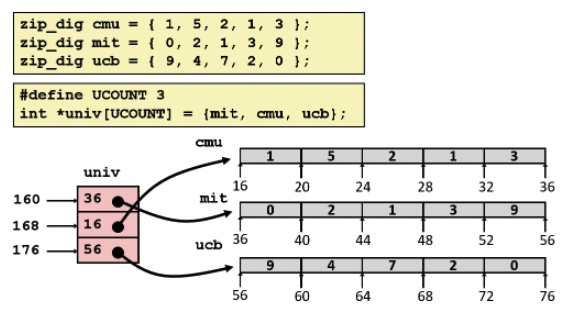
- 두 번째 차이점은 univ[i][j]에 접근할 때는 메모리 접근이 두 번 필요하다. univ[i]에 저장되어 있는 포인터를 읽고 나서, 그것에 인덱스 값을 더하여 얻은 주소로 다시 접근해서 값을 가져와야함.
- 다차원 배열은 메모리를 한번 접근해서 포인터 연산을 해준뒤 값을 가져오면 되지만, 멀티-레벨 배열은 마치 포인터 배열같은 느낌? univ는 univ배열 첫 요소의 주소 값인데 mit는 또 주소값이기 때문에 mit의 값을 가져오려면 주소에 접근한 주소를 다시 접근하는 느낌? (지극히 개인적인 느낌, 아닐 수도 있음)
구조체
- 구조체도 배열과 마찬가지로 요소들이 메모리 공간에 연속적으로 할당되며(다만 정렬 원칙을 따르기 위해 요소들 사이에 빈 공간이 삽입될 수는 있음) 할당이 되는 순서는 구조체 내에서 선언되는 순서를 그대로 따른다.
- 그저 메모리 상에 데이터들을 연속적으로 할당하고 그것에 접근할 뿐
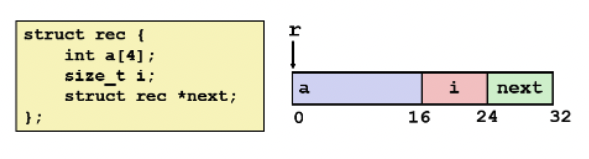
- 결국 구조체도 배열과 마찬가지로 구조체의 시작 주소에 해당 요소의 오프셋을 더함으로써 접근하고자 하는 요소의 주소를 계산한다. (구조체 요소의 접근을 위한 오프셋 정보들은 컴파일러 타임에 컴파일러에 의해 파악된다.)
x86-64 메모리 레이아웃
- 메모리 레이아웃이란 프로그램이 실행될때 해당 프로그램의 데이터와 코드가 어느 곳에 어떻게 할당되는지를 나타내는 도식
- 엄밀하게는 프로그램의 데이터와 코드가 로드되는 가상 주소 공간의 구조를 나타냄.
  - 스택 : 8MB의 공간 제한이 있다. 지역변수 등의 함수 내 지역 데이터가 저장되는 영역
  - 힙 : 동적으로 할당되는 데이터들이 위치하는 영역. (malloc, calloc 함수 등이 호출될 때 사용됨
  - 데이터 : 정적으로 할당되는 데이터들이 위치하는 영역, 전역변수, static 변수, 그리고 문자열 등의 상수가 이곳에 저장됨
  - 텍스트, 공유라이브러리 : 프로그램 코드에 해당하는 명령어들이 순차적으로 저장되는 읽기 전용 영역. 프로그램 실행 파일의 코드는 텍스트 영역, 공유 라이브러리의 코드는 별도의 공간에 로드된다.

알고리즘 마지막주였다. 시험은 한 문제도 풀지 못했다. dp에서 규칙찾는게 너무 어려웠고, dp테이블을 어떻게 만들어야할지에 대한 감이 아직 잘 안잡힌것같다. 문제를 많이 접해봐야겠다. 알고리즘 주차가 끝나고 C언어가 시작된다. 예전에 피신에서 했던 기억을 살려서 차근차근 하나씩 구현해나가야겠다. 알고리즘 주차가 끝나더라도 “느슨하게 끝까지”라는 모토로 만들어진 스터디에서 매일 한문제씩 기초부터 다시 잡아볼것이다!