algorithm

설명 DP(동적 계획법)를 간단히 설명하자면 원래 문제를 하위 문제들로 나누고, 중복으로 계산되는 하위 문제들을 한 번만 계산하고 계산 결과를 재활용함으로써, 원래 문제를 효율적으로 풀 수 있게 하는 것이다. 기본적으로 중복 문제를 여러 번 계산하는 것을 막기 위해 고안된 방법이고, 따라서 각 부분 문제의 답을 메모리에 저장해놓는다. (이 때 한 번 계산한...

Java 에서의 String비교 함수:String 을 java에서 ==로 비교하지 못하는 이유는 java가 operator overloading 을 지원하지 않기 때문이다. (C++ 같은 경우 지원하기 때문에 ==로 비교가 가능함)Immutable:한번 초기화되면 st

Hash Table빠른 삽입과 탐색을 위해 hash 함수를 이용하여 데이터를 관리하는 자료 구조. Hash Set 과 Hash Map 이 있다. 원리는 다음과 같다.

"원소들을 순서대로 처리해야 할 때 좋다."FIFO: First In First Out back에 집어넣는 것을 enqueue라고 하고, front에서 꺼내오는 것을 dequeue라고 한다.동적 배열과, head를 가리키는 index로 구현할 수 있다.하지만 그냥 배열

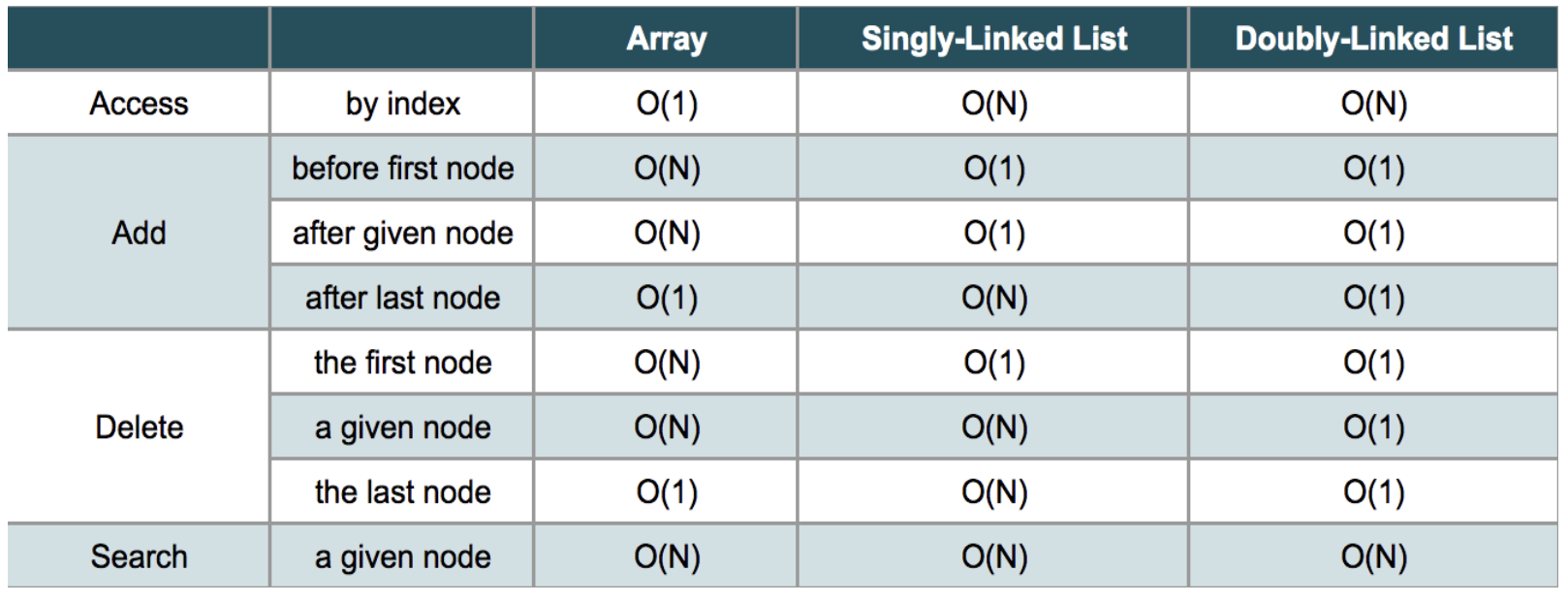
Linked List 노드들은, reference field 로 연결된 독립 객체들이다.보통 첫번째 노드(head)를 써서 list 전체를 나타낸다.Linked List 노드 = 값 + (다음 노드로 연결되는) reference field접근: O(N) 시간 (head

트리의 각 노드 = 루트 값 + 자식 노드에 대한 참조 목록이진 트리: 각 노드가 최대 두 개의 자식을 갖는 트리 자료 구조root -> left subtree -> right subtree(FBADCEGIH)재귀 시간복잡도: O(N) (모든 노드를 한번씩만 방문)공간

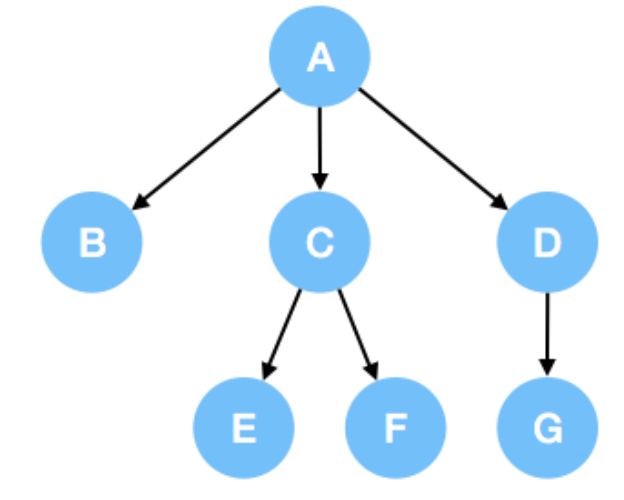
Binary Tree 때 배웠던 순회 중 In-order traverse(중위 순회)에 대한 정의는 없다.(1) Preorder Traversal: A->B->C->E->F->D->G(2) Postorder Traversal: B->E->F->C->G->D->A(3)

자신을 서브루틴으로 호출하는 함수를 사용하여 문제를 해결하는 방법자신을 호출할 때마다 주어진 문제를 여러 개의 하위 문제로 축소하는 것이 핵심이다. 재귀 호출은 더 이상 재귀를 사용하지 않고 하위 문제를 해결할 수 있는 지점에 도달할 때까지 계속된다.재귀 함수를 구현하

이진 트리의 특수한 형태. 다음의 조건을 만족한다. (재귀적 정의)(1) 각 노드의 값은 왼쪽 서브트리의 모든 값보다 크거나 같다.(2) 각 노드의 값은 오른쪽 서브트리의 모든 값보다 작거나 같다. 중위 순회 (Inorder traversal, left -> root

트리에서의 용어 > - 노드의 깊이: 루트 노드에서부터의 간선의 갯수 노드의 높이: leaf 노드까지의 간선의 최대 갯수 트리의 높이: 루트 노드의 높이 정의 임의의 항목 삽입/삭제에 대해 자동으로 높이를 작게 유지하는 BST. N개의 노드를 가진 균형 BST의 높이

Graph: vertex 와 edge 로 구성된 비선형 자료 구조 Vertex: 정점Edge: 두 vertex 사이의 연결Path: 한 vertex에서 다른 vertex로 이동하는 vertex의 순서Path Length: 경로에 있는 간선의 수Cycle: 시작점과 끝점

DFS 용도 (1) 그래프에서 모든 정점 탐색 시간 복잡도: O(V+E) 공간 복잡도: O(V) (일직선이면 모든 정점 다 들어가야 함) (2) 그래프에서 두 정점 사이의 모든 경로 탐색 시간 복잡도: O((V-1)!) (완전 그래프에서의 찾은 경로 수 O((V−2)

Spanning Tree (신장 트리)그래프의 최소 연결 부분 그래프(무방향 그래프에서) 최소 간선 수로 모든 정점이 연결된 그래프무방향 그래프는 여러 개의 스패닝 트리를 가질 수 있다.Minimum Spanning Tree가중치가 있는 무향 그래프에서가능한 최소의 간

최단 경로 문제에서 BFS 를 사용하지만, BFS는 무가중치 그래프에서만 문제를 해결 가능하다. 가중치 그래프에서 최단 경로를 찾아야한다면 어떻게 해야 할까? Single Source Shortest Path 알고리즘을 사용하면 된다. 두 가지 구현이 있다.(\* 음수

유향(directed) 비순환(acyclic) 그래프에서 정점 간의 필요한 순서에 따라 선형 정렬

용도 최대 혹은 최소 원소를 효율적으로 찾을 수 있다.