5주차 회고
2021.12.02 THU ~ 12. 09 THU
5주차의 목표는 RBtree를 C언어로 구현해내는 것이었다.
다들 C언어는 생소해서, 우리 조는 우선 토요일정도까지는 각자 C기본 문법을 공부했다.
내가 도움 받은 영상은 여기이다.
한 달간의 알고리즘 과정이 끝난 후라 사람들과 맛있는 것도 먹으러 가고 했던지라, 진도가 생각보다 느리게 나갔다.
기초문법을 빠르게 훑어본 후 (포인터 부분은 더 꼼꼼하게 볼 걸 그랬다.)
유튜브에 나오는 여러 RBtree에 대한 영상들과 구글링으로 나오는 글들,
그리고 INTRODUCTION TO ALGORITHMS 교재에 나오는 RBtree 파트 부분을 읽기 시작했다.
교재에는 RBtree의 코드가 슈도코드로 나와있는데, 이 것을 이해만 하면 코드로 구현할 수 있었다.
아, 그리고 12.6부터 정글 멤버 맘 맞는 몇 명끼리 모여 자체적으로 파이썬 알고리즘 인터뷰 라는 교재를 이용한 알고리즘 스터디를 만들어서 참여하기 시작했다. 덕분에 매일매일 알고리즘 1~2문제씩 풀고 있다.
5주차 셀프 평 : 조바심 내지 않고 차분히 잘 해냈다.
RBtree 최종 구현 코드
https://github.com/Yerimi11/rbtree-lab/blob/main/src/rbtree.c
malloc, calloc
malloc : memory allocation
calloc : contiguous allocation
The malloc() function allocates memory and leaves the memory uninitialized,
whereas the calloc() function allocates memory and initializes all bits to zero.
전에는 calloc이 단위 data 크기에 따라 address alignment를 조절했기 때문에 struct나 그 array는 calloc으로 할당받아야 했습니다. malloc은 byte 단위로도 할당할 수 있기 때문에 64bit interger와 같이 align되어야 하는 기억공간을 할당받을 때 한 두 바이트 어긋난 address로 할당받을 경우 Bus error가 났습니다.
요즘에는 x86의 경우 malloc이 double word align된 address를 할당하기 때문에 alignment 문제가 사라졌고, 도리어 initialize 하는 과정도 시간낭비다 하여 calloc 대신 malloc을 써야 한다고 주장하는 사람도 있는 걸로 압니다. /코치님.
콜록은 초깃값이 0이다.
RBtree 삭제 조건 (Fix_up)
insert할 때 처럼 fix_up 과정을 거쳐야 한다.
insert는 노드의 위치를 찾아갔지만 delete는 좀 다르다.
3가지의 케이스가 있다.
Delete Case 3
1) 왼쪽이 nil
2) 오른쪽이 nil - 왼쪽이 노드일 수도 있고 nil일 수도 있다
3) 둘 다 노드
이다.
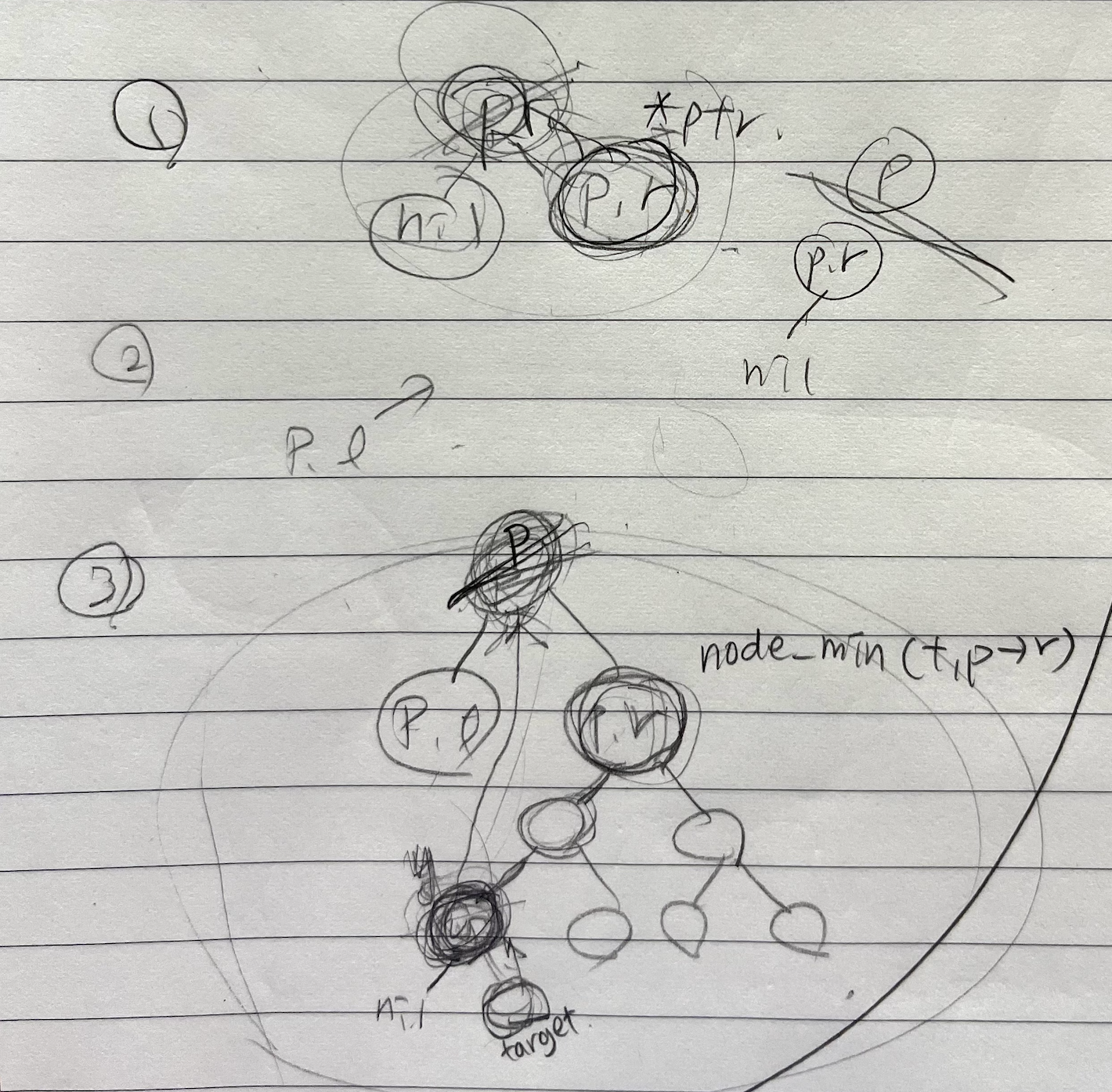
1) 왼쪽이 nil
p를 없앤다 - p를 빼고 p.right을 넣으면 끝
p.right은 ptr이 되어 fixed-up을 할 때 기준이 되는 노드가 된다.
2) 오른쪽이 nil
1)과 같은 방법으로 처리
3) 둘 다 노드
y는 p에 들어가도 된다. 왜냐? p보다 오른쪽에 있는 것들은 왼쪽보다 크니까 & p.r 자식 노드들 중의 최솟값인 y만 들어갈 수 있다 (우측에서 가장 작은 수지만 왼쪽보단 크니까)
(1) p를 날린다
(2) y는 최소니까 y의 왼쪽자식은 무조건 nil. y.r은 있을 수도 없을수도. 있다고 가정.
(3) 1),2)케이스처럼 y.r을 y에 넣고, 그 값을 p노드로 보낼 수 있음
그리고 y가 p에 들어가고 색을 p랑 맞춰주면 rbtree조건은 그대로 유지할 수 있음.
(4) 그리고나서 y.r을 ptr로 지정
(y의 색을 origincolor변수에 넣어서 구별해줌. y의 색깔을 아는 것이 중요)
(5) 결국 셋 다 nil노드를 가지고 있는 노드를 지우는 케이스가 됨. -> 이걸 처리해주는 함수를 하나로 만들자 : RB_TRANSPORT
erase(delete) 코드
int rbtree_erase(rbtree *t, node_t *p) {
if(p == NULL){
return 0;
}
node_t *y= p;
node_t *ptr; // fixed_up의 기준이 될 노드
color_t y_original_color = p->color;
// case1 : 왼쪽 노드가 nil일 때
if (p->left == t->nil){
ptr = p->right;
RB_TRNASPLANT(t, p, p->right);
}
// case2 : 오른쪽 노드가 nil일 때
else if (p->right == t->nil){
ptr = p->left;
RB_TRNASPLANT(t, p, p->left);
}
// case3 : 왼쪽, 오른쪽 둘 다 노드일 때 (not nil)
else {
// y는 p.r을 루트로 하는 서브 트리의 최소키를 가지는 노드
y = node_min(t, p->right);
// ptr을 y->right로 바꿔주고 color를 위에서 찾은 y의 color로 변경시켜 준다.
y_original_color = y->color;
ptr = y->right;
// case1 : p의 자식이 y일 때
if (y->parent == p){
ptr->parent = y; // fixup 후 y가 nil이 됐을 수도 있는데 nil은 p를 가리킬 수 없으니 ptr가 부모를 알아야 하는 상황에서 알 수 없어서 정해줌
}
else {
// 그 외 케이스 : y의 부모노드를 y->right와 연결시킨다.
RB_TRNASPLANT(t, y, y->right);
// p의 오른쪽 노드와 y를 연결시킨다.
p->right->parent = y;
y->right = p->right;
}
// p의 부모노드를 y와 연결시킨다.
RB_TRNASPLANT(t, p, y);
// p의 왼쪽노드를 y와 연결시킨다.
y->left = p->left;
p->left->parent = y;
y->color = p->color;
}
if (y_original_color == RBTREE_BLACK){
RB_ERASE_FIXUP(t, ptr);
}
free(p);
// p = NULL;
return 0;
}RB_TRANSPORT 함수
RB_TRANSPORT(T, U, *V) / u : 버려질 노드, v : 대체될 노드
(위에 케이스 3개에서는 p = u / p.r,p.l = v 혹은 y = u / y.r = v )
u.p
u
v 서로 양방향이라고 가정했다가v->u를 지우고 v를 u.p에 연결시킴. v->p = u->p 두 노드가 같으면
u.p도 v에 연결시키면 u로는 들어오는 노드가 없으니 떨어졌다고 침. (u 고립됨)
즉, 1)케이스에서 p가 나가고 p.r이 들어왔다고 보면 됨. 그 후 free(p)하면 끝.
[fixed-up 이전의 erase 끝]
+) rb_trans(p,y ) : P의 부모노드를 y와 연결..
transport(transplant) 코드
transplant나 transport나 상관 없다
void RB_TRNASPLANT(rbtree *t, node_t *u, node_t *v){
v->parent = u->parent;
// root
if (u->parent == t->nil){
t->root = v;
}
// left
else if (u == u->parent->left){
u->parent->left = v;
}
// right (u->parent->right == u 생략)
else {
u->parent->right = v;
}
// v->parent = u->parent;
}ERASE FIXED_UP 함수
https://assortrock.com/88 참고. 짱
ERASE_FIXUP 코드
void RB_ERASE_FIXUP(rbtree *t, node_t *target){
node_t *u;
// fix가 시작되는 조건
while(target != t->root && target->color == RBTREE_BLACK){
//기준이되는 노드가 왼쪽일 때
if(target->parent->left == target){
u = target->parent->right;
//case1: uncle is red
if(u->color == RBTREE_RED){
//형제를 검은색으로 부모를 빨간색으로 칠한다. 부모노드를 기준으로 좌회전한다.
u->color = RBTREE_BLACK;
target->parent->color = RBTREE_RED;
left_rotate(t, target->parent);
u = target->parent->right;
}
//case2: uncle is black with two black child
if(u->left->color == RBTREE_BLACK && u->right->color == RBTREE_BLACK){
//형제노드만 빨간색으로 만들고 타겟을 부모로 변경한다.
u->color = RBTREE_RED;
target = target->parent;
}
else { // 자식 중 최소 한개는 빨간색이다.
//case3: uncle is black with red color left child and black color right child
if(u->right->color == RBTREE_BLACK){
// 형제 노드를 빨간색으로, 형제 노드의 왼쪽 자식을 검은색으로 칠하고 형제노드를 기준으로 우회전한다.
u->color = RBTREE_RED;
u->left->color = RBTREE_BLACK;
right_rotate(t, u);
u = target->parent->right;
}
//case4: uncle is black with red color right child
// 부모 노드의 색을 형제에게 넘긴다. 부모노드와 형제 노드의 오른쪽 자식을 검은색으로 칠한다. 부모 노드 기준으로 좌회전한다.
u->color = target->parent->color;
target->parent->color = RBTREE_BLACK;
u->right->color = RBTREE_BLACK;
left_rotate(t, target->parent);
target = t->root;
}
}
//기준이 되는 노드가 오른쪽 일때
else{
u = target->parent->left;
//case1: uncle is red
if(u->color == RBTREE_RED){
//형제를 검은색으로 부모를 빨간색으로 칠한다. 부모노드를 기준으로 좌회전한다.
u->color = RBTREE_BLACK;
target->parent->color = RBTREE_RED;
right_rotate(t, target->parent);
u = target->parent->left;
}
//case2: uncle is black with two black child
if(u->right->color == RBTREE_BLACK && u->left->color == RBTREE_BLACK){
//형제노드만 빨간색으로 만들고 타겟을 부모로 변경한다.
u->color = RBTREE_RED;
target = target->parent;
}
else { // 자식 중 최소 한개는 빨간색이다.
//case3: uncle is black with red color right child and black color left child
if(u->left->color == RBTREE_BLACK){
// 형제 노드를 빨간색으로, 형제 노드의 왼쪽 자식을 검은색으로 칠하고 형제노드를 기준으로 우회전한다.
u->color = RBTREE_RED;
u->right->color = RBTREE_BLACK;
left_rotate(t, u);
u = target->parent->left;
}
//case4: uncle is black with red color left child
// 부모 노드의 색을 형제에게 넘긴다. 부모노드와 형제 노드의 오른쪽 자식을 검은색으로 칠한다. 부모 노드 기준으로 좌회전한다.
u->color = target->parent->color;
target->parent->color = RBTREE_BLACK;
u->left->color = RBTREE_BLACK;
right_rotate(t, target->parent);
target = t->root;
}
}
}
target->color = RBTREE_BLACK;
}find 함수
키값보다 큰가작은가해서 좌우로 돌아다니다가
키값이랑 같으면
ptr의 키가 키(받은 키랑 같으면) 포인터를 리턴
ptr->key == key
return ptr
아니면 null
혹은 재귀로 찾는 법도 있음
find 코드
node_t *rbtree_find(const rbtree *t, const key_t key) {
node_t *tmp = t->root; // 돌아다니면서 찾음
// tmp(이동하는 거)가 맨 끝이 아니고 && 찾을 목표 key값도 아직 아니면 while
// 맨끝에 nil까지 가거나, 찾고자하는 key를 찾으면 종료
while(tmp != t->nil && tmp->key != key) {
if (tmp->key > key) { // 찾을 키값보다 지금 위치의 키값이 더 크면
tmp = tmp->left; // 더 작은 값을 찾아야하니까 왼쪽으로
}
else{
tmp = tmp->right;
}
}
if (tmp->key == key){ // 키값이 같을 때
return tmp;
}
return NULL;
}array 함수
중위순회 재귀로..
-> 중위순회를 하면서 값을 리스트에 담으면 오름차순으로 정렬된 상태로 담을 수 있다
함수 하나 더 만들어서 트리노드를 함수에 보내서 시작하게하고 인덱스 0 부터 시작해서.. 재귀적으로
트리노드 왼쪽으로 보내고 (왼쪽-나-오른쪽 순서니까) / 가운데 arr에 넣는 식 쓰고 / 그 다음 노드의 오른쪽을 부르는 함수쓰는데
이 때 왼쪽함수나 오른쪽함수가 nil이면 들어갈 필요 없게 / 아니면 함수 자체가 들어오자마자 노드가 nil일 경우 바로 리턴
array 코드
int inorder_array(node_t *p, key_t *arr, const rbtree *t, int i){
if (p == t->nil) {
return i;
}
i = inorder_array(p->left, arr, t, i);
arr[i++] = p->key;
i = inorder_array(p->right, arr, t, i);
return i;
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n){
// int i = 0;
node_t *tmp = t->root;
inorder_array(tmp, arr, t, 0);
return 0;
}rbtree구현 오류 수정
오류 1
test-rbtree: test-rbtree.c:51: test_find_single: Assertion `q == NULL' failed.
make[1]: *** [Makefile:6: test] Aborted (core dumped)
make[1]: Leaving directory '/home/ubuntu/rbtree-lab/test'
make: *** [Makefile:13: test] Error 2find에서 wrong_key가 나왔을 때 null값을 반환하게 해야함
return NULL;
tmp->key != key 를 쓰려면
if tmp = key 일때 key를 보내고
else return NULL
코드 수정
node_t *rbtree_find(const rbtree *t, const key_t key) {
node_t *tmp = t->root; // 돌아다니면서 찾음
// tmp(이동하는 거)가 맨 끝이 아니고 && 찾을 목표 key값도 아직 아니면 while
// 맨끝에 nil까지 가거나, 찾고자하는 key를 찾으면 종료
while(tmp != t->nil && tmp->key != key) {
if (tmp->key > key) { // 찾을 키값보다 지금 위치의 키값이 더 크면
tmp = tmp->left; // 더 작은 값을 찾아야하니까 왼쪽으로
}
else{
tmp = tmp->right;
}
}
if (tmp->key == key){ // 키값이 같을 때
return tmp;
}
return NULL;
}—————수정 완료
오류2
test-rbtree: test-rbtree.c:113: test_minmax: Assertion `q->key == arr[n - 1]' failed.
make[1]: *** [Makefile:6: test] Aborted (core dumped)
make[1]: Leaving directory '/home/ubuntu/rbtree-lab/test'
make: *** [Makefile:13: test] Error 2(*i)++; 쓰면 가능
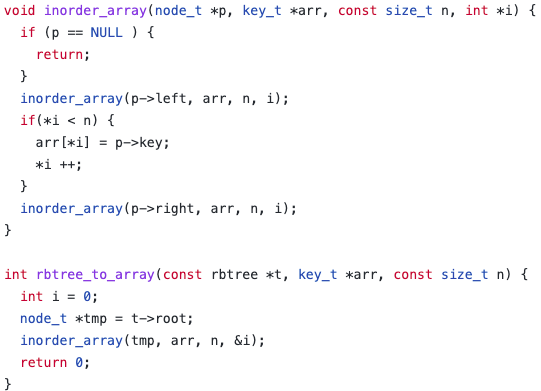
이 코드에서 변경함.
코드 수정 1 (에러)
int inorder_array(node_t *p, key_t *arr, const rbtree *t, int i) {
if (p == t->nil) {
return i;
}
i = inorder_array(p->left, arr, t, i);
arr[i++] = p->key;
i = inorder_array(p->right, arr, t, i);
return i;
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
// int i = 0;
node_t *tmp = t->root;
inorder_array(tmp, arr, t, 0);
return 0;
}같은 에러 발생
그래서 인서트 문제였음.
insert 아예 코드 교체함
코드 수정 2 (insert 최종)
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *new_node = malloc(sizeof(node_t));
node_t *x = t->root;
node_t *y = t->nil;
new_node->key = key;
while (x != t->nil){
y = x;
if (new_node->key < y->key){
x = x->left;
}
else {
x = x->right;
}
}
new_node->parent = y;
if (y == t->nil){
t->root = new_node;
}
else if (new_node->key < y->key){
y->left = new_node;
}
else {
y->right = new_node;
}
new_node->left = t->nil;
new_node->right = t->nil;
new_node->color = RBTREE_RED;
RB_INSERT_FIXUP(t, new_node);
return new_node;
}
코드 리뷰 피드백

void?
원래 과거에 컴퓨터 메모리가 부족해서 메모리 관리를 잘 해야 할 때는 main을 void로 사용했습니다. int main으로 return 0를 하는 메모리 하나라도 아끼기 위함이죠. 아마 강의자료를 작성하신 분이 그런 습관이 있으신 것 같습니다.
만약에 return 0;를 사용하고 싶으시다면 void main을 int main으로 바꿔주신 뒤 return 0;를 사용하시면 됩니다. int main에 따라오는 return 0는 main이 종료된 뒤 main을 호출한 곳에 0만 리턴하겠다는 의미입니다. 초보자 수준에서는 크게 신경쓰시지 않아도 되는 부분이며 관례처럼 사용하신다고 보면 됩니다.
int도 되고, char도 되고.. 다 되는 형태라고 보면 된다
