
글을 시작하기 전에
velog는 내가 평소 UX와 UI가 예쁘고 편하다고 생각했던 블로그 중 하나였다.
나의 첫 블로그, 첫 글을 velog를 통해 만들 수 있어서 기분이 좋다.
이 글을 시작으로 velog에서 많은 사람들과 소통할 수 있었으면 좋겠다.
🙏 만약 잘못된 부분이 있거나, 부족한 부분이 있다면 댓글로 알려주세요!
1. 유클리드 호제법이란?
유클리드 호제법은 두 수의 최대공약수를 구하는 알고리즘이다.
유클리드(Euclid)에 의해 기원전 300년경에 발견된 가장 오래된 알고리즘이다.
호제법이란? 두 수가 서로 상대방 수를 나누어서 결국 원하는 수를 얻는 알고리즘을 말한다.2. 1112와 695의 최대공약수 계산하기
일반적인 방법
일반적으로 최대공약수를 구하기 위해선 먼저 소인수분해를 해야한다.
1112 = 139 X 2 X 2 X 2
695 = 139 X 5두 수를 소인수분해한 후, 공통된 소수를 찾으면 된다. 이를 통해 두 수의 최대공약수(GCD)는 139인 것을 알 수 있다.
이 방법은 수가 커질수록 소인수분해하기 어려워진다는 단점이 있다.
이때, 유클리드 호제법을 사용하면 조금 더 효율적으로 최대공약수(GCD)를 구할 수 있다!
유클리드 호제법 사용하기
💡 유클리드 호제법을 이해하기 위해서는 MOD연산에 대해 알고 있어야 한다.
MOD연산이란? 두 값을 나눈 나머지를 구하는 연산!
먼저, 큰 수를 작은 수로 나눈 나머지를 구한다. 즉, MOD 연산을 한다.
1112 mod 695 = 417그 다음, 나눴던 수와 나머지로 또 MOD 연산을 한다.
695 mod 417 = 278이 과정을 계속 반복한다.
417 mod 278 = 139
278 mod 139 = 0나머지가 0이 됐을 때, 마지막 계산에서 나누는 수로 사용된 139가 1112와 695의 최대공약수가 된다.
간단하게 말하면, 유클리드 호제법은 MOD연산을 반복하면 된다!
3. 유클리드 호제법 이해하기
어떻게 유클리드 호제법으로 최대공약수(GCD)를 구할 수 있을까?
1112와 695를 막대의 길이로 표현한 뒤에, 두 수의 최대공약수 N으로 나눠보았다.
위에서 우리는 최대공약수가 139라는 것을 알았기 때문에 8칸, 5칸으로 나누었지만 실제로는 모른다고 생각하면 된다.
하지만, 1112와 695가 최대공약수 N의 배수라는 것은 알고 있다.
위에서 한 대로, 1112와 695를 반복해서 MOD 연산한다.
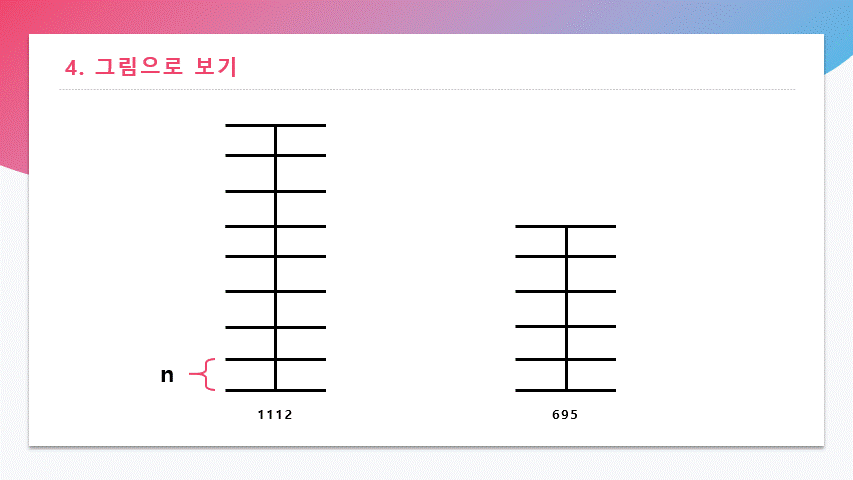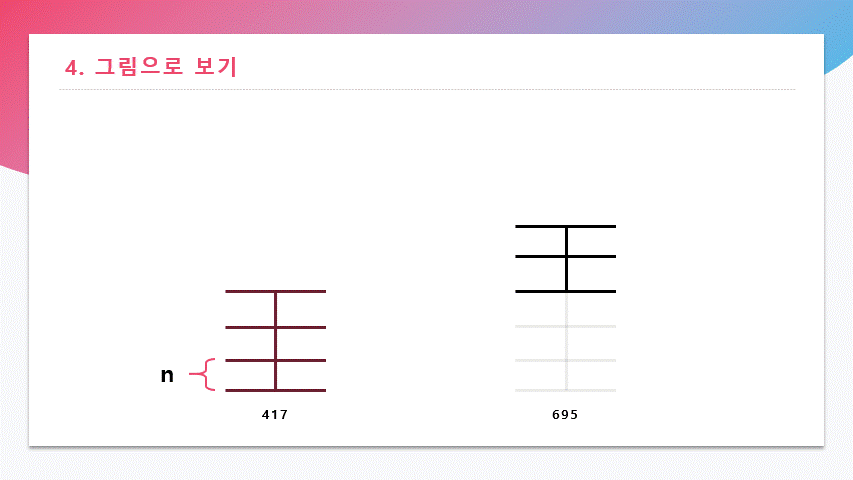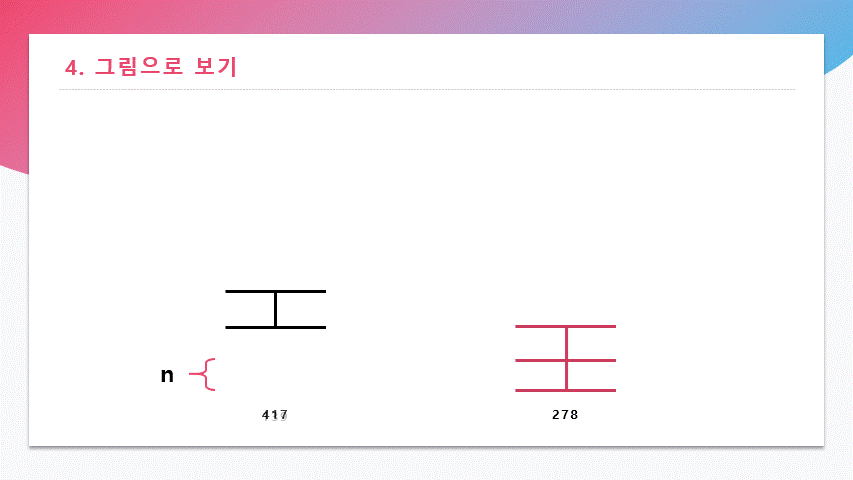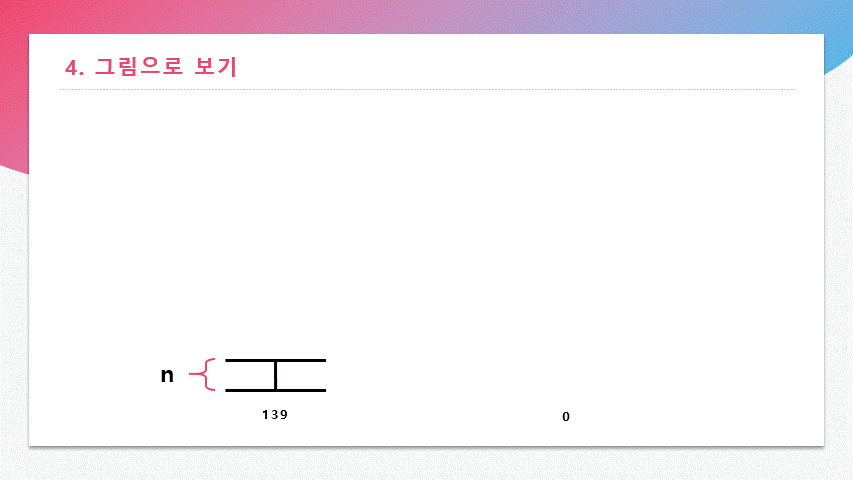
이 그림을 통해 연산 중에 나온 나머지
417, 278, 139도 모두 N의 배수인 수라는 것과 같은 최대공약수를 가진다는 것을 알 수 있다.
278은 139로 나누어지므로 나머지가 0이 된다.
이때, 최대공약수 N이 139라는 것을 알 수 있다.
유클리드 호제법은 나눗셈만 반복해서 최대공약수(GCD)를 구할 수 있다.
두 개의 수가 아무리 커도 정해진 순서로 계산하면 효율적으로 최대공약수를 구할 수 있다.
[참고] 알고리즘도감, [그림] 자체제작
4. 코드
유클리드 호제법은 반복문과 재귀함수를 통해 쉽게 표현할 수 있다.
C언어로 간단하게 작성해봤다. (조건: a>b)
반복문
int GCD(int a, int b){
int tmp;
while(b){ //b가 0이 될 때까지
tmp = a % b;
a = b;
b = c;
}
return a;
}재귀함수
int GCD(int a, int b){
return b ? GCD(b, a % b) : a;
}5. 관련 문제
유클리드호제법을 이용하여 해결할 수 있는 알고리즘 문제다.
- 프로그래머스 - N개의 최소공배수
https://programmers.co.kr/learn/courses/30/lessons/12953
글을 마치며
처음 글을 쓰면서, 글을 쓰는 것이 생각보다 더욱 어렵다는 것을 알게 되었다.
그동안 내가 읽었던 글을 쓰신 분들께 너무나 감사하다😢
앞으로 운영체제, 알고리즘 등 내가 알게된 것들을 여러 사람들과 나눌 수 있었으면 좋겠다.




잘보고가요!