[프로그래머스] 소수 찾기 - JS

문제

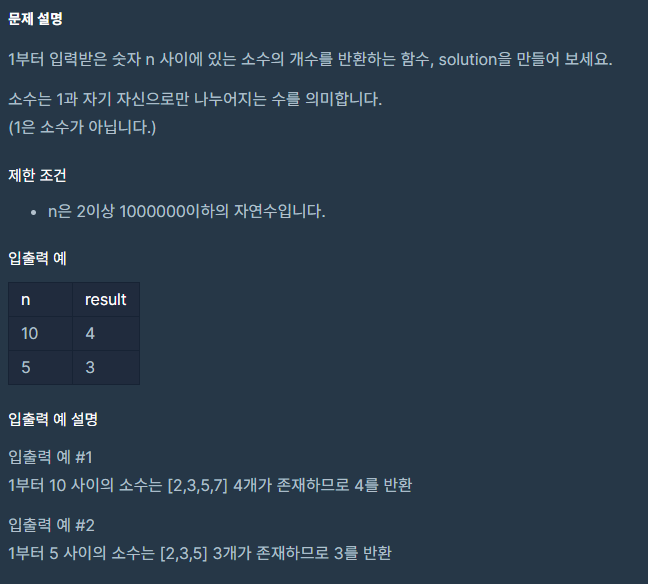
문제 자체는 간단했다.

• 2부터 n까지 수를 확인한다.
• 그 수의 루트(sqrt)까지 확인한다.
  - n % 루트(sqrt)한 수가 0이면 소수가 아니므로 flag에 기록한다.

처음에는 이러한 방식으로 코드를 짜기 시작했다.
코드 자체는 짜고보니 매우 간단했지만, 효율성 테스트에서는 0점을 받았다.

그래서 찾아보니 '에라토스테네스의 체'라는 알고리즘이 있어 공부했고, 이를 토대로 코드를 작성해 제출했다.

초반 코드

사실 이 코드에서 sqrt값에 i+1이 아닌 i를 넣어주면 제대로된 값이 나오지않는데, 그 이유를 잘 모르겠다.
그래서 추후 다시 코드를 봐야 할 것 같다.

function solution(n){
    var answer = 0;
    let flag = 0;

    for(let i=n; i>1; i--){
        for(let j=2; j<Math.sqrt(i+1); j++){
            if(i%j == 0){
                flag = 1;
                break;
            }
        }
        if(flag == 0)
            answer++
        flag = 0;
    }

    return answer;
}

console.log(solution(5))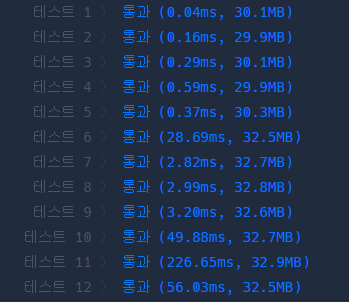

개선된 코드

let PrimeArray = [];

function Eratos(n){
    if(n<=1) return;

    for(let i=2; i<=n; i++){
        PrimeArray[i] = true
    }

    for(let i=2; i*i <=n; i++){
        if(PrimeArray[i])
            for(let j=i*i; j<=n; j+=i)
                PrimeArray[j] = false;
    }
}

function solution(n) {
    var answer = 0;
    Eratos(n)
    for(let i=2; i<=n+1; i++){
        if(PrimeArray[i] == true){
            answer++
        }
    }
    
    return answer;
}

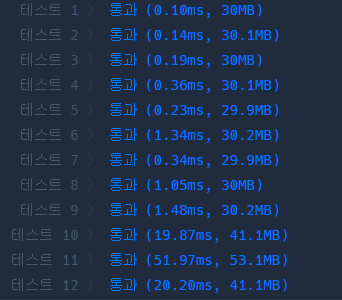
코드 개선 후 테스트 결과가 무척 좋아진 것을 확인할 수 있다.

위키백과에 있는 코드를 거의 그대로 사용했기 때문에 좀 더 완벽한 이해가 필요할 듯 싶다.