백준 2110 문제 / 책 369p

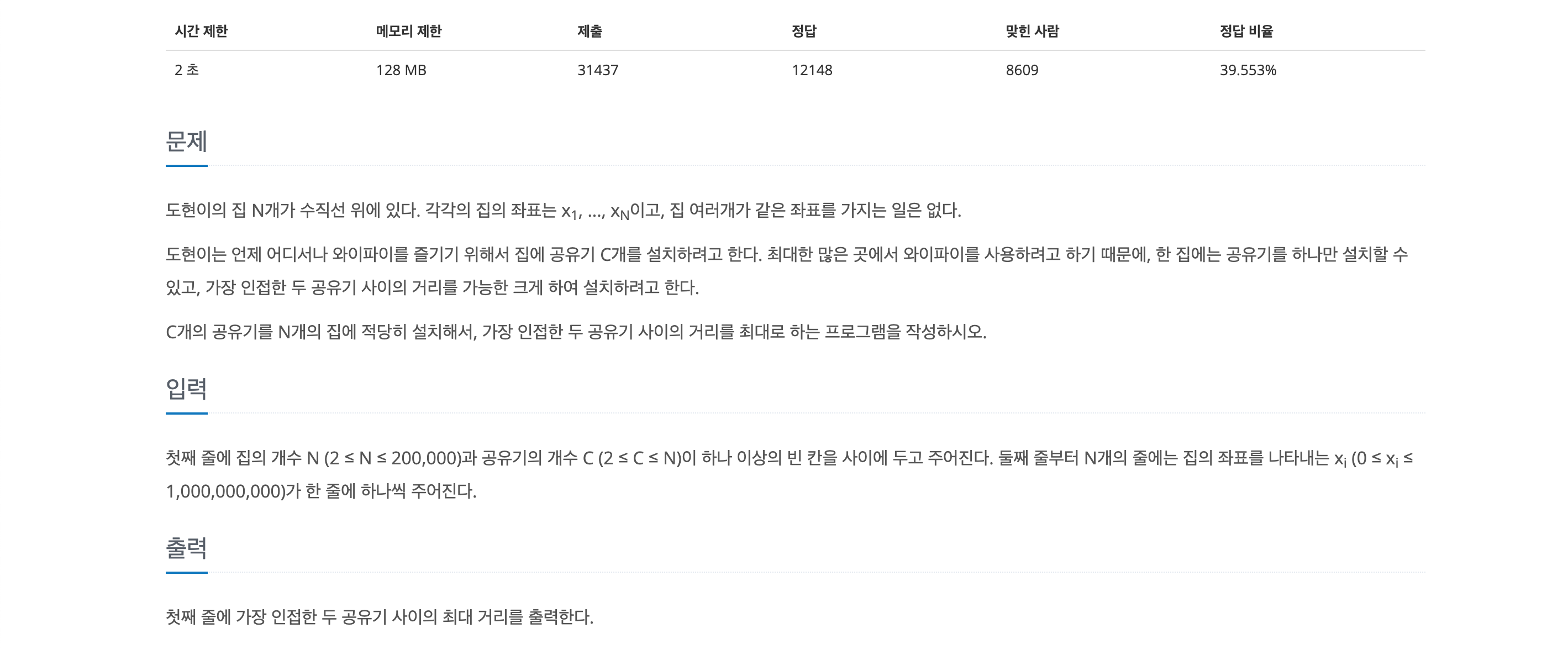
문제

풀이

처음보고 든 생각

• 적당한 수를 이진탐색을 찾는 떡 자르기 문제의 parametic search 가 생각났다.
  아마 맞지 않을까?

• '적당한' 의 기준은 아마 '가장 인접한 두 공유기 사이의 거리를 최대로' 일 것이다.

• 집들이 일직선 상에 위치하고 있으니, 뺄셈후 절댓값 씌운 것을 거리로 활용할 것.

• 그런데 공유기가 2개가 아니라, C개이면,, , 걍 손으로 생각하는게 빠를듯
  
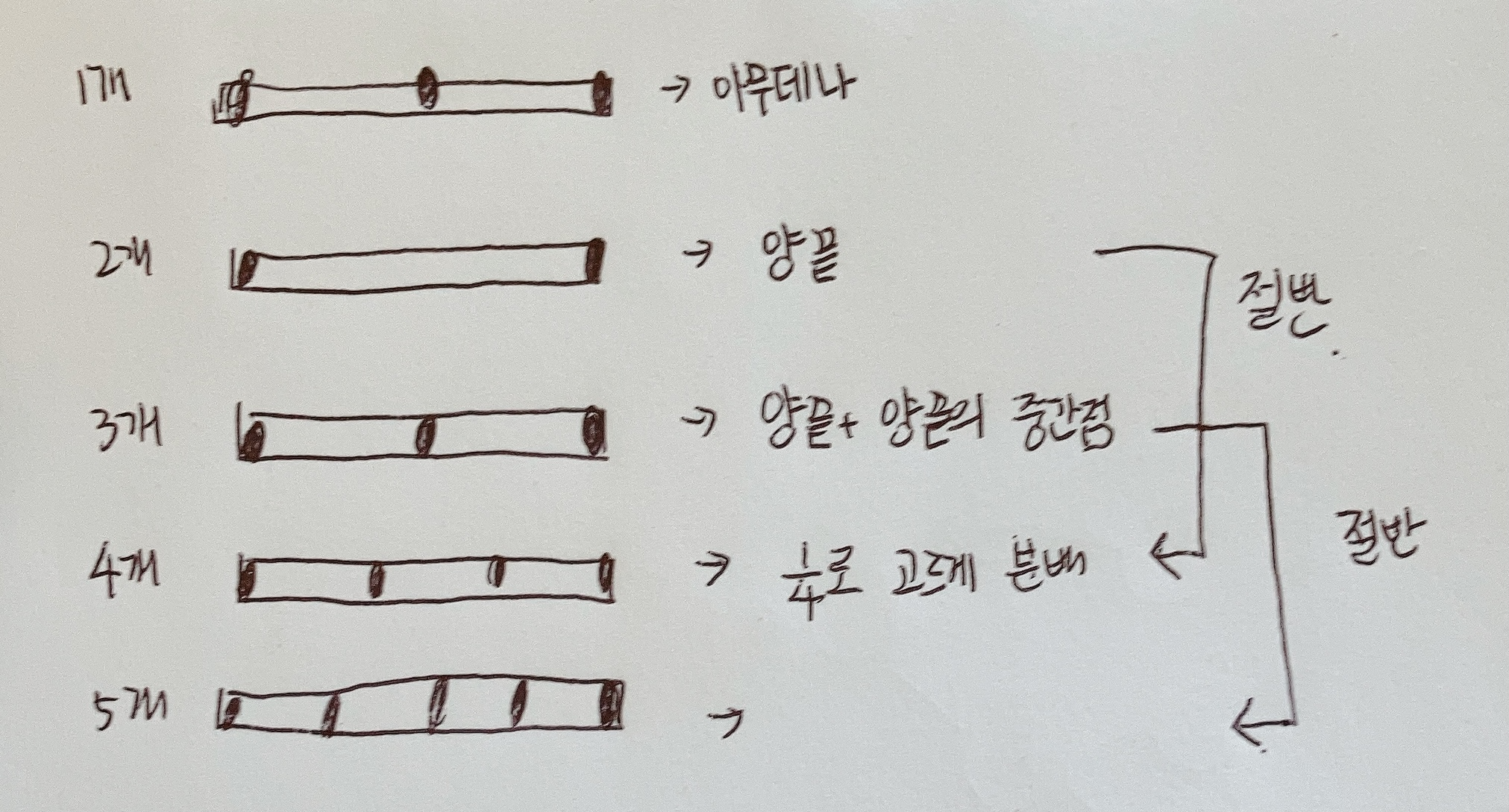
  이렇게 짝-홀 기준으로 나눠서 생각하면 안될까요

풀이 아이디어

파라매트릭 서치 유형

• 이진탐색으로 '가장 인접한 두 공유기 사이 거리'를 조절해가며, 매 순간 실제로 공유기를 설치하여 C보다 많은 갯수로 공유기를 설치할 수 있는지 체크하여 문제 해결
• '가장 인접한 두 공유기 사이의 거리'의 최댓값을 찾아야하므로, C보다 많은 갯수로 공유기를 설치할 수 있다면, '가장 인접한 두 공유기 사이의 거리'의 값을 증가시켜서, 더 큰 값에 대해서도 성립하는지 체크하기 위해 다시 탐색을 수행한다.

예시)
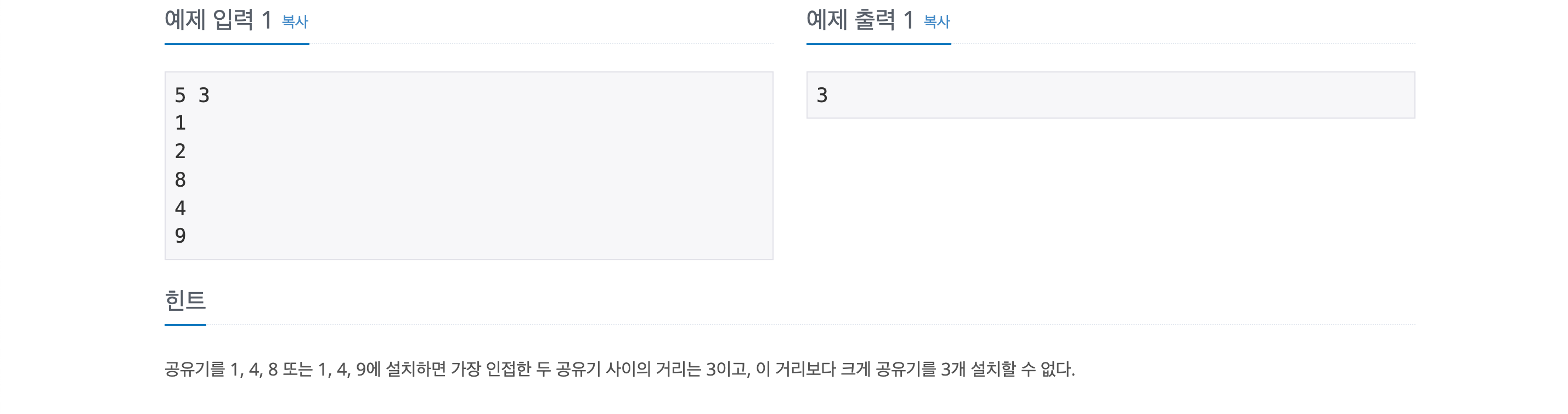
5개의 집의 좌표는 [1,2,4,8,9] 이고 공유기의 최소갯수 C=3

• 가장 인접한 두 공유기 사이 거리(gap)은 1~8까지가 될 수 있다.
  • 최대 gap = 8
  • 최소 gap = 1
• 1) 범위가 1~8이므로, gap값을 중간값인 4로 설정.
  앞에서부터 설치시, [1,2,4,8,9] 처럼 설치된다.
  이렇게 하면 공유기를 2개밖에 설치할 수 없다.
  C=3이므로 gap을 더 줄여야한다.
  범위를 [1,3] 으로 수정한다.
• 2) 범위가 1~3이므로, gap의 값을 중간값인 2로 설정.
  앞에서부터 설치시, [1,2,4,8,9]
  C=3 인데, C=3이상인 값이기 때문에,
  현재의 gap을 저장한 뒤에, gap의 값을 증가시켜서 gap이 더 커졌을 때도 가능한지 확인할 필요가 있다. 따라서, 범위가 [1,3] 인 상태에서 범위를 [3,3] 으로 수정한다.
• 3) 범위가 3~3이므로, gap의 값을 중간에 해당하는 3으로 설정한다. 이 경우, C=3인데 C=3이상의 값이기 때문에, 현재의 gap을 저장한 후, gap 값ㅇ르 ㅈ으가시켜서 gap 이 더 커졌을 때도 가능한지 확인할 필요가 있다.
  현재 범위가 3~3 이므로, 더 이상 범위를 변경할 수 없다.
  -> 따라서, gap=3이 최적의 경우.

코드

# 집의 갯수 N, 공유기의 최소 갯수 C 입력받기
n, c = list(map(int, input().split(' ')))

# 전체 집의 좌표 정보를 입력받기
array = []
for _ in range (n) :
	array.append(int(input()))
array.sort() # 이진탐색 수행을 위해 정렬 수행

start = array[1] - array[0] # 집의 좌표중에 가장 작은 값
end = array[-1] - array[0] # 집의 좌표중에 가장 큰 값
result = 0

while (start <= end) :
	mid = (start+end) // 2 # mid는 가장 인접한 공유기사이의 거리(gap)를 의미
	value = array[0]
	count = 1
	# 현재의 mid값을 이용해 공유기를 설치
	for i in range(1, n) # 앞에서부터 차근차근 설치
		if array[i] >= value + mid :
			value = array[i]
			count += 1
	if count >= c : #C개 이상의 공유기를 설치할 수 있는 경우, 거리를 증가
		start = mid + 1
		result = mid #최적의 결과를 저장
	else : #C개 이상의 공유기를 설치할 수 없는 경우, 거리를 감소
		end = mid - 1

print(result)

느낀점

먼가,, 아직 잘 이해가 안된다.
[ ] 손으로 다시그리기
[ ] 다시 치기