1. 관계 데이터 모델
⭐ 릴레이션(relation) : 행과 열로 구성된 테이블
- 수학의 집합에서 나온 개념
- 테이블 : 릴레이션의 시각적인 표현 방법
⭐ 관계( relationship)
- 릴레이션(테이블)내의 관계 : 릴레이션 내의 데이터들의 집합으로 표현
- 릴레이션(테이블)간의 관계 : 릴레이션을 식별 가능한 값을 이용해 표현 -- > 관계 데이터 모델을 다른 데이터 모델과 구분하는 특징
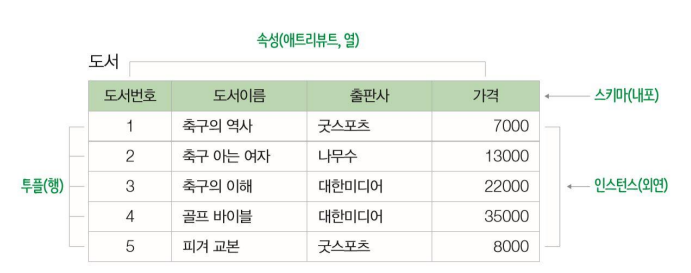
⭐ 릴레이션 스키마(=내포 schema) : 관계 데이터베이스의 릴레이션이 어떻게 구성되는지, 어떤 정보를 담고 있는지에 대한 기본적인 구조를 정의
테이블의 헤더에 나타나며 각 데이터의 특징을 나타내는 속성, 자료타입 등의 정보를 담고 있음.
그러나 컴퓨터로 처리되는 과정에서 데이터베이스는 속성 이름만으로 어떤 형태의 자료가 있는지 알 수 없으므로 도메인이라는 개념을 도입함.
-
속성(attribute) : 릴레이션 스키마의 열
-
도메인(domain) : 속성이 가질 수 있는 값의 집합
-
차수(degree) : 속성의 개수
⭐릴레이션 인스턴스: 릴레이션 스키마에 실제로 저장된 데이터의 집합
-
투플(tuple) : 릴레이션의 행
-
카디날리티(cardinality) : 투플의 수
🎨 릴레이션의 특징
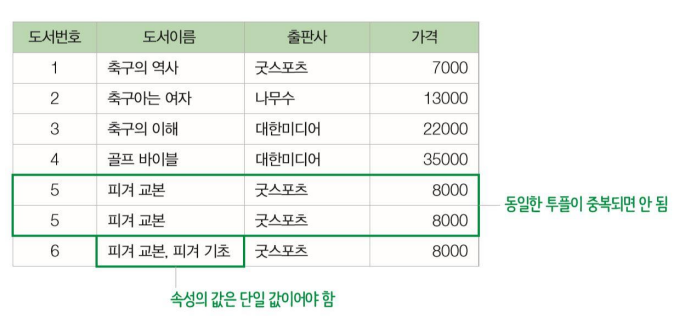
- 속성은 단일 값을 가진다
- 속성은 서로 다른 이름을 가진다
- 한 속성의 값은 모두 같은 도메인 값을 가진다
- 속성의 순서는 상관없다
- 릴레이션 내의 중복된 투플은 허용하지 않는다
- 투플의 순서는 상관없다
관계 데이터 모델
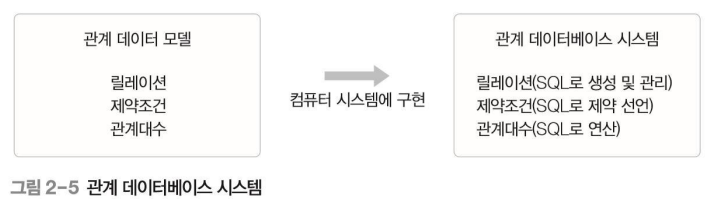
- 관계 데이터 모델은 데이터를 2차원 테이블 형태인 릴레이션으로 표현하며
릴레이션에 대한 제약조건(constraints)과 관계 연산을 위한 관계대수(relational
algebra)를 정의함.
2. 무결성 제약조건
🔥키: 특정 투플을 식별할 때 사용하는 속성 혹은 속성의 집합
-
릴레이션은 중복된 투플을 허용하지 않기 때문에 각각의 투플에 포함된 속성들 중어느 하나(혹은 하나 이상)는 값이 달라야 함. 즉 키가 되는 속성(혹은 속성의 집합)은 반드시 값이 달라서 투플들을 서로 구별할 수 있어야 함
-
키는 릴레이션 간의 관계를 맺는 데도 사용
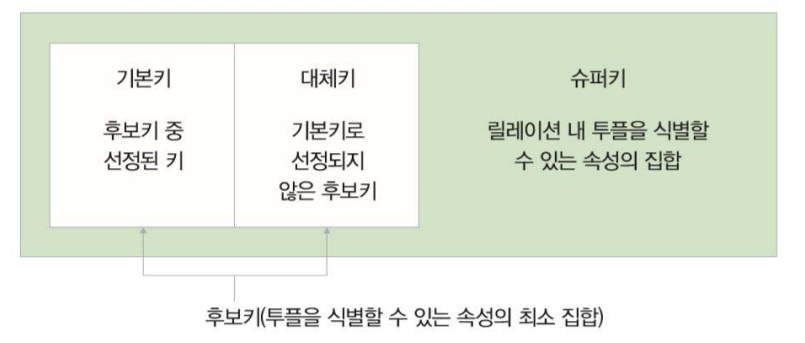
⭐슈퍼키 : 투플을 유일하게 식별할 수 있는 하나의 속성 혹은 속성의 집합
-
투플을 유일하게 식별할 수 있는 값이면 모두 슈퍼키가 될 수 있음
⭐후보키 : 투플을 유일하게 식별할 수 있는 속성의 최소 집합
⭐기본키 : 여러 후보키 중 하나를 선정하여 대표로 삼는 키
-
후보키가 하나뿐이라면 그 후보키를 기본키로 사용하면 되고 여러 개라면 릴레이션
의 특성을 반영하여 하나를 선택하면 됨.
🎨 기본키 선정 시 고려사항
▪ 릴레이션 내 투플을 식별할 수 있는 고유한 값을 가져야 함.
▪ NULL 값은 허용하지 않음.
▪ 키 값의 변동이 일어나지 않아야 함.
▪ 최대한 적은 수의 속성을 가진 것이라야 함.
▪ 향후 키를 사용하는 데 있어서 문제 발생 소지가 없어야 함.⭐대리키 : 기본키가 보안을 요하거나, 여러 개의 속성으로 구성되어 복잡하거나, 마땅한 기본키가 없을 때는 일련번호 같은 가상의 속성을 만들어 기본키로 삼는 경우가 있음. 이러한 키를 대리키(surrogate key) 혹은 인조키(artificial key)라고 함.
-
대리키는 DBMS나 관련 소프트웨어에서 임의로 생성하는 값으로 사용자가 직관적으
로 그 값의 의미를 알 수 없음
⭐대체키 : 기본키로 선정되지 않은 후보키를 말함
⭐외래키 : 다른 릴레이션의 기본키를 참조하는 속성을 말함.
- 다른 릴레이션의 기본키를 참조하여 관계 데이터 모델의 특징인 릴레이션 간의 관계(relationship)를 표현함.
- 외래키 사용 시 참조하는 릴레이션과 참조되는 릴레이션이 꼭 다른 릴레이션일 필요는 없음. 즉 자기 자신의 기본키를 참조할 수도 있음.
🎨 외래키의 특징
▪ 관계 데이터 모델의 릴레이션 간의 관계를 표현함.
▪ 다른 릴레이션의 기본키를 참조하는 속성임.
▪ 참조하고(외래키) 참조되는(기본키) 양쪽 릴레이션의 도메인은 서로 같아야 함.
▪ 참조되는(기본키) 값이 변경되면 참조하는(외래키) 값도 변경됨.
▪ NULL 값과 중복 값 등이 허용됨.
▪ 자기 자신의 기본키를 참조하는 외래키도 가능함.
▪ 외래키가 기본키의 일부가 될 수 있음.
키 – 내용 요약
🔥무결성 제약조건
데이터 무결성(integrity, 無缺性) :데이터베이스에 저장된 데이터의 일관성과 정확성을 지키는 것을 말함
💡 도메인 무결성 제약조건(도메인 제약)
• 릴레이션 내의 투플들이 각 속성의 도메인에 지정된 값만을가져야 한다는 조건
• SQL 문에서 데이터 형식(type), 널(null/not null), 기본 값(default), 체크(check) 등을 사용하여 지정할 수 있음.
💡 개체 무결성 제약조건(기본키 제약)
• 릴레이션은 기본키를 지정하고 그에 따른 무결성 원칙 즉, 기본키는 NULL 값을 가져서는 안 되며 릴레이션내에 오직 하나의 값만 존재해야 한다는 조건임.
▪ 삽입 : 기본키 값이 같으면 삽입이 금지됨.
▪ 수정 : 기본키 값이 같거나 NULL이면 수정이 금지됨.
▪ 삭제 : 특별한 확인이 필요하지 않으며 즉시 수행함.
💡 참조 무결성 제약조건(외래키 제약)
• 릴레이션 간의 참조 관계를 선언하는 제약조건
• 자식 릴레이션의 외래키는 부모 릴레이션의 기본키와 도메인이 동일해야 하며, 자식 릴레이션의 값이 변경될때 부모 릴레이션의 제약을 받는다는 것
◼ 삽입
▪ 학과(부모 릴레이션) : 새로운 투플을 삽입하면 정상적으로 진행
▪ 학생(자식 릴레이션) : 참조받는 테이블에 외래키 값이 없으면 삽입이 금지
(이런 경우 외래키에 대응하는 새로운 투플을 부모 릴레이션에 먼저 삽입한 후 수행해야 함)
◼ 삭제
▪ 학생(자식 릴레이션) : 바로 삭제 가능함.
▪ 학과(부모 릴레이션) : 참조하는 릴레이션이 있는 경우 4가지 조치를 고려할 수 있음
① 즉시 작업을 중지
② 자식 릴레이션의 관련 투플을 삭제
③ 초기에 설정된 다른 어떤 값으로 변경
④ NULL 값으로 설정
◼ 수정
▪ 삭제와 삽입 명령이 연속해서 수행되는 것으로 보면 됨.
▪ 부모 릴레이션의 수정이 일어날 경우 삭제 옵션에 따라 처리된 후 문제가 없으면 다시 삽입제약조건에 따라 처리됨.
3. 관계대수
⭐ 관계대수(relational algebra, 關係代數)
릴레이션에서 원하는 결과를 얻기 위해 수학의 대수와 같은 연산을 이용하여 질의하는 방법을 기술하는 언어
⭐ 관계대수와 관계해석
- 관계대수 : 어떤 데이터를 어떻게 찾는지에 대한 처리 절차를 명시하는 절차적인 언어이며,DBMS 내부의 처리 언어로 사용됨
- 관계해석 : 어떤 데이터를 찾는지 명시하는 선언적인 언어로 관계대수와 함께 관계 DBMS의 표준 언어인 SQL의 이론적인 기반을 제공함
→ 관계대수와 관계해석은 모두 관계 데이터 모델의 중요한 언어이며 실제 동일한 표현 능력을가지고 있음.
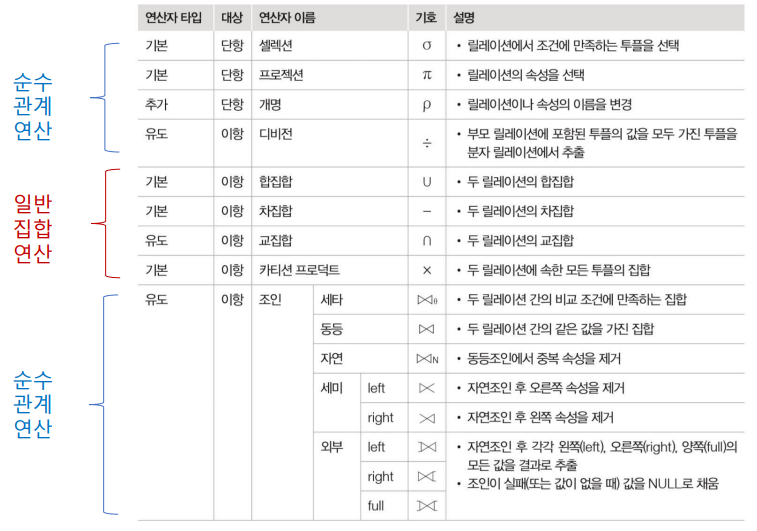
⭐관계대수식
- 관계대수는 릴레이션 간 연산을 통해 결과 릴레이션을 찾는 절차를 기술한 언어로, 이 연산을 수행하기 위한 식을 관계대수식(relational algebra expression)이라고 함.
관계대수식은 대상이 되는 릴레이션과 연산자로 구성되며, 결과는 릴레이션으로 반환됨. 반환된 릴레이션은 릴레이션의 모든 특징을 따름.
💡 릴레이션(relation)의 수학적 개념
예) A = {2, 4}, B = {1, 3, 5} 일 때
AXB = {(2,1), (2,3), (2,5), (4,1), (4,3), (4,5)} // A원소와 B원소의 순서쌍 집합
릴레이션 R은 카티전 프로덕트의 부분집합으로 정의
예) R1 = {(2,1), (4,1)}, R2={(2, 1), (2, 3), (2, 5)}, R3={(2, 3), (2, 5), (4, 3), (4, 5)}
원소 개수가 n인 집합 S의 부분집합의 개수는 2ⁿ이므로, 카티전 프로덕트 A×B의
부분집합의 개수는카티전 프로덕트의 기초 집합 A, B 각각이 가질 수 있는 값의 범위를 도메인(domain)이라고 함.
즉 집합 A의 도메인은 {2, 4}
릴레이션 역시 집합이므로 집합에서 가능한 연산은 합집합(∪), 교집합(∩), 카티전 프로덕트(×)
등이 있음.
R1 ∪ R2 = {(2, 1), (4, 1), (2, 3), (2, 5)}
R1 ∩ R2 = {(2, 1)}
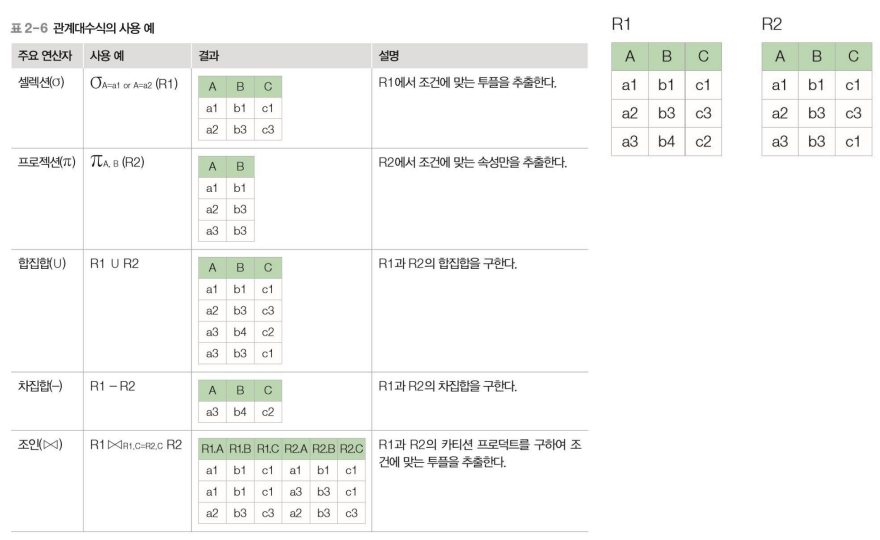
⭐관계대수식
- 관계대수는 릴레이션 간 연산을 통해 결과 릴레이션을 찾는 절차를 기술한 언어로, 이 연산을 수행하기 위한 식을 관계대수식(relational algebra expression)이라고 함.
- 관계대수식은 대상이 되는 릴레이션과 연산자로 구성되며, 결과는 릴레이션으로 반환됨. 반환된 릴레이션은 릴레이션의 모든 특징을 따름.
▪ 단항 연산자 : 연산자<조건> 릴레이션
▪ 이항 연산자 : 릴레이션1 연산자<조건> 릴레이션2
⭐셀렉션(selection)
릴레이션의 투플을 추출하기 위한 연산임. 하나의 릴레이션을 대상으로 하는 단항 연산자이며,찾고자 하는 투플의 조건(predicate)을 명시하고 그 조건에 만족하는 투플을 반환함.
◼ 형식 : σ<조건> (R) (R은 릴레이션, σ 는 그리스 문자이며 대문자는 Σ )
◼ 셀렉션의 확장
◼ 형식 : σ<복합조건> (R) (R은 릴레이션, σ 는 그리스 문자이며 대문자는 Σ )
⭐프로젝션(projection)
◼ 릴레이션의 속성을 추출하기 위한 연산으로 단항 연산자임.
◼ 형식 : π<속성리스트> (R) (R은 릴레이션, π 는 그리스 문자이며 대문자는 Π )
⭐합집합
◼ 두 개의 릴레이션을 합하여 하나의 릴레이션을 반환함. 이 때 두 개의 릴레이션은 서로 같은 속성순서와 도메인을 가져야 함. 합병가능해야함.(union compatible)
◼ 형식 : R ∪ S
⭐교집합
◼ 합병가능한 두 릴레이션을 대상으로 하며, 두 릴레이션이 공통으로 가지고 있는 투플을 반환함.
◼ 형식 : R ∩ S
⭐차집합
◼ 첫 번째 릴레이션에는 속하고 두 번째 릴레이션에는 속하지 않는 투플을 반환함.
◼ 형식 : R - S
⭐카티전 프로덕트(cartesian product)
◼ 두 릴레이션을 연결시켜 하나로 합칠 때 사용함. 결과 릴레이션은 첫 번째 릴레이션의 오른쪽에 두 번째 릴레이션의 모든 투플을 순서대로 배열하여 반환함. 결과 릴레이션의 차수는 두 릴레이션의 차수의 합이며, 카디날리티는 두 릴레이션의 카디날리티의 곱임. 두 릴레이션을 연결시켜 하나로 합칠 때 사용함.
◼ 형식 : R × S
⭐조인(join)
--> 두 릴레이션의 공통 속성을 기준으로 속성 값이 같은 투플을 수평으로 결합하는 연산임. 조인을 수행하기 위해서는 두 릴레이션의 조인에 참여하는 속성이 서로 동일한 도메인으로 구성되어야 함. 조인 연산의 결과는 공통 속성의 속성 값이 동일한 투플만을 반환함.
◼ 형식 : R C S = σc
(R×S) (R과 S는 릴레이션, c 는 조인조건)
조인 연산의 구분
▪ 기본연산 : 세타조인( ), 동등조인( ), 자연조인( )
▪ 확장된 조인 연산 : 세미조인( ), 외부조인( )
✏️ 세타조인(theta join, θ)
▪ 조인에 참여하는 두 릴레이션의 속성 값을 비교하여 조건을 만족하는 투플만 반환함.
▪ 세타조인의 조건은 {=, ≠, ≤, ≥, <, >} 중 하나가 됨.
▪ 형식 : R (r 조건 s) S (R과 S는 릴레이션이며 r은 R의 속성, s는 S의 속성)
✏️ 동등조인(equi join)
▪ 세타조인에서 = 연산자를 사용한 조인을 말함. 보통 조인 연산이라고 하면 동등조인을 지칭함.
▪ 형식 : R (r = s) S
✏️ 자연조인(natural join)
▪ 동등조인에서 조인에 참여한 속성이 두 번 나오지 않도록 두 번째 속성을 제거한 결
과를 반환함.
▪ 형식 : R N(r, s) S
✏️ 외부조인(outer join)
▪ 자연조인 시 조인에 실패한 투플을 모두 보여주되 값이 없는 대응 속성에는 NULL 값을 채워서 반환
▪ 모든 속성을 보여주는 기준 릴레이션 위치에 따라 왼쪽(left) 외부조인, 오른쪽(right) 외부조인, 완전(full) 외부조인으로 나뉨.
▪ 형식 : 왼쪽(left) 외부조인 – R (r, s) S
완전(full) 외부조인 – R (r, s) S
오른쪽(right) 외부조인 - R (r, s) S
✏️ 세미조인(semi join)
▪ 자연조인을 한 후 두 릴레이션 중 한쪽 릴레이션의 결과만 반환하며, 기호에서 닫힌 쪽 릴레이
션의 투플만 반환함.
▪ 형식 : R (r, s) S
✏️ 디비전(division)
▪ 릴레이션의 속성 값의 집합으로 연산을 수행함.
▪ 형식 : R ÷ S
