SPS LAB 2025.01.16 신입생 세미나 1주차
- 본 내용은 Michigan University의 Deep Learning for Computer Vision 3강 Linear Classifier 강의를 듣고 정리한 내용입니다.
- 강의의 원본은 해당 링크에서 확인하실 수 있습니다.
1. Parametric Approach
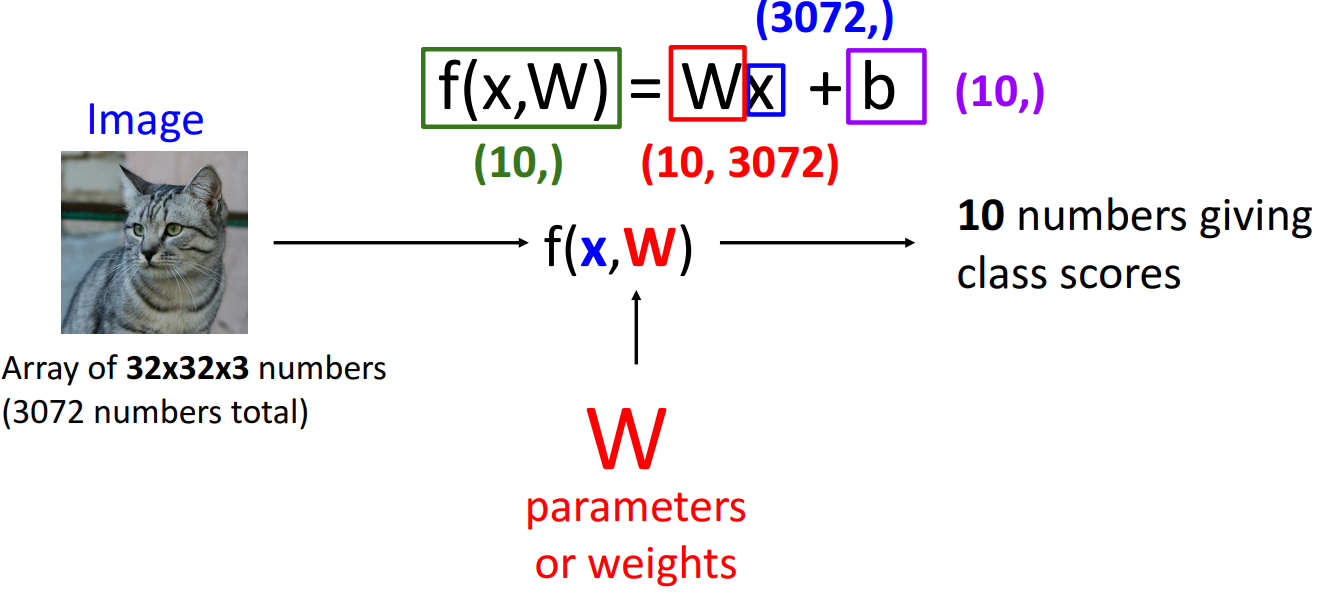
- 해석
- f(x, W): 가장 단순한 선형 분류기
- x = input data (32 x 32 x 3 array (총 3072개의 픽셀값))
- W = weight
- b = bias
- 필요한 이유: Wx만 존재할 시, 무조건 원점을 지나야 하는 문제를 해결하기 위해서
- 목표
- 10가지 클래스를 잘 분류하는 것 (각 클래스별로 score 산출하여 클래스 분류를 진행)
- 진행 방법
- input data 벡터화 (2,2) --> (4, )

- weight, bias 적용하여 f(x,W) 값 구하기
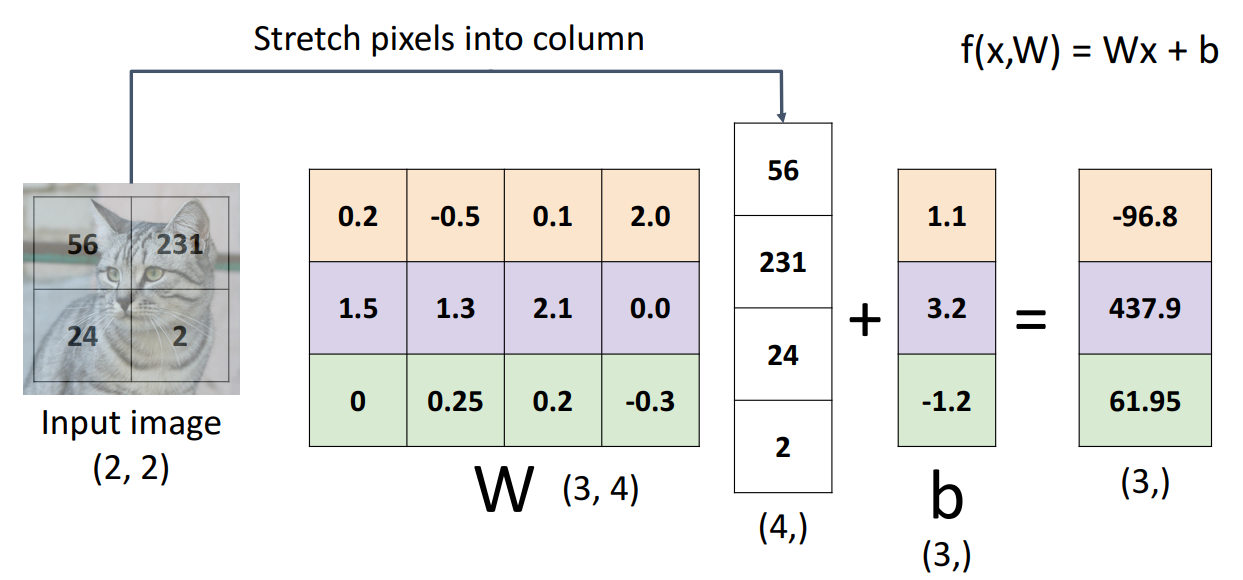
- input data 벡터화 (2,2) --> (4, )
2. Linear Classifier: Three Viewpoints
1. Algebraic Viewpoint
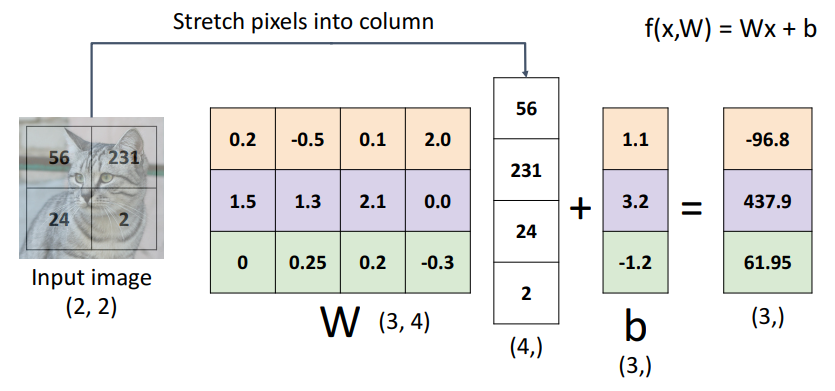
- input data를 벡터화하고, 행렬 내적 계산하는 대수적 관점
- bias가 없는 경우에는 상수 c에 따라 선형적으로 예측 결과가 도출

2. Visual Viewpoint

- weight를 input data와 동일한 형태로 만들어 계산을 진행하는 시각적 관점
- 각 카테고리별로 template가 1개가 존재하고, single template는 data의 multiple modes를 포착할 수 없음

3. Geometric Viewpoint
- 선형 분류기의 출력 점수는 클래스 간의 선형 경계로 정의되며, 각 클래스는 고유한 점수 공간을 가져 입력 데이터가 이 공간에서 어디에 위치하는지에 따라 클래스를 예측
- 빨간색, 파란색, 녹색 선은 결정 경계(hyperplane)을 나타내며, 이를 활용하여 각 데이터 포인트가 속할 클래스를 예측
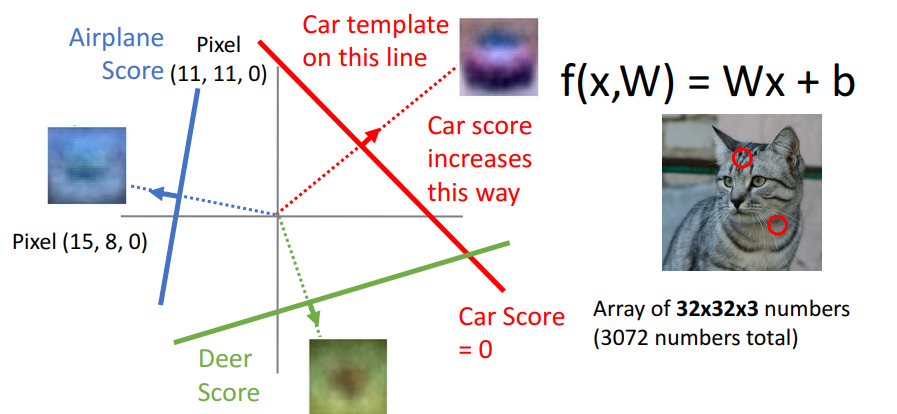
3. Loss function
- 정의
- 좋은 분류기인지 판단하는 지표로, objective function, cost function이라고도 불림
- loss가 낮을수록 good classifer이고, 높을수록 bad classifier임
- Negative loss function은 반대로 높을수록 성능이 좋은 classifier이고, reward function, profit function, utility function, fitness function이라고 불림
- 다양한 종류의 Loss function이 존재하며, 각 task마다 적합한 Loss function을 설정해줘야 좋은 결과를 얻을 수 있음
- 수식
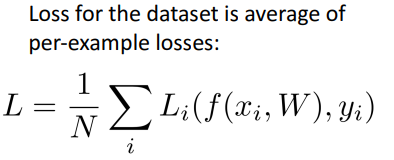
4. Loss function의 종류
1. Multiclass SVM Loss
-
정의

- 모델은 정상 클래스의 score가 다른 모든 클래스의 점수보다 더 높아야 한다
- Multiclass SVM Loss는 정답 클래스 점수가 다른 클래스의 점수보다 충분히 높도록 모델을 학습시켜야 한다
-
수식

- 잘못된 클래스의 점수(s_j)를 정답 클래스의 점수(s_y_i)보다 낮게 유지하면서 마진 Δ 이상을 확보하려는 것
- 정답 클래스 >= 오답 클래스 + 1(margin)이면 loss는 0임
-
예시

2. Cross Entropy Loss
- 정의
- 분류 문제에서 모델이 예측한 확률 분포와 실제 정답 분포 간의 차이를 계산하는 데 사용
- 수행 단계

- Unnormalized Log-Probabilities (Logits)
- 모델의 출력 s는 정규화되지 않은 logit 값으로, 각 클래스에 대한 점수를 나타냄
ex) cat = 3.2, dog = 5.1, frog = -1.7
- 모델의 출력 s는 정규화되지 않은 logit 값으로, 각 클래스에 대한 점수를 나타냄
- Exponentiation
- logit 값을 지수 함수(exp)를 통해 변환
ex) e^3.2 = 24.5, e^5.1 = -164.0, e^-1.7 = -0.18
- logit 값을 지수 함수(exp)를 통해 변환
- Normalization (Softmax Function)
- Softmax 함수를 사용하여 각 클래스의 값을 확률 분포로 변환
- 이 확률은 모든 클래스의 합이 1이 되며, 각 클래스에 대한 모델의 신뢰도를 나타냄

- Loss 계산
- 정답 클래스의 확률을 모델의 출력 확률 분포에서 추출하고, 이 확률값에 로그를 적용하여 음수로 변환한 후 손실로 사용
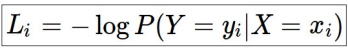
- 정답 클래스의 확률을 모델의 출력 확률 분포에서 추출하고, 이 확률값에 로그를 적용하여 음수로 변환한 후 손실로 사용
- Cross Entropy 계산
- 모델의 출력 확률 분포 Q와 실제 정답 분포 P 간의 차이를 측정
- 두 분포가 완전히 같으면 0이 되고, 다를수록 커짐
- 정답 분포 P = [1, 0, 0] / 모델 출력 Q = [0.13, 0.87, 0]
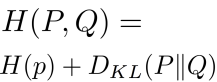
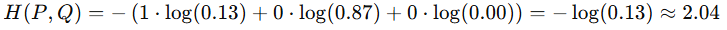
- Unnormalized Log-Probabilities (Logits)
3. SVM Loss와 Cross Entropy Loss 차이점
- SVM Loss
- 단순히 클래스 점수 간의 차이를 기반으로 학습하여 예측된 점수에 대한 확률 해석 제공하지 않음
- Cross entropy Loss
- Softmax 함수를 사용하여 모델 출력을 확률로 변환하기 때문에 예측 점수에 대한 확률적 해석 제공
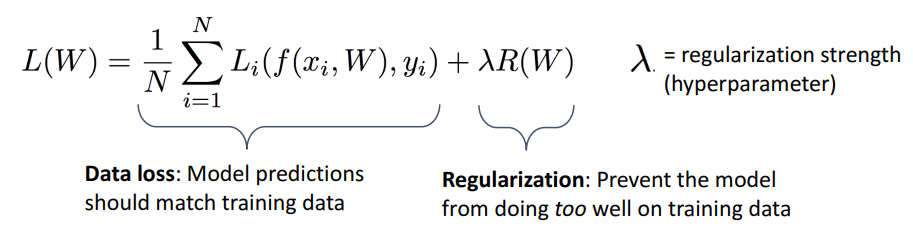
5 . Regularization
-
정의
- 모델이 훈련 데이터에서 너무 잘 작동하지 않도록 방지
-
목적
-
training error 최소화를 넘어 모델 간 선호도(preferences) 표현
- loss 함수에 regularization 항 추가하면 더 선호하는 weight 표현 가능
ex) L2 Regulatization은 weight가 퍼져 있는 것을 선호

- loss 함수에 regularization 항 추가하면 더 선호하는 weight 표현 가능
-
overfitting 방지: 더 잘 일반화되는 간단한 모델 선호
- f1: training data를 완벽하게 fit
- f2: training error가 존재하지만, simple

-
곡률(curvature) 추가하여 optimization 개선
-
