반갑습니다.

알고리즘 수업 듣는 윤강훈입니다.

강의자료 보면서 정리 한 번 하고, 강의 자료에다가 정리 한 번 했으니 이제 이해한 거 바탕으로 프리스타일로 정리하러 왔습니다.

Desirable Characteristics of an Algorithm

일단 바람직한 알고리즘의 특성들 간단하게 짚고 가자.

1. Efficiency(효율성): 가능한 빠르고, 가능한 적은 메모리를 써야한다.
2. Simplicity(단순성): 이해하고 구현하기 쉬워야한다.
3. Generality(일반성): 일반적인 문제와 입력에 대해 작동해야한다.
4. Optimality(최적성): 다른 알고리즘에 비해 제일 좋은 성능이어야한다.

시험에 간단하게 나올 법 하니 ESGO 로 외워두도록 하자.

Efficiency

우리는 저 4개 중 Efficiency에 초점을 맞춘다.

그 중에서도 run time, 즉 실행 시간에 좀 더 초점을 맞춰보자.

Asymptotic Analysis

하지만 그렇다고 하나 하나 다 따질 건 아니다.

세세하게 따지면 컴퓨터의 성능이라던가, 어떤 언어를 사용하냐에 따라서 까지 달라질 수 있기 때문이다.

말 빠른 사람이 빠르게 말한다고 문장의 길이가 줄어드는 건 아닌거랑 같다.

알고리즘 실행 시간은 Input Size, $n$ 에 의해 결정된다.

어떤 다른 요인이 있어도 input으로 1000억개가 들어오면 무의미해진다.

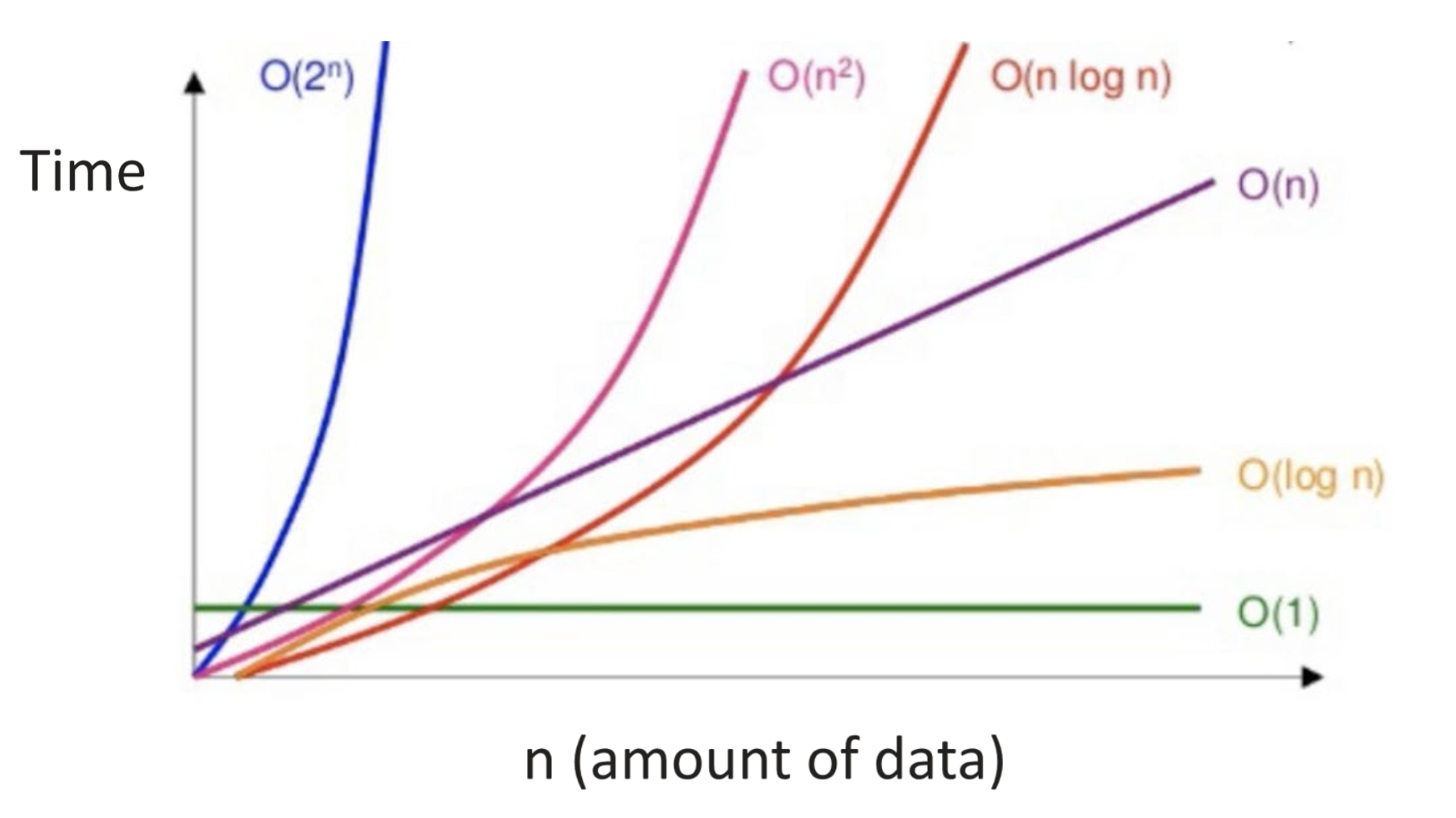
그래프를 보면 확 와 닿을 것이다, n이 커질 수록 시간에 좀 더 유의미한 결과를 보인다.

여기서 하나의 조건이 더 추가된다.

최고차항을 기준으로 생각하자.

이 말이 뭐냐면

$f_1(x) = x^2$과

$f_2(x) = 1.1x^2 + (x^{1.9}+10)sin(10x+1.5) +30$

을 서로 같은 걸로 간주한다는 것이다.

그냥 그런갑다 하면 된다.

그게 룰이니까.

Big-O Notation

이제 표기법에 대해서 좀 알아보자.

가장 유명한 Big-O Notation 이 있다.

사실 이것만 알고나면 Big-Omega나 Big-Theta도 같은 맥락이니까 잘 알고 가자.

Big-O는 함수 성장 속도의 상한을 나타낸다.

이 말이 되게 모호하게 들릴 수 있는데, 알고리즘의 시간이 이것보다 더 느릴 수는 없다는 것이다.

예를 들어 어떤 한 알고리즘이 $O(n^2)$으로 표기된다면, $T(n)$의 최고차항이 $n^2$보다 클 수 없다는 것이다.

$T(n) = log(n)$ 인 건 괜찮냐고?

물론 상관없다.

말 그대로 상한을 나타내는 것이기 때문에 저것보다 작은 것들은 정말 알빠가 아니다.

정말 꼴 보기 싫지만 수식으로 한 번 나타내보자.

$O(g(n)) = \{T(n) | \exists c>0, n_0>0 s.t. \forall n\geq n_0, T(n) \leq c\times g(n)\}$

즉,

모든 $n\geq n_0$에 대하여 $T(n) \leq c\times g(n)$인 양의 상수 $c$와 $n_0$가 존재한다.

라는 의미이다.

그냥 뭐 $g(n)$에 특정한 상수를 곱해서 $T(n)$보다 큰 경우가 생기면 성립한다고 생각하면 편할 듯 하다.

Big-Omega Notation

이 친구는 상한이 아니라 하한을 나타낸다.

특정 알고리즘이 이것보다 더 빠를 수 없다는 것이다.

만약 $\Omega(n)$이라면 $T(n)$의 최고차항이 $n$보다 작을 수 없다.

수식 한 번 더 가자.

근데 그냥 Big-O의 반대다.

$\Omega(g(n)) = \{T(n) | \exists c>0, n_0>0 s.t. \forall n\geq n_0, T(n) \geq c\times g(n)\}$

즉,

모든 $n\geq n_0$에 대하여 $T(n) \geq c\times g(n)$인 양의 상수 $c$와 $n_0$가 존재한다.

라는 의미이다.

Big-Theta Notation

이 친구는 위의 두 조건을 모두 만족하는 경우를 나타낸다.

어떻게 보면 조금 정확하게 나타내준다고 볼 수도 있겠다.

$T(n)=O(g(n))$ 이고, $T(n)=\Omega(g(n))$ 일 때, $T(n)=\Theta(g(n))$이다.

이것도 수식 한 번 조져주자.

둘이 합쳐주면 그만이다.

$\Theta(g(n)) = \{T(n) | \exists c_1, c_2>0, n_0>0 s.t. \forall n\geq n_0, c_1\times g(n) \leq T(n) \leq c_2\times g(n)\}$

즉,

모든 $n\geq n_0$에 대하여 $c_1\times g(n) \leq T(n) \leq c_2\times g(n)$인 양의 상수 $c_1, c_2$와 $n_0$가 존재한다.

아무튼 이렇게 다 알아보았다.

Define

앞으로 알고리즘에 대해 생각할 때 우리는 최악의 경우에 초점을 맞춘다.

그 말은 더 나은 알고리즘이라는 것이 최악의 경우에서 최선의 성능을 내는 알고리즘 이라는 것이다.

최선의 경우에서는 어느 알고리즘이나 최선의 결론을 도출해낸다.

이미 정렬되어 있는 리스트에서 정렬을 시키면 누가 못하겠냐는 것이다.

입력 사이즈가 클 때, 역순으로 정렬되어 있는 리스트에서의 성능을 체크하는 것이 가장 바람직하다.