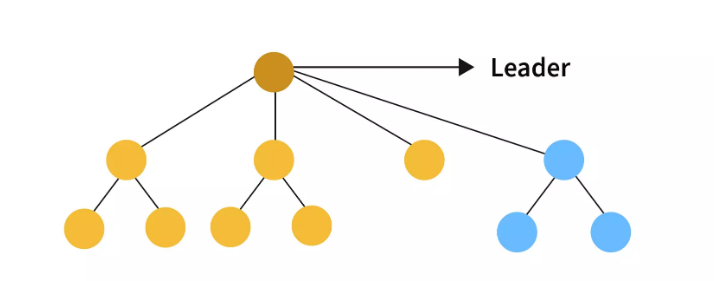
서로소 집합(disjoint-set) 자료 구조, 또는 합집합-찾기(union–find) 자료 구조, 병합-찾기 집합(merge–find set)은 많은 서로소 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료 구조이다.
서로소 집합 자료 구조는 MakeSet, Union, Find 세 개의 유용한 연산을 제공하고 이 세 연산을 활용하여 많은 파티션(partitioning) 문제들을 해결 할 수 있다.
연산
Make-Set
특정 한 원소만을 가지는 집합을 만든다.
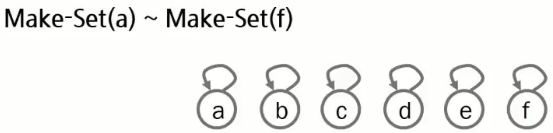
Union
두 개의 집합을 하나의 집합으로 합친다.
- 연산의 효율을 높이기 위해 트리의 높이(rank)가 낮은 집합을 높이가 높은 집합에 붙인다.
- 트리의 높이가 높아질수록 Find연산이 오래 걸린다.
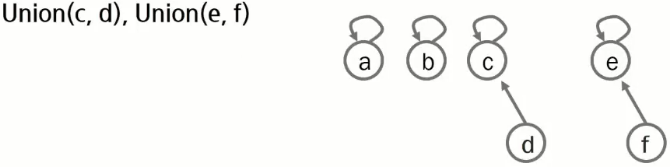
Find
어떤 원소가 주어졌을 때 이 원소가 속한 집합을 반환한다. 파인드는 일반적으로 어떤 원소가 속한 집합을 "대표" 하는 원소를 반환하는데, 이를 위하여 어떤 원소와 각 대표 원소들 간의 파인드 결과를 비교하여 같은 집합임을 판단한다.
- Path Compression 기법으로 효율을 높일 수 있다.

표현
서로소 집합 데이터 구조는 간단히 각 집합을 표현하기 위하여 연결리스트 또는 트리를 사용한다.
트리의 경우 각 노드들은 부모 노드를 참조하고 각 집합의 대표는 해당 트리의 루트(root) 노드이다. 파인드 연산은 특정 노드에서 루트 노드에 도달할 때까지 부모 노드를 따라 참조한다. 유니온은 두 개의 트리를 하나로 병합하는 연산으로 한 루트 노드를 다른 루트 노드에 연결한다.
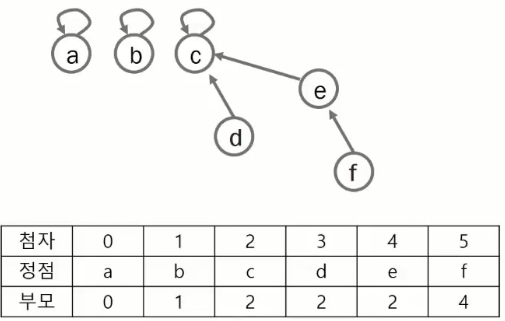
- 하나의 집합(a disjoint set)을 하나의 트리로 표현
- 자식 노드가 부모 노드를 가리킨다.
- 루트 노드는 자기 자신을 가리키며 루트 노드가 대표자가 된다.
구현
def make_set(x):
parent[x] = x
rank[x] = 0
def find(x):
if parent[x] != x:
# Path Compression 기법으로 루트노드를 가리키도록해서 연산의 속도를 높인다.
parent[x] = find(parent[x])
return parent[x]
def union(a, b):
a = find(a)
b = find(b)
# 높이가 낮은 집합을 높은 집합 밑으로 합쳐서 높이가 높아지는 것을 방지해 연산의 효율을 높인다.
if rank[a] > rank[b]:
parent[b] = a
else:
parent[a] = b
# 높이(rank)가 같은 집합을 합치면 총 높이가 1증가한다.
if rank[a] == rank[b]:
rank[b] += 1응용
두 개의 노드(vertex)들이 같은 집합에 속하는지 또는 그 노드들을 간선(edge)으로 연결 할 때 싸이클(cycle)이 발생하는지 등을 확인 할 수 있다. 이를 활용해 쿠르스칼(Kruskal) 알고리즘에서 그래프의 최소 신장 트리(minimum spanning tree)를 찾는데 활용된다.
- 최소 신장 트리(MST)
- 그래프에서 최소 비용 문제
- 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리
- 신장 트리
- n개의 정접으로 이루어진 무방향 그래프에서 n개의 정점과 최대 n-1개의 간선으로 이루어진 트리
KRUSKAL 알고리즘
- 모든 간선을 가중치에 따라 오름차순으로 정렬
- 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킴
- 사이클이 존재하면 다음 가중치가 낮은 간선 선택
- n-1개의 간선이 선택될 때 까지 반복
for u, v in range(e):
if find(u) != find(v):
union(u,v)