힙(heap)

• 영단어 힙(heap)은 '무엇인가를 차곡차곡 쌓아올린 더미'라는 뜻을 지니고 있다.
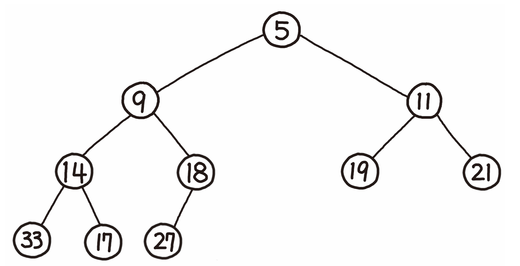
• 힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(complete binary tree)를 기본으로 한 자료구조이다.
• A가 B의 부모노드(parent node) 이면, A의 키(key)값과 B의 키값 사이에는 대소관계가 성립한다.

따라서 루트노드에는 항상 데이터들 중 가장 큰 값(혹은 가장 작은 값)이 저장되어 있기 때문에, 최댓값(혹은 최솟값)을 O(1)안에 찾을 수 있다.

종류

힙에는 두가지 종류가 있다.

• 최대 힙(max heap): 부모노드의 키값이 자식노드의 키값보다 항상 큰 힙
• 최소 힙(min heap): 부모노드의 키값이 자식노드의 키값보다 항상 작은 힙

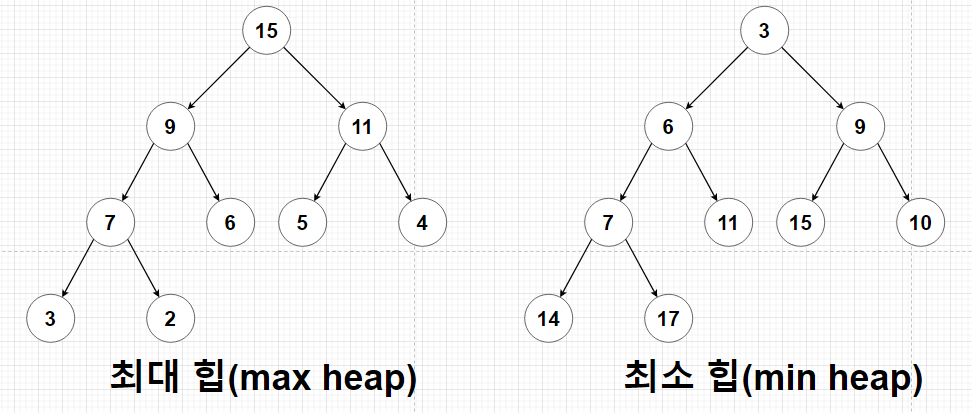
키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 특히 형제 사이에는 대소관계가 정해지지 않는다.

연산

데이터의 삽입과 삭제는 모두 O(logN)이 소요된다.

데이터 삽입

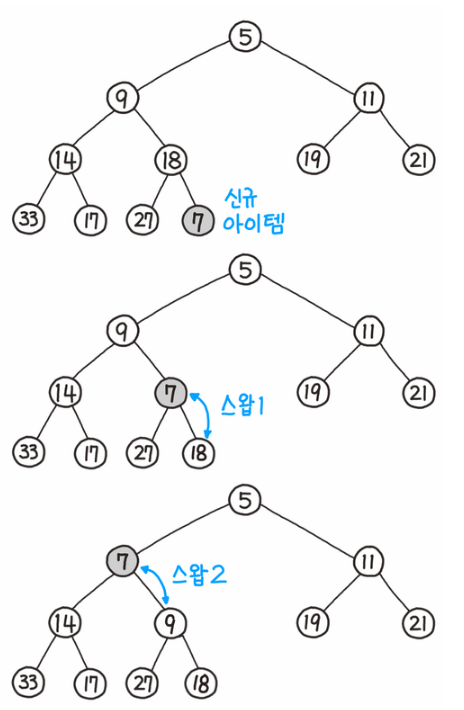
1. 가장 끝의 자리(가장 하위 레벨의 최대한 왼쪽)에 노드를 삽입한다.
2. 부모 값과 비교해 값이 더 작은 경우(최대 힙의 경우 더 큰 경우) 위치를 변경한다.
3. 계속해서 부모 값과 비교해 위치를 변경한다.

데이터 삭제(추출)

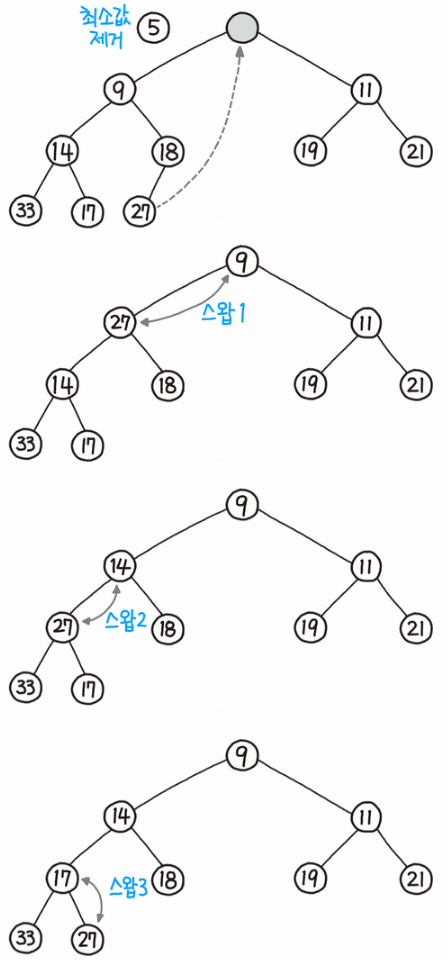
1. 루트노드를 제거(추출)한다.
2. 루트 자리에 가장 마지막 노드를 삽입한다.
3. 자식 노드들과 값을 비교해서 자식보다 크다면(최대 힙의 경우 작다면) 위치를 변경한다.
4. 계속해서 자식과 값을 비교해 위치를 변경한다.

표현

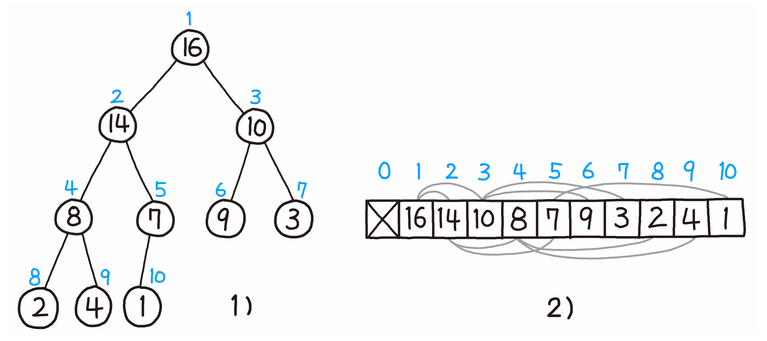
이진 힙은 완전 이진 트리(Complete Binary Tree)로서, 배열로 표현하기 매우 좋은 구조로 빈틈없이 배치가 가능하다.
대개 트리의 배열 표현의 경우 계산을 편하게 하기 위해 인덱스는 1부터 사용한다.

• 부모 노드: i//2
• 왼쪽 자식 노드: 2i
• 오른쪽 자식 노드: 2i+1

응용

힙에서는 가장 높은(혹은 가장 낮은) 우선순위를 가지는 노드가 항상 뿌리노드에 오게 되는 특징을 이용해 우선순위 큐와 같은 추상적 자료형을 구현할 수 있다.

다익스트라 알고리즘에도 활용된다. 힙 덕분에 다익스트라 알고리즘의 시간 복잡도는 O(V^2)에서 O(ElogV)로 줄어들 수 있었다.

힙 정렬, 최소 신장 트리(MST)를 구현하는 프림 알고리즘에도 활용된다.

참고

https://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
https://namu.wiki/w/%ED%9E%99%20%ED%8A%B8%EB%A6%AC