해당 포스트에 쓰인 모든 이미지의 출처는 코드스테이츠입니다.
주제
- 시간복잡도가 무엇이고 왜 사용되는지?
- 각 자료구조별 시간복잡도 분석
1. Complexity Analysis - 복잡도 분석
- input n 에 대하여 알고리즘이 문제를 해결하는 데에 얼마나 오랜 시간이 걸리는 지를 분석하는 것
- Big-O 표기를 이용하여 정의할 수 있다.
- O(1) – 상수 시간 : 입력값 n 이 주어졌을 때, 알고리즘이 문제를 해결하는데 오직 한 단계만 거친다.
- O(log n) – 로그 시간 : 입력값 n 이 주어졌을 때, 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다.
- O(n) – 직선적 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가진다.
- O(n^2) – 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱이다.
- O(C^n) – 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱이다.
왜 중요한가?
- 자료구조 메소드들의 시간복잡도가 무엇인지 생각을 하면서 상황에 더 맞는 답인지 아닌지를 알고 사용하는 것이 중요하다.
- 각각의 데이터구조 장, 단점을 알아야 데이터구조를 효율적으로 사용할 수 있다.
- 문제를 해결하려고 할 때마다 시간복잡도를 분석하는 습관을 들이는 것이 중요하다.
시간복잡도 예제
숫자의 배열에서 두 수의 차가 가장 큰 것을 찾는 문제
1. 모든 경우의 수를 확인하는 방법 - n² => O(n²)
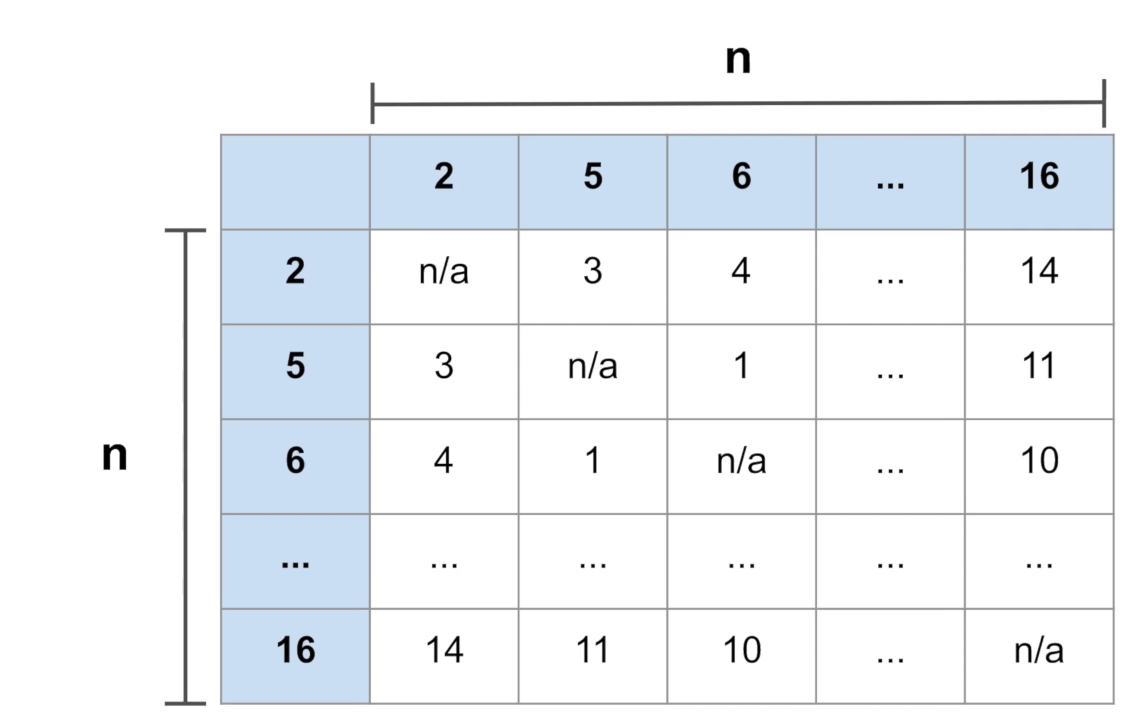
2. 가장 큰 수와 작은 수를 확인하는 방법 - 2n => O(n)
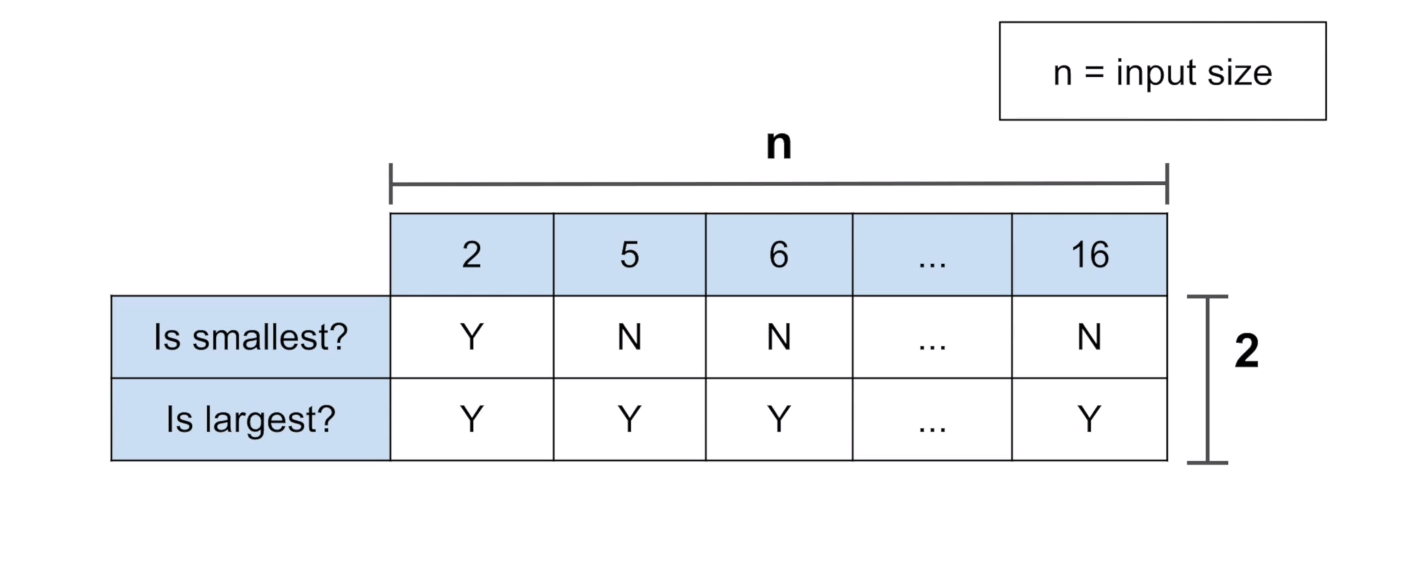
3. 값이 정렬된 경우일 때 (오름차순일 경우) - 3 => O(1)
- 최고로 빠른 시간 복잡도를 가진다.
- 가장 큰 수에서 가장 작은 수를 빼면 된다
- 숫자의 개수와 상관없이 항상 3번 계산
1. 맨 앞에 숫자를 뽑고- 맨 뒤의 숫자를 뽑고
- 두개의 숫자를 빼준다
요약 - Big-O Notation
1. constant : O(1)
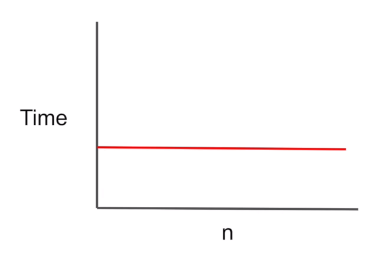
- 문제의 크기가 커져도 걸리는 시간은 항상 일정하다.
- 값을 검색할 때, 객체에서 키를 알거나 배열에서 인덱스를 알고 있으면 언제나 한 단계만 걸린다.
- ex) 배열에서 특정 인덱스 탐색, 해시테이블에서 추가
2. logarithmic : O(log n)
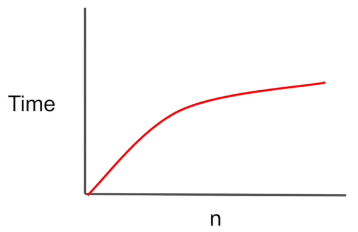
- 배열에서 값을 찾을 때, 어느 쪽에서 시작할지를 알고 있으면 검색하는 시간이 두배로 준다.
- ex) 이진탐색트리
3. linear : O(n)
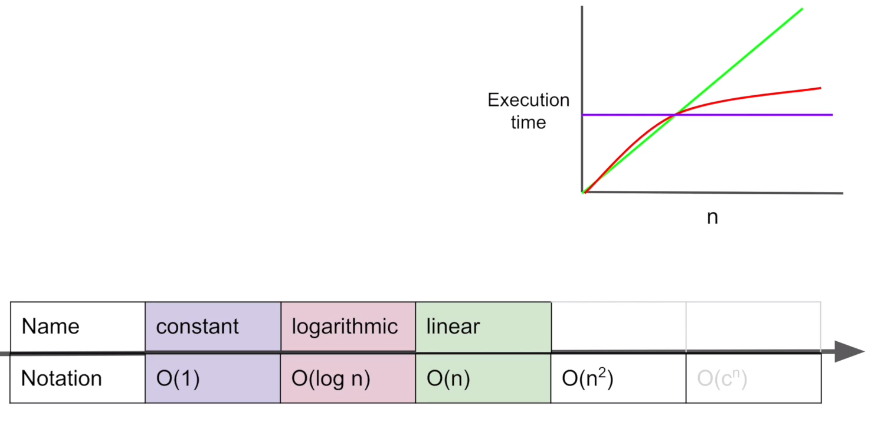
- 데이터의 갯수만큼 탐색할 경우
- linked list, Array 탐색
4. quadratic : O(n^2)
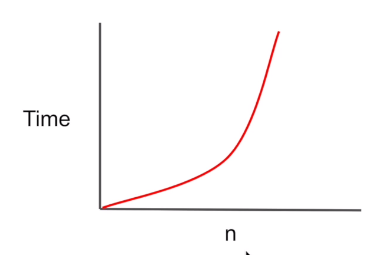
- 문제를 풀기 위해 모든 조합과 방법을 시도할 때 사용된다.
- for문 안에 for문
5. esponential : O(c^n)
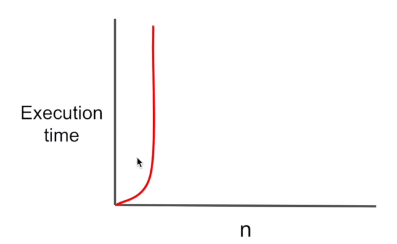
- recursion에서 memoiz기법을 사용하지 않았을때
Data structure With Time Complexity
Array, linked list, Trees의 Time Complexity
1. Arrays
- 값 조회(Lookup, index 사용) => O(1)
- 값 할당(Assignment) => O(1)
- 값 추가(insert) => O(n)
- 추가한 값의 뒤에 위치하는 값들을 모두 뒤로 당겨줘야한다.
- 값 삭제(remove) => O(n)
- 삭제한 값의 뒤에 위치하는 값들을 모두 앞으로 당겨줘야한다.
- 값 조회(Find, value 사용) => O(n)
- 모든 값들을 돌면서 찾고있는 값과 동일한지 비교해야한다.
2. Linked List
- 값 조회(Lookup, index 사용) => O(n)
- 값 할당(Assignment) => O(n)
- head부터 시작해서 해당 index까지 count를 해주어야 한다.
- 값 조회(Find, value 사용) => O(n)
- head부터 시작해서 찾는 value가 나올때 까지 비교해야 한다.
- 값 추가(insert) => O(1)
- 값 삭제(remove)
- head => O(1)
- middle => O(n)
- 삭제하려는 값의 이전값을 모르기때문에 삭제하려는 값이 next로 담긴 값까지 탐색해야함
- 단, 이전값(prev)를 참조하는 Doubly-Linked-Lists를 사용하면 복잡도는 O(1)이다.
- Doubly-Linked-Lists가 Linked-Lists보다 참조하는 주소값이 많으므로 메모리는 더 많이 차지한다.
3. Tree
Root Node => children
- 값 조회(Find, value 사용) => O(n)
- 값 할당(Assignment) => O(n)
- 값 추가(insert) => O(1)
- 값 삭제(remove)
4. Binary Search Tree
Root Node => children => Left (OR) Right
- 값 조회(Find, value 사용) => O(log n)
❗ 예외 케이스 ❗
한쪽으로만 값이 몰릴 경우 => O(n)
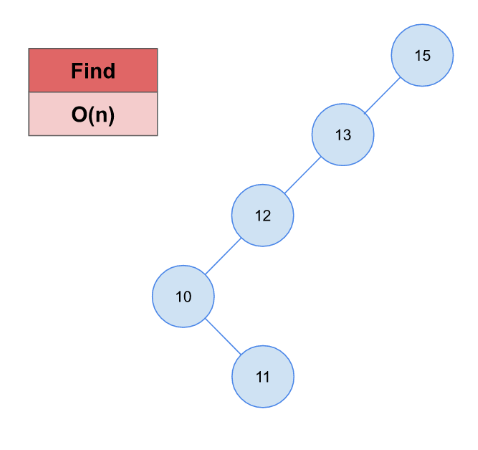
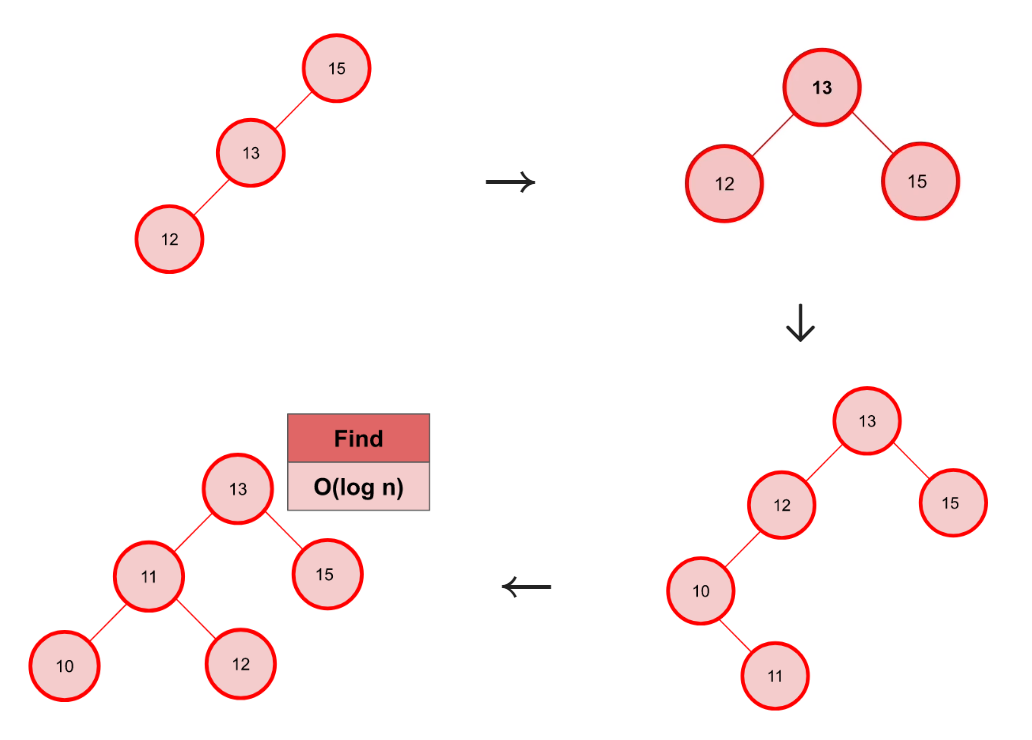
[ 위의 경우를 방지하기 위한 Solution ]
1. 각 Parents의 왼쪽, 오른쪽 가지들의 깊이가 1을 초과하여 차이가 난다면 밸런스가 무너진 상태
2. 밸런스가 무너질 때 마다 가지의 깊이가 더 깊은 쪽의 값을 얕은 쪽으로 이동시킨다.
3. 이렇게 하면 트리의 복잡도는 항상 O(log n)
정렬된 배열 vs 이진탐색트리
Array는 연속된 공간을 차지하지만,
Tree를 Linked List를 사용하여 구성하게 되면 공간을 연속적으로 차지하지 않고 메모리 구석구석에 위치할 수 있어서 메모리를 효율적으로 사용할 수 있다.
💁♀️ 참고블로그
