1. 단속 카메라

의외로 간단한 문제이다. 각 차량들의 진입 시점과 진출 시점이 담긴 array를 받자. 그리고 가장 차량이 많이 지나다니는 시점에 단속카메라를 설치해야하고, 모든 차량이 한번은 단속카메라의 범위에 들어와야한다고 하자. 이때, 설치되는 총 카메라 수를 리턴하면 된다.

예를 들어서 아래와 같이 정보가 주어진다고 하자.

[
  [-20, -15],
  [-14, -5],
  [-18, -13],
  [-5, -3],
]; // 2

첫 번째 차량은 -20에 들어와서 -15에 나간다고 보면 된다. 이걸 그림으로 보면서 최적의 카메라 위치를 찾아보자.

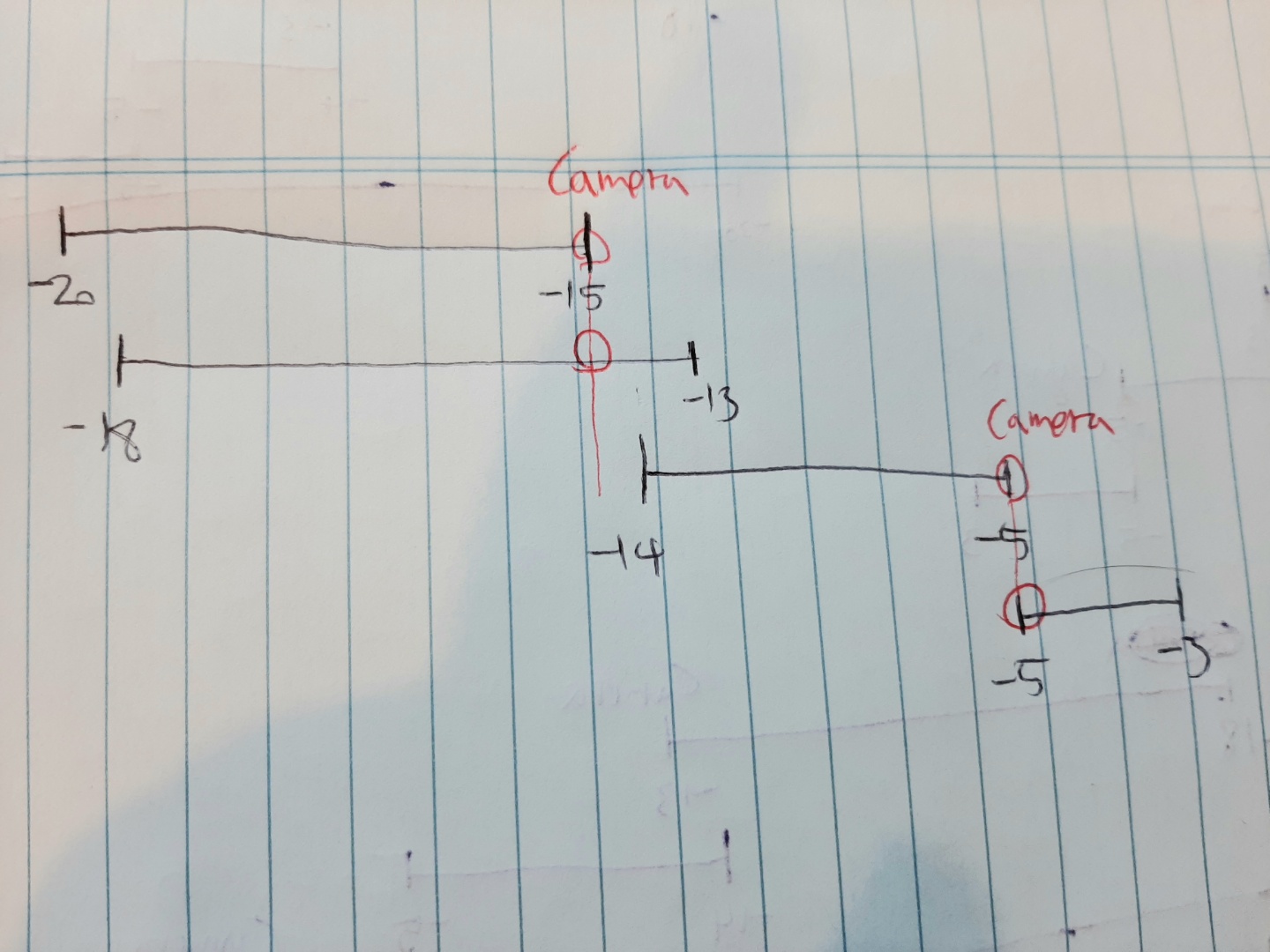
우선 진출 순서가 가장 빠른것부터 나열한다고 했을때 -15 시점에 한 대 -5에 한 대 그래서 총 2대를 설치하면 가장 효율적으로 배치한것이 되어버린다. -15시점에 설치된 카메라는 첫번째와 세번째 차량을 찍게 되고, -5 카메라는 두번째와 네번째 차량을 찍게 된다.

그럼 코드를 구현해보자.

2. 접근 방법

• pseudo code
  • 우선 진출을 기준삼아 오름차순으로 정렬하자.
    • 진출 시점으로 해야 카메라에 걸리기 때문이다.
    • 진입 시점으로 한다면 진출이 카메라 설치 시점보다 적을 수 있다. 그럼 카메라에 안걸린다.
  • 첫번째 카메라를 -30001지점에 설치함
  • for 문을 돌린다
    • 첫번째 카메라보다 진입지점이 나중이라면 진출지점에 카메라를 설치한다.
    • 왜냐하면 진출지점에 설치해야 카메라가 커버 가능한 범위가 최대가 되기 때문.

function solution(times) {
  let answer = 0;
  times.sort((a, b) => a[1] - b[1]);
  let camera = -30001;

  for (let i = 0; i < times.length; i++) {
    // 카메라가 진입 지점보다 전에 있으면 answer를 해줌
    // 그리고 카메라의 위치를 진출지점에 재배치

    // 차량 진입지점 전에 카메라가 있다는 것은 무슨의미냐?

    // 내가 그 카메라에 안 걸린다는 뜻이다.
    // 그래서 그때 새로운 카메라를 진출지점에 설치하면 된다.

    // 왜 진출 지점인가?
    // 진입지점에 설치하면 커버가능한 카메라의 범위가 줄어들기 때문이다.
    // 예를 들어서, [-14,-5] 차량이 이전 카메라(-15의 위치에 설치됨)의 범위를 벗어났다고 하자.
    // 이때, 새로운 카메라를 -14위치에 달면 다시 -14이후에 진입한 차량은 카메라의 영향을 안받기 때문에
    // 최적의 위치라고 할 수 없다. 그리고 이때 카메라가 커버가능한 범위는 -15 ~ -14로 고작 1의 범위이다.

    // 그러나 -5 지점에 카메라를 달면  카메라가 커버가능한 범위가 넓어진다.
    // 카메라의 범위가 -15 ~ -5로 늘어나는 것이다.

    // 진출지점에 카메라를 달면 그 다음 차량을 잡아낼 수 있는 확률이 높아진다고 보면된다.

    // 카메라가 진입지점 보다 뒤에 있다는 것은 무슨의미냐?
    // 내가 그 카메라에 걸린다는 뜻이다.
    // 그래서 그때는 그냥 반복문에서 지나가면 된다. 굳이 카메라를 머 설치하고 그럴필요없다.

    if (camera < times[i][0]  ==> 차량 진입 시점) {
      camera = times[i][1] ==> 차량 진출 시점;
      answer++;
    }
  }
  return answer;
}

간단한 문제였다. 이러한 로직을 어떻게 생각해 낼 수 있을까? 역시 그림을 그려보고 카메라의 위치가 어디쯤에 있으면 가장 좋을지 임시로 그려본다. 그리고 반복문에서 어떻게 코드를 짜면 카메라가 가장 최적의 위치에 선정이 될지 고민해본다.

그림상으로는 카메라보다 더 이전에 진입한 차량들은 그냥 통과해도 된다. 카메라 보다 이후에 진입한 차량일때 뭔가 조치가 이루어져야 한다. 다음 카메라의 위치를 선정하는 일이다. 다음카메라의 위치는 바로 진출위치에 설정하는 것이다.

시각화하고 쉽게쉽게 차근차근 생각해봐라. 그럼 실마리가 잡힌다.