
1. 변장술!
옷의 종류와 옷이 주어지면 그 옷을 가지고 얼마나 많은 경우의 수를 뽑아낼 수 있는지 물어보는 문제이다. 예를들어, 다음과 같은 옷이 주어졌다고 해보자.
let clothes = [
["yellowhat", "headgear"],
["blackhat", "headgear"],
["yellowsunglasses", "eyewear"],
["green_turban", "headgear"],
["yellowsunglasses", "eyewear"],
["sandle", "shoes"],
["sandle", "shoes"],
["orange_turban", "headgear"],
["sandle", "shoes"],
["bluesunglasses", "eyewear"],
["sandle", "shoes"],
["sandle", "shoes"],
];여기서 모자와 안경과 신발을 하나만 바꾸어도 변장에 성공하는 거다. 그러니깐 yellow hat + green_turban + sandle을 입었다가 다음날 bluesunglasses로 바꾸면 변장에 성공하는 것이다.
2. 접근 방법
이건 우선 각 종류의 옷을 key로 두고 거기에 해당하는 옷의 갯수를 value로 두는 hash를 먼저 만들어야 한다. 그러고 나서 옷의 종류의 경우의 수를 구한다음에 (신발/모자 or 신발/안경 ...) key에 해당하는 value를 곱해서 더하면 된다. 즉 일단 옷 종류에 대한 부분집합을 만든뒤에 그 집합에 해당되는 value를 곱해서 더하자! 저번에 부분집합을 만들어 봤으니 그걸 적용해서 풀어보자.
- pesudo code
- clothesHash를 만든다
- clothesHash로 closet array를 만든다
- checkArr를 만든다
- subset 함수를 만들고 checkArr를 이용해서 부분집합을 만든다
- 부분집합에 해당되는 옷종류의 갯수를 곱하고 곱한 값을 누적해서 더해나간다.
- 다만 아무것도 안입는 경우도 있으니 그 경우는 제외하기 위해 caculate boolean을 사용한다
function mySolution(clothese) {
// setting
let clothesHash = [];
let closet = [];
let subSum = 1;
let finalSum = 0;
let calculate = false;
let temp = [];
let answer = [];
for (let i = 0; i < clothes.length; i++) {
clothesHash[clothes[i][1]]
? (clothesHash[clothes[i][1]] = ++clothesHash[clothes[i][1]])
: (clothesHash[clothes[i][1]] = 1);
}
for (let i in clothesHash) {
closet.push([i, clothesHash[i]]);
}
let checkArr = Array.from({ length: closet.length }, () => 0);
// subset
function subset(type) {
if (type > closet.length - 1) {
// checkArr에 따라서 옷종류를 고르고 있음
for (let i = 0; i < checkArr.length; i++) {
if (checkArr[i] === 1) {
subSum *= closet[i][1];
calculate = true;
}
}
// 고른 옷에 해당되는 옷의 갯수를 곱해서 경우의 수를 구하고 누적
if (calculate) {
finalSum += subSum;
subSum = 1;
calculate = false;
} else {
subSub = 0;
}
} else {
checkArr[type] = 1;
subset(type + 1);
checkArr[type] = 0;
subset(type + 1);
}
}
subset(0);
return finalSum;
}checkArr, 그에 해당되는 옷의 종류의 갯수, finalSum, subSum, closet, clothesHash 를 출력해보면 아래와 같다.
// closet
["headgear", 4]
["eyewear", 3]
["shoes", 5]
// clothesHash
eyewear: 3
headgear: 4
shoes: 5
//checkArr, 그에 해당되는 옷의 종류의 갯수, finalSum, subSum
checkArr: (3) [1, 1, 1] (headgear, eyewear, shoes를 모두 선택하는 경우)
그에 해당되는 옷의 종류의 갯수: (3) [4, 3, 5]
finalSum: 60 / subSum: 60
(3) [1, 1, 0]
(2) [4, 3]
72 12
(3) [1, 0, 1]
(2) [4, 5]
92 20
(3) [1, 0, 0]
[4]
96 4
(3) [0, 1, 1]
(2) [3, 5]
111 15
(3) [0, 1, 0]
[3]
114 3
(3) [0, 0, 1]
[5]
119 5
// 아무것도 안입은 경우
(3) [0, 0, 0]
[]조금 복잡하긴 하지만 그래도 해내긴 해냈다!! 더군다나 내가 배운것을 활용해서 답을 구해냈다. 이건 진짜 공부이고 성장이다. 진심으로 감사하다 나에게 도움을 준 사람들에게.
그러나 훨씬 깔끔하게 만들 수 있는 방법이 역시나 있었다.
function otherSolution(clothes) {
let answer = 1;
let obj = {};
for (let i = 0; i < clothes.length; i++) {
obj[clothese[i][1]] = (obj[clothese[i][1]] || 1) + 1;
}
for (let key in obj) {
answer *= obj[key];
}
return answer - 1;
}충격적일정도로 깔끔해졌다 ㅋㅋㅋㅋㅋ 약수의 개수를 구하는 공식과 같다.
위의 내용을 잘 참고하길 바란다. 한마디로 h^4 e^3 s^5 의 곱하는 경우의 수를 구하면 되는 것이다. headgear eyeglasses shoes가 뭔지는 상관없다. 이들이 몇개 있는지 알아낸 다음 그 것들이 골고루 짝을 이루었을때의 경우의 수를 구하는 것이다.
예를 들어서 , 모자가 1개, 안경이 2개 라고 했을때
H^1 * E^2 = STH 이라고 봐도 된다. STH은 중요하지 않다.
이걸 표로 나타내보자.
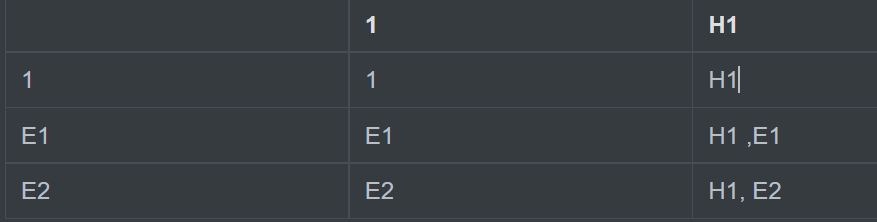
요런식으로 경우의 수가 만들어 진다.
answer -1에서 -1은 1끼리 만 짝을 지었을경우, 즉 여기서는 아무것도 입지 않았을때를 뜻한다.
약수의 개수 구하기를 떠올리다니... input과 경험치가 많으면 그러한 발상을 할 수 있는 확률이 높아지는 것 같다.
또는 모든 경우의 수를 표를 통해서 시각화 시키고 거기서 규칙을 찾아내라! 그럼 복잡하지 않고 아주 단순해 진다.
단순하게 만드는게 관건이다!
일단은 많이 풀고 정리하고 적용하자!
