키워드는 결국 #DATA라는 것!
데이터를 어떻게 정리하느냐, 어떤 데이터구조를 사용하느냐에 따라서 어플리케이션의 성능과 직결된다.
4가지 오퍼레이션 상황
1. SEARCH 검색 2. READ 읽기 3. INSERT 삽입 4. DELETE삭제
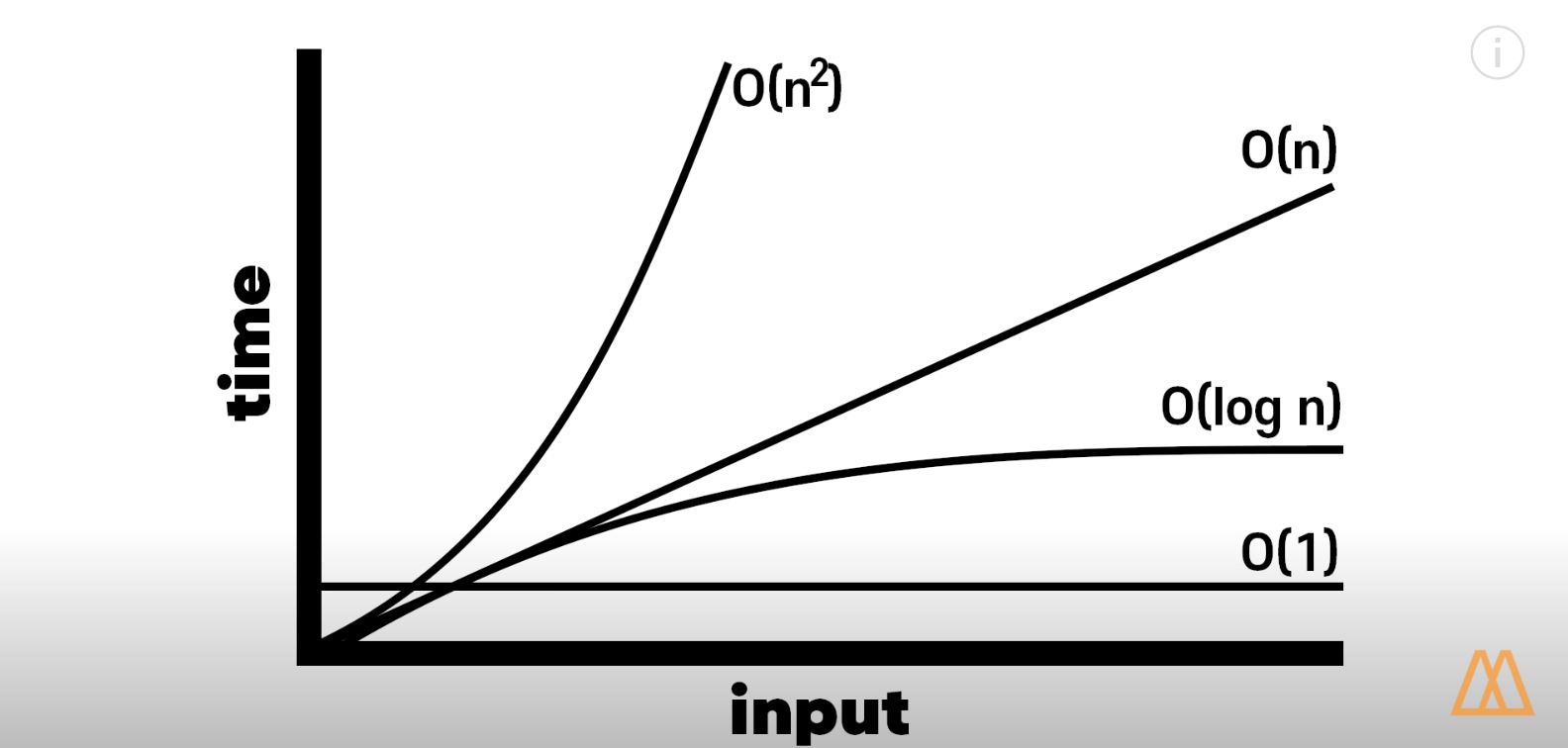
알고리즘의 시간복잡도(Big O)는 시간의 빠르고 느림을 표현하지 않고 완료까지 걸리는 절차의 수(step)로 결정된다. 컴퓨터의 하드웨어가 속도를 결정하기 때문
빅오는 인풋이 증가하면 Step이 선형적으로 증가한다는 그 원리만을 본다. 함수의 디테일에는 관심이 없다.
선형검색(linear search)
처음부터~끝까지 reading
이진검색(Binary search/로그시간)
정렬된 구조에서만 사용 가능하다. 각 프로세스 스텝을 절반으로 나눠서 진행한다. 따라서 인풋사이즈가 더블이 되어도 스텝은 1만 증가함을 알 수 있다.
- e.g) 10개의 아이템이 20개가 되어도 스텝은 3번에서 4번으로 1만 증가
2차시간(Quadratic time)
배열의 각 아이템에 반복적인 루프를 실행하는 경우를 말한다.
- e.g) 인풋이 10이라면 100번의 스텝이 필요하다. 루프 안의 루프에서 함수를 실행하기 때문이다.
SORT
버블정렬(bubble sort)
순차적으로 두 가지를 비교하고 스와핑하는 것을 반복한다.
선택정렬(selection sort)
가장 작은 수를 찾아 그 위치를 변수에 저장하고 비교할 다음의 수의 위치를 찾아 저장하고 비교한다. 정렬된 부분을 제외하고 그 다음 작은 숫자를 찾고 위치와 비교한다.
삽입정렬(Insertion sort)
기준을 인덱스[1]로 뒤고 왼쪽에 인덱스에 해당하는 수보다 큰 숫자가 있는지 비교한다. 해당 되는 수는 기준 숫자의 오른쪽으로 스와핑한다.
- 버블솔트/선택정렬/삽입정렬 방법과 걸리는 시간은 다르지만 모두 빅오의 시간은 같다. 스텝의 증가 평균을 비교하기 때문
해시테이블
key와 value로 배열에 접근한다.
키를 해시함수에 넣으면 숫자로 변경(index) 해당 인덱스로 찾는다.
+collision 해시충돌: 각기 다른 키에 대하여 해시함수가 동일한 인덱스를 준 경우 => 동일한 공간에 또다른 배열을 만든다. => 배열 안에서 선형검색을 한다.
때문에 항상 상수시간은 아니라고 할 수 있는데 충돌이 있을 수 있고, 거기에서 선형검색을 하는 시간이 있기 때문이다. 하지만 빅오는 평균을 비교하기 때문에 시간복잡도는 O(1)로 표현된다.
상수시간 > 로그시간(이진검색) > 선형검색 > 2차시간/지수시간
😅
알고리즘과 자료구조 노마드코더 내용 정리
https://www.youtube.com/watch?v=HraOg7W3VAM&list=PL7jH19IHhOLMdHvl3KBfFI70r9P0lkJwL&t=4s
