[백준] 1915번 가장 큰 정사각형 (Python)

서링·2023년 4월 12일

문제

백준 1915번: 가장 큰 정사각형
https://www.acmicpc.net/problem/1915

🔅 풀이에 들어가기 앞서

저는 문제에서 주어진 nxm의 0, 1로 된 배열을 array라는 변수명으로 선언하여서 풀었습니다.
이어지는 풀이에서는 해당 배열을 편하게 array라고 부르겠습니다.

array = [input().strip() for _ in range(n)]

풀이

이 문제는 DP문제입니다. 먼저 DP 배열을 (n+1)x(m+1) 크기로 선언해줍니다.

n행 m열이 아닌 (n+1)행 (m+1)열로 선언해준 이유는 점화식을 사용할 때, "i - 1 > 0 or j - 1 > 0" 과 같은 조건을 체크하지 않기 위해서 입니다.

점화식은 다음과 같습니다.

dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1], dp[i][j - 1]) + 1

여기서 dp[i][j]는 i행 j열의 칸이 오른쪽 아래 모서리 칸이 되는 가장 큰 정사각형의 길이가 됩니다.

예시를 통해 좀 더 자세히 살펴보겠습니다.

예시 1

? 로 표시된 dp[2][3]에는 어떤 값이 들어가야 할까요?

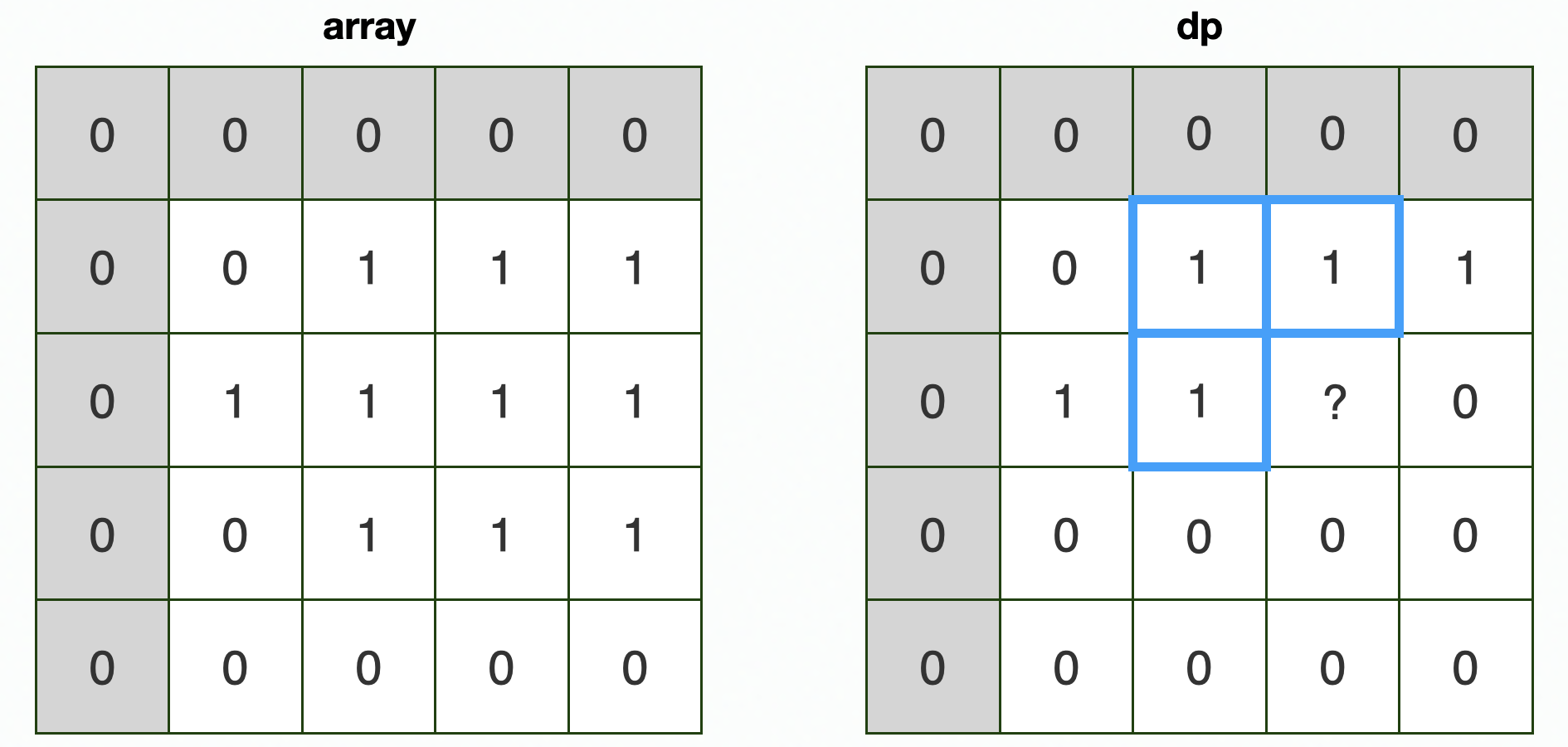
👉 위의 점화식을 사용하면, dp[2][3] = min(dp[1][3], dp[1][2], dp[2][2]) + 1 = min(1, 1, 1) + 1 = 2 이므로 dp[2][3] = 2 가 됩니다.

예시 2

dp[3][2]에는 어떤 값이 들어가야 할까요?

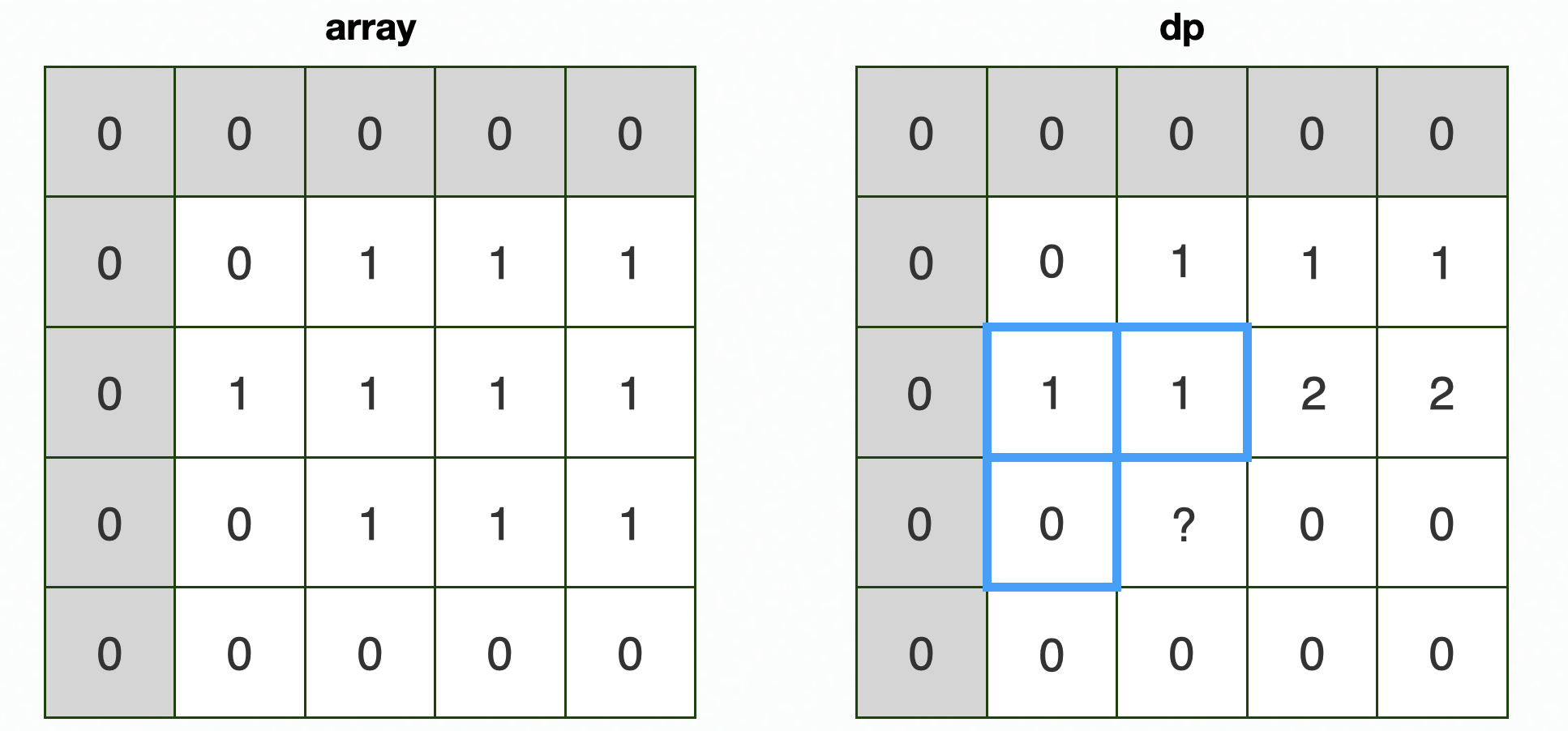
👉 dp[3][2] = min(dp[2][2], dp[2][1], dp[3][1]) + 1 = 1 이므로 dp[3][2] = 1 이 됩니다.

예시 3

dp[3][4]에는 어떤 값이 들어가야 할까요?

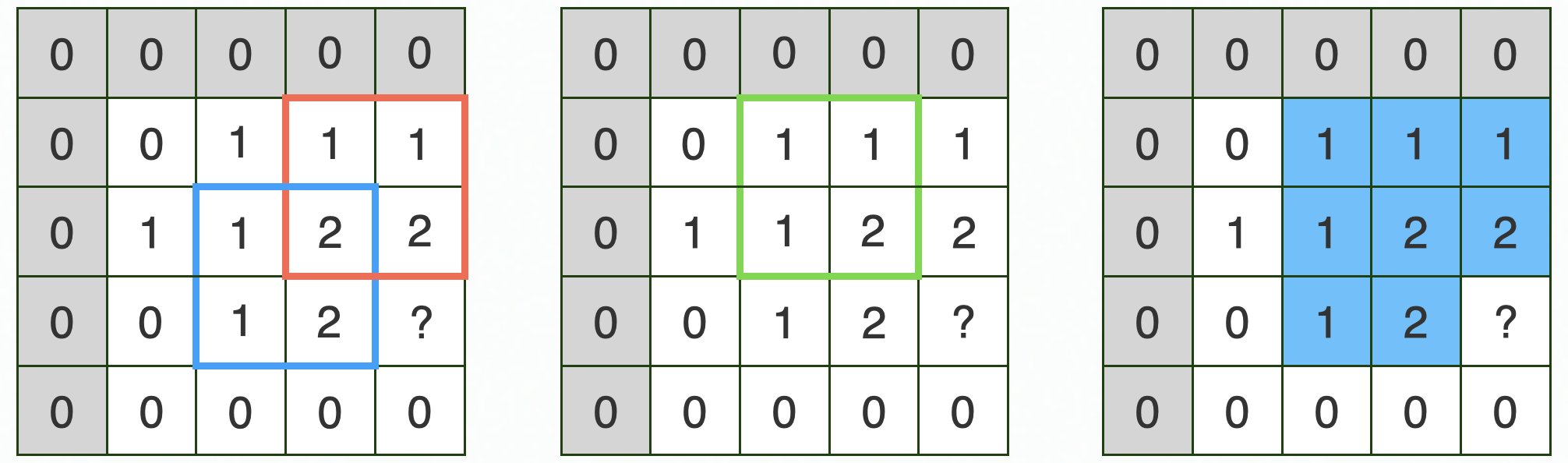
👉 dp[3][4] = min(dp[2][4], dp[2][3], dp[3][3]) + 1 = 3 이므로 dp[3][4] = 3 이 됩니다.

문제 풀 때 주의점❗️

점화식을 적용하기 위한 한 가지 조건이 있습니다.

바로 array의 값이 '1'이여야 합니다.

예제3️⃣을 보면 min(dp[2][4], dp[2][3], dp[3][3])은 2 이므로 총 길이 3짜리 정사각형을 만들 수 있었지만, dp[3][4]가 '0'이였다면 정사각형이 아니게 되겠죠?

코드

n, m = map(int, input().split())
array = [input().strip() for _ in range(n)]
dp = [[0] * (m + 1) for _ in range(n + 1)]
max_length = 0

for i in range(1, n + 1):
    for j in range(1, m + 1):
        if array[i - 1][j - 1] == '1':
            dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1], dp[i][j - 1]) + 1
max_length = max(map(max, dp))

print(max_length ** 2)