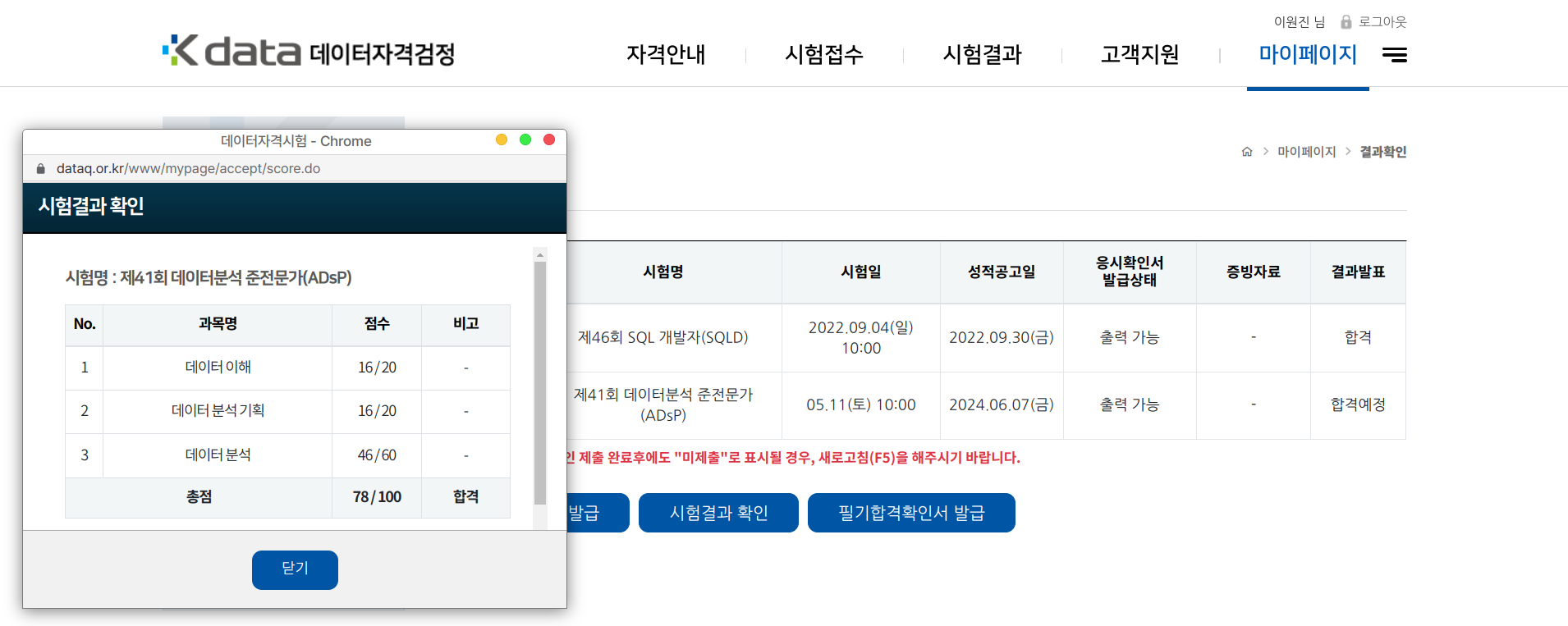
결과

합격

후기

2024년 5월 11일 41회 응시.
1, 2과목은 다들 어렵다는 평이 많았는데, 난 쉬웠다.
상식적, 논리적으로 생각하면 쉬운데, 암기로 해결하려하면 안되는 문제들이었다. 다만 애매한 표현이 많아서 헷갈렸다. 기존 기출과는 문제 유형이나 표현이 아예 달랐다.

3과목은 이전 기출에 비해 많이 어려웠다. 책이나 기출문제에서 나오지 않은 것들이 많이 나오기도 했고, 표현을 꼬아놓은 문제가 많았다. 시험이 거듭되고 작년, 올해 합격률이 높아서인지 합격률을 조절하려 한다는 느낌을 받았다.

몇 문제 차이로 아쉽게 탈락하거나 턱걸이 할 것 같다.
카페에서 복기된 문제로 보면 굉장히 잘 본 것 같지만, 공식 답안이 아니니 확신할 수가 없다.

빅분기부터 문제를 애매하게 내거나 말장난을 하는 경향이 포착되었다고 한다. ADsP에도 그런 기조가 반영된 듯

목적

• 2024-상반기 자격증 겁나빨리많이따기 프로젝트의 일부
• 데이터분석에 대한 개략적인 이해
• 노동경제학 과제를 하기 위한 빠른 배경지식 습득 필요.
• 나중에 사업계획서 쓸 때 설득력을 높이기 위해 쓸 수 있을듯.

전략

1, 2 과목은 시험 당일날 인터넷에 떠도는 요약본 보고 잘 찍는다
3과목만 대충 다 공부한다

---

R기초와 데이터 마트

R기초

R은 오픈소스 통계분석 도구. 개발환경(IDE)는 RStudio

데이터 타입

• character. "epita" or 'sejong'
• 숫자
  • 세부 타입 : numeric, double, integer, complex
  • 상수 : Inf, -Inf
• 논리 : TRUE, FALSE
• 기타
  • NaN : 숫자 아님 (에러메시지에 가까움)
  • NA : 결측치. 공간 차지.
  • NULL : 결측지. 공간 차지 안함. 존재하지 않는 값.

연산자

• 대입
  • 왼쪽을 오른쪽에 : -> ->>
  • 오른쪽을 왼쪽에 : <- <<- =
• 비교
  • == != < <= > =>
  • is.character is.numeric is.logical is.na is.null
  • 참고 : NA랑 비교하면 NA반환
• 산술
  • + - * /
  • %/%나눗셈 몫, %%나눗셈 나머지
  • 거듭제곱 : ^ **
  • 자연상수 거듭제곱 : exp()
• 논리 : ! & |

제어문, 함수

# if
if () {}
else if () {}
else {}

# for
for (i in 1:3) {}

v = c(1,2,3)
for (i in c) {}

# while
while (i<10) {i = i+1}

# function
f <- function (n) {} # def
f(42) # call

자료구조

참고. rbind, cbind를 사용할 수 있는 경우는

• vector : 결합이 언제나 되긴 하는데, 개수 다르면 적은벡터가 재사용됨. 오류발생

• matrix, array : 결합대상 방향의 원소 개수가 같아야 가능

• vector : 같은 자료형 1차원 저장

  • v = c(1, 2, 3) v = c(1:42)
  • 결합 : rbind(v1, v2), cbind(v1, v2)
  • 다른 타입 들어오면 첫 번째 원소의 타입으로 통일시켜버림
  • 주 의 : 인덱스 시작 1임. 0아니다!! 0아니다!!!!!!!!

• matrix : 2차원 벡터

  • 기본적으로 첫 열부터 위->아래 순서로 채운다.
  • byrow=T 옵션을 넣으면 첫 행부터 왼->오른 순서로 채운다.

# 만들기
m = matrix( c(1:8), nrow=4 )
m = matrix( c(1:8), ncol=4 )
m = matrix( c(1:8), ncol=2, byrow=T )

v = c(1:8) # 1차원 벡터
dim(v) = c(2,4) # 2*4 매트릭스

# 행 열 이름짓기, 접근하기
colnames(m) = c('c1', 'c2')
colnames(m) # c1 c2
rownames(m) = c('r1', 'r2', 'r3', 'r4')
rownames(m) # r1 r2 r3 r4

# 접근
print(m[4, 2])
print(m[ , 'c2'])
print(m['r1', ])

• array : 3차원 이상 벡터

# 만들기
a = array( c(1:16), dim = c(2, 2, 4) )

a = c(1:16)
dim(a) = c(2, 2, 4)

# 행 열 이름짓기
dimnames(a) = list(c('x1', 'x2'), c('y1', 'y2'), c('z1', 'z2', 'z3', 'z4'))

# 접근
print(a[1,1,2])
print(a['x1', 2, 4])

• list : 데이터 타입, 구조 상관없이 다 때려박을 수 있음

l = list()
l[[1]] = 'hi'
l[[2]] = array( c(1:32), dim = c(4, 4, 2) )

• data.frame : 2차원 관계형 데이터 구조
  • 매트릭스랑 다르다 : 각 열은 별개의 벡터. 열마다 데이터타입 달라도 됨.

vc = c('a', 'b', 'c')
vn = c(123, 456, 42)
vb = c(TRUE, FALSE, TRUE)
df = data.frame(vc, vn, vb)

# 접근
df$vc[2]
df$vb[3]

내장함수

• 기타

# 도움말
help # 또는 ?
# 문자열 더하기
paste('hi', 'hello') # hi hello
# 수열
seq(5,30,by=5) # 5 10 15 20 25 30
# 반복
rep(42, 3) # 42 42 42
# 변수 삭제
a=1
rm(a) # 이후 a 접근하면 없다고 에러남
# 변수 리스트업
ls()
# 출력
print()
# 라이브러리 설치하기, 쓰기
intall.packages('이름')
library(이름)
# 작업디렉토리 읽기, 지정하기
getwd
setwd

• 통계 : 벡터 v에 대해
  • sum(v), mean(v), median(v), var(v), sd(v), max(v), min(v)
  • 최대값과 최소값 : range(v)
  • 요약값 : summary(v)
  • install.packages('fBasics'), `library(fBasics)
    • 왜도 : skewness(v)
    • 첨도 : kurtosis(v)
• 숫자 연산 : sqrt, abs, exp, log, log10, pi, round,ceiling, floor
• 문자 연산
  • tolower('S'), toupper('S'), 문자열 길이 nchar('S')
  • 일부 추출 substr('abc', 2, 3), 분할 strsplit('a c', ' ')
  • 주어진문자 있는지 grepl('a', 'i have a')
  • 일부 문자열 대체 gsub('from', 'to', 'change from')
• 벡터 연산 :
  • 길이 length, 구분자 기준 결합 paste
  • 공분산 cov, 상관계수 cor
  • 데이터 개수 table, 벡터 순서 order
• 행렬 연산 : 전치행렬 t, 대각행렬 diag, 행렬곱 %*%
• 데이터 탐색 : head, tail, 수치벡터4분위수 quantile
  • head tail 기본값 6)
• 데이터 프레임 전처리 :
  • 조건에 해당하는 데이터만 남기기 subset(df, x=2)
  • 열 기준 결합 merge(df, df, by=c('x'))
  • 행 or 열별로 함수 적용 apply(df, 1 or 2, func)
• 정규분포
  • 기본값은 mean = 0, sd = 1
  • 함수값 dnorm(), 넓이 qnorm()
  • i개 표본추출 rnorm(i, m, sd), i보다 작을확률 pnorm(i),
• 표본추출 : 균일분포에서 runif, 주어진 데이터에서 sample
• 날짜 : Sys.Date, Sys.time, as.Date, format, asPOSIXct, unclass
• 산점도 : 산점도 plot, 추가 직선 abline
• 파일입출력 : read.csv, write.csv, saveRDS, readRDS

데이터 마트

데이터 마트 개발

• 데이터 마트 : data warehouse로부터 사용자가 원하는 데이터를 주제/부서별로 추출해서 모은 것. (작은 data warehouse.)
• 수집. 변형. 적재 = 데이터마트 개발

효율적 개발을 위해 패키지 활용.

• reshape : 특정 변수로 나눠서(녹여서) 다시 유연하게 재구성, 총계처리.
  • 특정 변수로 나누기 melt
  • 나누어진 데이터 재구성cast.
• sqldf : 표준SQL로 Dataframe 다루기
• plyr : apply함수로 데이터 분리,결합하는 기능.
  • ddply함수 중요.
  • 메소드 이름 : <입력><출력>ply()
    • e.g., laply()는 list -> array. dlply()는 dataframe->list
  • 메소드 파라미터 : (입력, 함수, 요약 or 추가, 열 이름=값, 열 이름=값, ..)
    • 두 번째 파라미터. 미리 정의된 함수 두 가지 : summarize(요약), transform(열 추가)
• data.table : 데이터프레임같은건데, 칼럼별로 인덱스 생겨서 좀 빠름.
  • 탐색, 연산, 정렬, 병합 빠름
  • dt <- as.data.table (데이터프레임)

데이터 전처리

가 포함하는 일

정제 : 결측값, 이상값 처리
분석변수 처리 : 변수 선택, 차원 축소, 파생변수 생성, 변수 변환, 불균형 데이터 처리

변수의 종류

• 요약변수 : 데이터로부터 추출한 기본적 통계자료. (e.g., 합계)
• 파생변수
  • e.g., 12월 주차별 20대 구매량
  • 특정 목적, 조건을 붙여 새로 만든 변수. 주관적일 위험. 논리적 타당성 필요.

결측값 처리와 이상값 검색

EDA : 탐색적 데이터 분석

Exploratory Data Analysis

• 왜 : 데이터 이해, 유의미한 관계를 찾기 위해
• 하는일 : 시각화, 분석하는 것
• 의의 : 데이터 특성 이해를 통해 분석 모델 구축.

str(df) 함수가 보여주는 것

• 데이터 타입, 행(observation)/열(variable) 개수
• 변수 목록과 타입

결측값

이 뭐임?

존재하지 않는 데이터. 표현되는 예시는

• NA (일반적)
• 데이터수집환경에 따라 다르게 표현될수도 : null, -1, 공백

보통 어떻게 처리함?

• 지워버림
• 하지만 결측값이 있다는 것 자체가 중요한 의미일 수도 있음. (민감도 등)

결측값 처리를 위한 패키지 있음

• Amelia : missmap 함수로 결측값 시각화.
• DMwR2

결측값 대치 방법

단순 대치법

• 결측값 있는 데이터 삭제. 대량 데이터 손실 발생 가능성.
• complete.cases(df) : 결측값 있는 column없으면 TRUE. 하나라도 있으면 FALSE.

평균 대치법

• mean or median으로 결측값 대치 --> 불완전한 자료를 완전한 자료로
• 세부 종류
  • 비조건부 평균 대치법 : 그냥 전체 평균값으로 바꿔버림
  • 조건부 평균 대치법 : 회귀분석 활용해서 구간의 적절한 평균값으로 대치.
• DMwR2.centralImputation(df)

단순 확률 대치법

• 평균대치법의 '추정량 표준 오차의 과소 추정 문제' 보완
• knnImputation(df, k = 이웃개수)
• 문제 : k 몇개 골라야될지 결정하기 어려움

다중 대치법

• 여러 대치법 돌려서 n개의 임의 완전자료 만들기.
• 단계 : 결측값 대치 - 분석 - 결합.
• Amelia(df, m, cs)

이상값

좀 튀는 값. 너무너무 크거나 너무너무 작거나.
생기는 이유 : 입력 실수. 악의적인 설문응답.
제거하는 경우 많지만 이상값 자체가 의미가 있을 수 있음.

이상값 판단 방법

• ESD (Extreme Studentized Deviation)
  • 평균으로부터 std=3만큼 떨어진 값 --> 을 이상값이라고 판단
  • 근거 : 정규분포에서 99.7%는 std=3 범위 안에 있음. (즉, 0.3%는 이상값으로 간주)
• 사분위수
  • 배경지식
    • IQR(사분범위) : Q1(25%)과 Q3(75%)의 사이 = 사분위의 정상 범위
    • Q2 = 중앙값
  • 사분범위에서 1.5분위수 벗어나는 값 = 이상값
    • 즉, P = {x | Q1 - 1.5*IQR > x 또는 Q3 + 1.5*IQR < x}

---

통계분석

통계학 개론

배경지식

• 표본조사
  • 표본집단 : 모집단을 대표할 수 있는 부분집단. 신뢰할 수 있는 '표본의 대표성' 필요.
• 통계 : 분석하려는 집단을 조사, 실험해서 얻는 자료. 요약된 형태도.
  • 기술통계 : 표본 자체의 특징 파악에 중점. 요약, 조직화, 단순화.
  • 추리(추론)통계 : 수집한 데이터로 추론(예측)하는 것. 모수의 확률적 추정. 모집단의 특성 추정. 가설 검증. 확률적 가능성 파악.
• 통계학 : 불확실한 상황에 의사결정 잘 할 수 있게 자료 수집해서 뭐 잘 하는법 연구하는 학문

표본 추출

같은 추출법이라도 복원 추출을 할지, 비복원 추출을 할지 결정해야 함.

• 단순 랜덤 추출법 : 랜덤으로 n개 추출
• 계통 추출법 : k개 건너서 n개 추출. 비복원추출방법.
• 집락(=군집=클러스터) 추출법 : 단순 랜덤 추출법으로 집락 선택.
  • 같은 집락끼리 이질적. 다른 집락끼리 동질적.
• 층화 추출법 : 집락 추출법 반대로.
  • 같은 집락끼리 동질적. 다른 집락끼리 이질적
  • 비례층화추출법 : 군집별 추출 개수 비율 = 전체 데이터 분포 비율
  • 불비례층화추출법 : 전체분포비율 신경안쓰고 원하는만큼 각 집락에서 선택

척도

• 측정 : 표본조사 할 때 목적에 맞게 관측해서 자료를 얻는 것
• 척도 : 측정한 것을 숫자로 바꾸는 규칙. 도구.
  • 질적 척도
    • 명목 척도 : 어느집단에 속함?
    • 순서(서열) 척도 : 서열관계가 있는 명목척도.
  • 양적 척도
    • 구간(등간) 척도 : 속성의 양 측정 가능. 구간 사이에 의미 있음
    • 비율 척도 : 절대적 기준(0)이 존재해서 사칙연산이 가능한 구간척도.

확률

확률 : P(A) = 사건 A 개수 / 전체 사건의 개수

• 전체 사건의 개수 = 표본공간
• 0~1사이. 가능한 모든 사건의 확률의 합 = 1

조건부 확률 : P(B|A) = P(B ^ A) / P(A)

사건의 종류

• 독립사건 : A,B가 독립 -> P(B|A) = (B)이고 P(A ^ B) = P(A)P(B)
• 배반사건 : A,B가 동시에 일어날 수 없음 -> A ^ B = 공집합

확률변수 : 무작위 실험 했을 때 특정 확률로 발생하는 각 결과를 숫자로 표현하는 변수

• 이산확률변수 : 취할 수 있는 값이 유한함. (가산)
  • 서로 배반인 사건의 합집합 확률 = 각 사건의 확률의 합
• 연속확률변수 : 취할 수 있는 값이 무한함. (특정 구간의 전체에 해당)

확률분포 : 확률변수와 그에 대응하는 확률의, 분포.

• 이산확률분포 :
  • 베르누이 분포 : 경우의 수 2가지에서 성공할 확률 p인 분포
  • 이항분포 : n번 베르누이 시행에서 k번 성공할 확률의 분포,
  • 기하분포 : 베르누이 시행 처음으로 성공할 때 까지 k번 실패할 확률의 분포
  • 다항분포 : 경우의 수가 3개 이상인 경우의 이항분포
  • 포아송 분포 : 단위 시간/공간 내에서 발생할 수 있는 사건의 발생 횟수에 대한 분포
• 연속확률분포 :
  • 균일 분포 : 확률변수의 모든 값에 확률이 똑같
  • 정규 분포 : 생각하는 그거 맞다. 정규분포를 따르는 확률변수 X
    • 표준 정규분포 : 평균=0, 표준편차=1인 정규분포. 표준정규분포를 따르는 확률변수 Z
    • 표준화 : X를 Z로 바꾸는 것. $Z = \frac{X-μ}{σ}$ ~ $N(0, 1^2)$
  • t 분포 :
    • 자유도=n인 t-분포 -> 평균0이고 좌우대칭 종모양 -> 정규분포보다 두꺼운 꼬리
    • 표준정규분포로 모평균 구하고 싶어도 모표준편차를 모르니까, 대신에 t-분포를 검정통계량으로 활용.
  • 카이제곱 분포
    • 표준정규분포를 따르는 확률변수들의 제곱의 합(X)이 따르는 분포.
    • 모평균/모분산을 모르는 여러 집단 사이의 동질성검정, 모분산검정에 사용
  • F 분포
    • 서로 독립인 두 카이제곱분포를 따르는 확률변수 2개를 각각의 자유도로 나누었을 때 서로의 비율X -> 자유도가 k1, k2인 F분포를 따름.
    • 등분산검정, 분산분석에 사용

확률함수 : 확률변수를 확률에 대응시키는 함수

• 확률 질량함수 : 이산확률분포의 확률함수
• 확률 밀도함수 : 연속확률분포의 확률함수 (그래프 아래 면적=확률)

기댓값

• 특정 사건이 시행됐을 때 확률변수X가 취할 수 있는 값의 평균.
• 기댓값 E(X) = X의 값 * X가 발생할 확률의 곱들의 합

분산 : 데이터가 중심에서 떨어진 정도. 차이의 제곱의 평균

• 확률변수의 분산 : 확률변수가 취할 수 있는 값이 모평균(중심)에서 얼마나 떨어져있냐? ( 크다 = 확률x값이 기댓값에서 멀다 )

표준편차 : 자료의 산포도. 분산의 제곱근.

첨도 : 확률분포의 뾰족한 정도. 3에 가까울수록 정규분포 모양. (3 빼서 0을 기준으로 하기도 함)

왜도 : 확률분포의 비대칭 정도.

• 왜도 = 0 : 정규분포와 유사. 평균=중앙값=최빈값
• 왜도 > 0 : 왼쪽으로 쏠림. 평균 > 중앙값 > 최빈값
• 왜도 < 0 : 오른쪽으로 쏠림. 평균 < 중앙값 < 최빈값

공분산 : 두 확률변수의 상관정도.

• 공분산 < 0 : 하나 증가할때 하나 감소
• 공분산 > 0 : 하나 증가할때 하나 감소
• 공분산 = 100 : 몰라! (두 확률변수의 확률분포가 어느정도 선형성인지 모른다)

상관계수 : 공분산 / (X표준편차 * Y표준편차). -1~1사이 값을 가지고 공분산 문제를 해결함.

• 상관계수 = 0 : 상관관계 없다
• 상관계수 < 0 : 작을수록 음의 상관관계 크다
• 상관계수 > 0 : 클수록 양의 상관관계 크다.

추정

모수 추정

모수를 구하고 싶은 사람들의 험난한 여정

• 모집단의 특성(평균, 분산같은거) 구하고 싶은데 전수조사가 말이 안된다(돈도 없고 시간도 없다). 그래서 표본집단 뽑아서 표본조사 하고, 표본평균과 표본분산을 구하고, 그걸로 모집단의 평균과 분산을 추정한다. 추정한 그걸 모평균, 모분산이라고 부른다. 결국, 통계를 하는 입장에서는 모수를 구하고 싶어서 온갖 방법을 들이댄다.

그래서, 모수의 추정 방법

• 당신의 모집단 조사, 표본조사로 대체되었다.

점추정

모수(특히 모평균)을 추정할 때, 모평균을 어떤 특정 '값' 이라고 예측하는 것.
모평균을 추정하기 위해 '불편추정량' 사용

• 불편추정량 : 모수 추정값과 실제 값의 차이의 기댓값 = 0인, 편향이 없는 이상적인 값.
  • e.g., 표본평균 (=표본집단의 평균)
  • 불편추정량 중, 최소의 분산을 가진 추정량이 가장 좋은 추정량

구간추정

모수가 특정 구간안에 존재할 것이라 예측하는 것 (특정한 하나의 값이 아니고)
신뢰도(신뢰수준)이 구간추정에서 나오는 말이다. 95%, 99%를 많이 사용.

• 95% : z_0.025 = 1.96
• 99% : z_0.005 = 2.09

가설검정

통계적 가설검정 : 모집단의 특성에 대해 가설을 세우고, 표본에서 얻은 정보로 가설이 맞냐 안맞냐를 판정하는 과정

가설

• 귀무가설 $H_0$ (null hypothesis) : 연구를 통해 기각하고자 하는 가설. 기각을 통해서 주장 관철 가능.
• 대립가설 $H_1$ (alternative h) : 연구를 통해 증명하려고 하는 가설. 귀무가설이 기각되면 채택.

즉, 귀무가설을 기각하면 대립가설을 채택한다.
대립가설을 기각하면 귀무가설을 채택(해야 ㅠ)한다.

오류

• 제1종 오류 : 귀무가설이 사실인데 귀무가설이 틀렸다고 하는 것 (맞는데 아니라고)
• 제2종 오류 : 귀무가설이 사실이 아닌데 귀무가설이 옳다고 하는 것 (아닌데 맞다고)

둘은 서로 반비례 관계.

그 외

• 검정통계량 :
  • 귀무가설이 맞냐 아니냐를 판단할 수 있는 값.
  • 귀무가설 채택여부 결정을 위한 표본조사를 했을 때, 어떤 수식을 통해서 얻은 값.
• 기각역 : 귀무가설을 기각할 정도의 검정통계량 영역.
  • 즉, 검정통계량이 기각역 안에 있으면 -> 귀무가설 기각
  • 임곗값 = 기각격의 경곗값
• 유의수준($\alpha$) : 제1종오류를 허용할 최대 한계(확률). 유연하게 조절하는데 보통 1%, 5%를 씀.
• 유의확률(p-value) : 귀무가설을 지지하는 정도를 나타낸 확률값.
  • p-value < $\alpha$ : 귀무가설 기각 (아 이정도 맞을 확률이면 오키. 봐드립니다. 기각해도됨 ㄱㄱ)
  • p-value > $\alpha$ : 귀무가설 채택 (스읍... 맞을 확률 너무 커서.. 이건 기각하긴 좀... 안돼...)

모수 검정 vs 비모수 검정

모수 검정

모수적 특징(표본이 정규성을 갖는다)을 이용한 통계 방법. 지금까지 주로 살펴본 그거.

• 반대로 말하면, 정규성 없으면 모수 검정을 할 수가 없다.
• --> 그럼 어떡함? 어떡하긴 비모수 검정해야지.

등간/비율 척도. 평균. 피어슨 상관계수.

비모수 검정

모수적 특징을 이용하지 않는 검정 방식.

• 명목/서열 척도. 중앙값. 스피어만 순위상관계수.

언제씀? : 정규분포가 아닌 경우. 가정 할 수 없는 경우. (e.g., 군집당 10명 미만 소규모 실험)

구체적인 '언제'의 예시는?

• 서수데이터. 서열척도 (숫자이긴 한데, 갯수도 못세고 평균도 못내는) --> 순위 합 이용
• 이상치 때문에 평균보다 중앙값이 더 가치있는 경우
• 표본의 크기가 작은 경우

검정방법의 종류는?

• 연속성, 부호 순위, 부호, 프리드만, 순위 합, 크루스칼-월리스 검정
• 스피어만 서열상관 분석

검정

중심극한정리 : 모집단 분포에 관계없이, 표본 개수가 커질수록 표본평균 분포는 정규분포에 가까워진다. (물론 똑같지는 않다. 표본 아무리 뽑아봤자 그건 모집단이 아니다)

t-검정

t.test( 표본, 표본 또는 비교대상, 대립가설) 을 돌린다.
t는 t-value (검정통계량). df는 자유도(표본수-1).
그리고 p-value가 가장 중요. 유의수준보다 낮으면 대립가설이 맞고, 높으면 대립가설이 틀렸다.

단일(일) 표본 t검정

한 모집단의 평균값을 특정값과 비교하는 경우 사용

• 단일 표본 단측 t검정 : 방향이 있는 경우 (작다, 크다)
• 단일 표본 양측 t검정 : 방향이 없는 경우 (이다, 아니다)

독립(이) 표본 t검정

독립적인 두 집단. 둘의 모수(모평균) 값이 같은지 확인.
주의 : 두 모집단은 등분산성 만족해야 함. 등분산검정(=F검정) 사전수행 필요.

• 독립 표본 단측 t검정 : 대소가 있는 경우 (A가 B보다 크다, 작다)
• 독립 표본 양측 t검정 : 대소가 없는 경우 (A는 B다, 아니다)

대응 표본 t검정

같은 대상의 두 가지 관측치에 차이가 있는지 확인 e.g.,실험 전후

t.test( before, after, 대립가설 함수, paired = TRUE )
--> 유의수준>p-value이면 before가 after보다 '대립가설 함수'하다.

e.g.,
t.test( 약 복용 전, 약 복용 후, 건강상태 나빠, paired = TRUE)
돌려본 결과가 p-value>유의수준 이면
= 약 먹기 전이 먹은 후보다 건강상태가 좋다! (귀무가설 채택)

분산분석 (ANOVA)

3개 이상 모집단. 여러 집단 사이 평균 비교. 분산 사용 (얼마나 차이남)

• 귀무가설 : 모든 집단 평균 같다
• 변수
  • 독립변수 : 범주형 데이터
  • 종속변수 : 연속형
• F-value 사용 (집단간 분산 / 집단내 분산)

유의점

• 분산분석 수행시 집단에 대한 가정
  • 정규성 : 정규분포여야해!
  • 등분산성 : 분산 똑같아야돼!
  • 독립성 : 집단끼리 서로 관련없어야돼! (영향X)
• 단점 : 귀무가설 기각하면 어느 집단의 평균이 얼마나 다른지 알 수 없음.
  • 사후검정 필요 (Scheffe, Tukey, Dunca, Fisher's LSD, Dunnett, Bonferroni)

일원분산분석

각 집단별로 : 독립변수 1개. 종속변수 1개.

https://aliencoder.tistory.com/40
SST = SSR + SSE

• SST : 전체의 변동성.
• SSE : 설명불가능한 변동성. 잔차가 표본평균에서 벗어난 편차 (의 제곱)
• SSR : 설명 가능한 변동성. 예측값과 관측값평균의 차이의 제곱.

aov( dataframe, column ~ column )
Pr>F이 p-value

이원분산분석

각 집단별로 : 독립변수 2개 이상. 종속변수 1개

• 사전 수행 : 교호작용 있냐 없냐 판단
  • 있으면 -> 반복실험
  • 없으면 -> 반복 안함

다변량분산분석(Manova, 다원분산분석)

독립변수 2개 이상. 종속변수 2개 이상.

교차분석

범주형 자료(명목, 서열)간 관계 확인. -> 적합도, 독립성, 동질성 검정에 사용.
카이제곱 검정통계량 사용

교차분석표 : 두 범주형 변수 교차. 데이터 빈도 표 형태로 시각화.

적합도 검정

실험 관측값 = 예상값 인가? 를 확인
관측도수 = 기대도수 인가? 를 확인 (같은말)

일치하면 -> 실제분포 = 예측분포

가설

• 귀무가설 : 분포 같다
• 대립가설 : 분포 다르다.

적합도 판정 방법

• 유의수준 0.05
• 기각값 : $X_{\alpha,df}$ (알파는 유의수준, df는 자유도=범주수-1)

독립성 검정

모집단이 두 개 변수에 의해 범주화 됐을 때.
두 변수가 독립적이냐 아니냐? 확인

독립적 -> 변수사이 유의관계 없다.
안독립적 -> 변수사이 유의관계 있다.

유의관계는 상관관계를 의미하지 않는다. 관계의 강도를 의미하지도 않는다.
그냥 독립성 검정 결과는 독립적인가 아닌가, 즉 유의관계가 있냐 없냐 그뿐이다.

동질성 검정

관측값들이 정해진 범주 내에서 서로 비슷하게 나타나는가?
표본값의 속성 분포 = 모집단의 속성 분포 인가?

동질성 검정통계량 계산 -> 교차표 활용.
계산/검증법 -> 독립성 검정과 동일.

상관분석

두 변수가 선형적 관계가 있는가? -> 상관계수 활용
상관계수 : -1 ~ +1 사이 값. 양쪽 끝값에 가까울수록 음의/양의 상관관계 크다.

• 상관관계의 유무로 인과관계의 유무를 알 수는 없다. 그건 회귀분석으로 알 수 있다.

산점도 행렬 : 산점도, 상관계수를 한 장에 시각화한 것.
상관분석의 귀무가설 : 상관계수 = 0

cor( 변수1, 변수2, method )

피어슨 상관분석

선형적 상관관계. 모수적 방법. 두 변수 모두 정규분포 따름.

스피어만 상관분석

비선형적 상관관계. 비모수적 방법. 두 변수는 서열척도.
관측값 순위에 대해 상관계수 사용.

회귀 분석

독립변수 x : 원인변수, 설명변수
종속변수 y : 결과변수, 반응변수

1개이상 독립변수가 종속변수에 얼마나 영향을 미치는지 추정. 얼마나 인과관계가 있냐.
산점도에 추세선 나타남 -> 경향성 띤다 -> 변수간 인과관계 있다.
설명력이 높은 회귀함수가 나왔다 -> 변수간 인과관계가 크다 -> 예측력 높다.

변수는 연속형 변수 사용. 만약 범주형이면 파생변수로 변환.
종속변수가 범주형이면 로지스틱 회귀분석 사용.

종류

• 단순회귀 : 1개 독립변수. 독립-종속 변수 직선 관계
• 다중회귀 : k개 독립변수. 독립-종속 변수 선형 관계. (1차식)
• 다항회귀 : k개 독립변수. 독립-종속 변수 2차함수 이상 관계
• 비선형회귀 : 회귀식과 미지모수가 선형관계가 아님 (지수, 로그, 삼각함수)

가정

• 선형성
• 독립성 : 예외 다항회귀(2차)
• 등분산성
• 정규성

귀무가설

회귀계수가 0이다. (통계적으로 무의미하다)

검정

분산분석표 -> 모형 적합성 검정. anova( lm(y~x) )
F검정 값(F통계량) 크다 -> 회귀계수 크다 -> 인과관계 있다 (p값 작다)
t검정 값(t통계량) 크다 -> 회귀계수 크다 -> 인과관계 있다 (p값 작다)

• t통계량 = 회귀계수/표준오차 = 변수의 Estimate / 변수의 Std.Error
  QQ-Plot 45도에 가까운 직선일수록 -> 정규분포를 따른다.
  결정계수 $R^2$ 1에 가깝다 -> 데이터가 회귀선에 밀접 분포 -> 모형의 설명력 크다
• $R^2 = \frac{Q-Q_e}{Q} = \frac{SSR}{SST} = \frac{1-SSE}{SST} = \frac{1-SSE}{SSE+SSR}$
  • SSR = X의 Sum Sq
  • SSE = Residuals의 Sum Sq
• 수정된 결정계수 $R^2 = 1 - \frac{(n-1)(1-R^2)}{n-p-1}$ (n:표본크기, p:독립변수 개수)
• 보통 수정된 결정계수는 결정계수보다 작다.

단순선형회귀분석

독립변수1개. 종속변수 1개. 둘의 인과관계. 선형.
최소제곱법으로 직선의 방정식 획득.

다중선형회귀분석

독립변수 2개 이상. 종속변수 1개. 선형.
회귀계수 개수 = 독립변수 개수.

다중공선성

독립변수간 상관관계 있는 것.
-> 독립성 위배 -> 해결해야된다.

진단 : 결정계수 값 크지만(설명력 높지만), 독립변수 p값이 큰(개별인자가 유의하지 않은)경우.

• 분산팽창요인 (VIF) = 1 / (1-$R^2$) > 10이면 보통 다중공선성 있다.

해결 :

• 문제가 되는 변수 제거
• 주성분 개수 선택 : 스크리 산점도(Scree plot)
• 차원축소 : 주성분분석(PCA), 선형판별분석(LDA), t분포 확률적임베딩(t-SNE), 특잇값 분해(SVD)

최적회귀방정식

종속변수를 유의미하게 만드는 독립변수 선택.
(즉, 결과적으로는 종속변수가 가장 잘나오는 모델=회귀식 만들기)

변수 선택 방법

• 결정계수 활용
• 부분집합법(embedded) : 가능한 모델 싹다 돌려서 좋은 모델 고르기.
  • 장점 : 변수 적으면 좋은모델 효과적으로 도출 / 단점 : 변수 많아지면 모델 많이돌려야됨.
  • 라쏘, 릿지, 엘라스틱넷
• 단계적 변수선택법(Wrapper) : 일정단계 통해서 변수 추가제거
  • 장점 : 높은 정확도 / 단점 : 고비용. 과적합.
  • 전직선택법, 후진제거법, 단계선택법
• Filter : 변수집합 F에서 적합도평가지표로 변수 선택 -> 부분집합 구성.
  • 장점 : 과적합 회피, 저비용 / 단점 : 래퍼 대비 저성능

변수 선택 성능지표

참고 : 회귀모형은 변수 많아질수록 편향 적고 분산 커짐. 패널티 적을수록 좋은 모형.

• 패널티(벌점화) 방식 :
  • AIC (아카이케정보기준): MSE에 변수 개수만큼 패널티. 표본 커지면 부정확. (회귀분석 모델 선택에 많이사용)
  • BIC (베이즈정보기준) : AIC보완. 변수 개수 적으면 AIC보다 BIC 먼저 고려. (변수 많을수록 패널이 더 많이때린다)
  • Mallow's Cp : 모든 변수가 다 포함된 경우 Cp = p-value. Cp>p-valud이면 나쁜 모델. 좋은모델이면 일단 Cp<p-value.

단계별 변수 선택법 : 자세히 보기

전진 선택법 (forward) : step( lm(), scope, direction='forward')

• 영향 큰 (p-value작은) 변수 하나씩 추가.
• 추가 끝내는 시점 : '상관계수 절대값이 가장 큰 변수'에 대해 부분F검정한 결과 유의하지 않은 경우까지 추가.
• 안정성 부족 (변수값 조금만 변해도 결과에 큰 영향)

후진 제거법 (backward) : step( lm(), scope, direction='backward')

• 일단 독립변수 전부다 추가한 다음, 영향 작은(p-value큰) 변수 하나씩 제거
• = '상관계수 절대값이 가장 작은' 변수에 대해 부분F검정한 결과 유의하지 않은 변수부터 제거
• 장점 : 모든 변수 정보 이용 / 단점 : 변수 너무 많으면 적용 어려움

단계별 바법 (stepwise) : step( lm(), scope, direction='both')

• 전진선택법 후진제거법 보완.
• 전진선택법으로 추가. 하면서. 추가 패널티와 제거 패널티가 가장 작도록 동작.

고급회귀분석

정규화선형회귀

과적합(과대적합, 오버피팅) : 모델이 학습데이터를 과하게 학습. 일반화 성능 저하.
과소적합 : 모델이 너무 단순. 학습데이터도 예측못함. 일반화 성능도 당연히 낮음.

회귀분석에서 과적합 발생 -> 계수 크기 과하게 증가
하는 상황을 방지 하는 방법 = 계수 크기 제한

계수 크기 제한 하는 회귀 = 정규화 선형회귀.

e.g.,
Ridge(L1규제) : 가중치 절대값 합 최소화. 불필요 가중치 파라미터 0.(분석제외)
Lasso(L2규제) : 가중치 제곱합 최소화. 이상치 가중치 파라미터 0에 가깝게.
Elastic net 회귀모형 : 릿지 라쏘 결합. 가중치 절대값의 합, 제곱합 동시에 제약조건.

일반화선형회귀

종속변수의 정규성을 만족하지 않는 경우
E.G., 종속변수가 범주형 자료이거나 정규성 만족하지 못하는 경우

인데도 꾸역꾸역 회귀분석을 반드시 해야겠다고 하면
-> 종속변수를 함수f(x)로 정의 -> f(x)와 독립변수를 선형결합 -> 회귀분석 수행
이거 하는게 일반화 선형회귀.

구성요소 : 확률요소, 선형예측자, 연결함수
종류 : 로지스틱회귀(Y=범주변수 자료), 포아송 회귀(Y=도수자료->최대가능도추정MLE)

더빈 왓슨(Durbin-watson) 검정

오차항의 상관관계 - 보통 시계열에서 발생
자기상관성 : 하나의 잔차항의 크기, 이웃 잔차항의 크기 -> 일정한 관련 있는 것.

회귀분석에서 자기상관성 없어야 함. (오차항 공분산=0이어야 함)
자기상관성 유무의 검정 = 더빈왓슨 검정

더빈왓슨 통계량 값 2에 가깝다 -> 오차항 자기상관 없다. (좋아요)
0에 가깝다 -> 양의 상관관계
4에 가깝다 -> 음의 상관관계

회귀분석 평가지표

MSE : 제곱. 이상치 불리.
RMSE : 제곱. 이상치 불리.
MAE : 절댓값 .이상치 유리.
MAPE : 절댓값. 이상치 유리.

다변량 분석

다차원 척도법 (MDS)

객체간 근접성 시각화하는 통계기법. 군집분석 유사.
데이터 축소 목적. 데이터 정보속성(유사성) 파악을 위한 수단으로도 사용.

거리 = 유클리디안 거리행렬.

stress 척도. 개체의 실제거리, 추정거리 적합도 측정.
0~1사이. 낮을수록 적합도 높음.
0.05이내 적합도 좋다. 0.15이상 나쁘다.

거리측정 dist(df)

종류

• 계량적 MDS : 구간척도/비율척도 - 유클리디안 거리행렬, cmdscale
• 비계량적 MDS : 서열척도, 거리속성값으로 변환, isoMDS

주성분분석(PCA)

상관성 높은 변수의 선형결합으로 새로운 변수=주성분을 만듦
기존 변수를 요약, 축소.

목적 : 변수축소-> 모형 설명력 향상. 다중공선성문제 해결. 군집분성 성능 향상.

변수를 요약하는 것이니 손실 발생. 손실이 적은 축(분산이 가장 큰 축)으로 통일.

res = prcomp( df, center = T, scale. = T)
screeplot( res, type='lines' )
biplot(res)

평균 고유값 방법

고유값이 평균보다 작은 주성분 제거.
고유값(고유벡터의 크기) 크다 -> 높은 설명력.

시계열 예측

미래예측 forcast( model )

개요

일정시간 간격 기록자료의 특성 파악하는 분석방법.

대부분의 시계열자료 자기상관성 있음 -> 공분산 != 0
공분산 정규화 -> 상관계수

정상성 조건

• 모든 시점에 대해 평균 일정 : 비정상 -> 차분 diff
• 모든시점에 대해 분산 일정 : 비정상 -> 변환 (지수, 로그)
• 공분산은 시차에만 의존. (시점 의존 안함)

종류

• 정상성 시계열 자료
• 비정상성 시계열 자료 : 대부분이다. 근데 이거 분석 못한다. 그래서 정상으로 만들어야됨.

자기상관계수 (ACF Autocorrelation Function)

시간의흐름에 따른 자기상관관계. "시점"아님! "시간의 흐름" = 시차에 의존.
시계열자료가 시간의 흐름에 따라 일정한 패턴 가짐 -> 변수가 자기상관성 있다.

자기상관함수 활용 - 시계열자료가 시간에 의존하지 않고 무작위성을 띠는가?
-> 안띤다면 미래 예측 가능.

시차 x축, 상과계수 y축.
시차=0이면 1 (자신과의 상관계수)

부분자기상관계수(PACF Partial ACF)

두 시계열 확률변수간 상관관계만. (다른시점 확률변수 영향력 통제)
영상주는 요소 모두 배제. 순수한 두 확률변수사이의 관계 고려.

분석기법

이동평균법 : 일정기간별로 자료 묶어 평균 구하기

• 문제 : 옛날자료와 최신자료 가중치가 같음.

지수평활법 : 최근데이터에 큰 가중치. 오래된 데이터 작은 가중치.
자료 많고 안정패턴 -> 높은 예측 품질.
불규칙변동 영향 제거 가능. 중장기예측.

모형

자기회귀 모형 (AR) : 이전시점 자료값들에 의한 선형결함

이동평균 모형 (MA) : 이전시점 백색잡음들의 선형결합. (항상 정상성 만족)

자기회귀누적이동평균 모형 (ARIMA) : 비정상시계열 자료 핸들링 가능.

• ARIMA(p, d, q) : 쪼개면 AR-p, I-d, MA-q
• p=0 -> IMA
• d=0 -> ARMA
• q=0 -> ARI

분해시계열 : 추세, 계절, 순환, 불규칙

---

정형 데이터 마이닝

데이터 마이닝 개요

데이터 속의 규칙, 패턴 발견 -> 예측, 의사결정 활용.
머신러닝 구현의 바탕

통계분석 VS 데이터마이닝

• 통게분석 : 수집-정제-추정-검정 (표본이 있어야 한다. 가설이 있고 검정을 한다.)
• 데이터마이닝 : 상향식접근법. 목적정의-데이터준비-데이터가공-기법적용-검증.

방법
: 이름이 좀 괴상하게 생겼으면 비지도 학습이다 (DBSCAN, PCA, LDA 같이)
이름이 좀 정상적으로 생겼으면 지도학습일 확률 높다 (의사결정나무, 앙상블, 나이브베이즈, SVM)

• 지도학습
  • 회귀, 분류.
• 비지도학습 : 독립변수에 대한 종속변수 없다.
  • 군집, 연관, 차원축소.

분석 목적

• 분류분석 : 이질적 데이터들 비슷한것 그룹으로 묶기. 병합적, 분할적, k-mean 군집.
• 군집분석 : 장바구니분석. 데이터의 연관성 파악.
• 연관분석 : 카탈로그 배열, 교차판매, 판촉행사 --> 결과 : 연관규칙

데이터 분할

걍 데이터셋 분할하는거다.
훈련용 50퍼, 검정용 30퍼, 평가용 20퍼.
훈련용 60퍼, 검정용 20퍼, 평가용 20퍼.

훈련용 - 모델구축용
검정용 - 구축모델 적합성 검증. 과대과소 추정 방지.
평가용 - 최종구축모델 성능 평가.

파라미터(매개변수) : 그냥 있는거. 사람이 안찾아도 (회귀계수, 인공신경망 가중치)
하이퍼파라미터(초매개변수) : 모델구축 외적 요소. 사람이 찾아줘야됨 (인공신경망 은닉층 수. 은닉노드 수. knn k값.)

데이터 분할을 통한 검증 방법

홀드아웃

• 학습데이터80 테스트데이터20 / 학습데이터70 테스트데이터30
• 검증용데이터 없음. 하이퍼파리미터 튜닝단계 생략

K-겹 교차검증(K-Fold corss validation)

• 전체 데이터셋 k개로 나눔. k-1개 훈련데이터. 1개 테스트데이터.
• k개모델 구축. 종합. 최종모형 구축.
• 모델 정확도 향상. 데이터 많으면 과대과소적합 방지. 시간 많이듦.

LOOCV (Leave one out corss validation)

• N-1개 훈련용데이터. 1개 평가용 데이터.
• K겹교차검증이랑 비슷. 다만 전체 데이터 크기N으로 나눔. (K대신 N) -> K겹교차검증은 전체데이터 크기가 N이고, K개로 나눴다고 본다.

붓스트랩 : 복원추출! 중복추출허용!

• 원본데이터 크기만큼 복원추출 수행. 추정 신뢰성 평가에 사용.
• 중복추출 허용 (랜덤반복추출).
• 해결가능한 문제 : 데이터셋 고르지 않은 분포. 오버/언더샘플링 문제 해결. 과적합 발생 가능성 낮춤.
• 붓스트랩 확률
  • 하나의 데이터 뽑을 때
    • 특정 데이터 뽑힐 확률 = 1/n
    • 안뽑힐 확률 = 1 - (1/n)
  • 단 한 번도 선정되지 않을 확률 = (1-(1/n))^n
    • 무한하게 뽑으면 1/e = 36.8%가 된다.

계층별 k-겹 교차검증 (Stratified k-fold cross validation)

• 불균형데이터분류문제에 주로 하용. k-폴드 교차검증과 동일한 작동방식.
• 각 폴드가 가지는 레이블 분포 유사하게 폴드 추출. 교차검증.

오버/언더 샘플링

• 데이터 많아도 목표변수의 수 불균형 -> 잘못된 데이터 분할 -> 모델구축 학습 망함
• 좋은 데이터 목표변수 = 균형을 이룬 목표변수 -> 안정적 데이터 분할 -> 다양한 범주 학습 가능

균형맞게 데이터셋 축소 = 언더샘플링
균형맞게 데이터셋 확장 = 오버샘플링

분류분석(Classification)

로지스틱 회귀분석

회괴분석을 분류에 이용.
독립변수 선형결합 -> 사건발생가능성 예측.
독립변수 연속형. 종속변수가 범주형변수-확률값. 0~1.
0~1 확률 반환.

알고리즘

오즈 Odds = 성공횟수 / 실패횟수.

• 오즈값 = 성공확률/실패확률
• 독립변수 1증가 -> 오즈값(성공확률) e^베타 증가.
• 한계 : 음수 없다. 확률값-오즈 그래프 비대칭성.

로짓변환 Logit = log(오즈) = 오즈에 로그값 취한 것

• 오즈범위 무한대로 확장. 그래프는 성공확률 0.5기준 대칭형태.

시그모이드 sigmoid

• 로지스틱회귀, 인공신경망에서 활성화함수로 활용.
• 로짓함수의 역함수.

의사결정나무

rpart

자료학습 -> 특정분리규칙 찾음 -> 몇개 소집다으로 분류.
상위노드->하위노드 순서로 분류 : 나무기자와 유사.
의사결정 진행방식 한 눈 에 알 아볼 수 있다

올바른 분류 : 상->하 갈수록 집단내 동질성, 집단간 이질성 커져야.

깊이 = 뿌리마디 제외 . 중간마디 수.
노드를 마디라고 함. 엣지는 가지.

구성요소

• 회귀트리 : 종속변수 연속형
• 분류트리 : 종속변수 이산형.

활용 : 세분화. 분류. 예측. 차원축소/변수선택, 교호작용

특징 :

• 장 : 직관적. 해석용이. 정규화/단위변환 필요없. 전처리 쉬움. 이산/연속변수 모두 적용가능. 가정 불필요. 이상값 둔감.
• 단 : 독립변수 중요도 판단 어려움. 분류경계근근처 자료 오차 큼. 과적합 가능성 높음.

분석과정

성장

• 분리기준
  • 이산형 종속변수 : 분류트리 - 카이제곱검정 지니지수 엔트로피지수
  • 연속형 종속변수 : 회귀트리 - F통계량, 분산감소량
• 최적의 분할 : 불순도 감소량 최대화 (섞여있는거 떼내기)
• 정지규칙 : 일정깊이 도달. 불순도 감소량 일정미만. 마디 내 자료수 일정 수 이하. 모든 자료가 하나의 그룹에 속하는 경우.

가지치기

• 일부 가지 제거 -> 적당한 크기 트리 -> 과적합 제거.

타당성평가

• 검증용 데이터로 모델 예측정확도 평가. 이익도표 -> 의사결정나무 평가.

해석및예측

• 써먹기. (예측에 적용하고 해석)

앙상블분석

여러개 모형 생성, 조합 -> 예측력 높은 모형 만들기
예시 : 배깅, 부스팅, 랜덤포레스트

각각의 모델 = 분류기. 의사결정나무 많이 사용.
여러 분류기 결과를 다수결로 최종결과값 선정 = 보팅

최종결과 예측 방법

• 결과가 수치형데이터 : 값들의 평균
• 결과가 범주형데이터 : 다수결 방식.

결과보기
table(condition, pred) : condition 실제, pred 예측
pred$confusion : observ 실제, predicted Class 예측

배깅

bagging(train data, y ~ ,)

Bootstrap aggregating 여러개의 붓스트랩 집계.

붓스트랩 = 원본데이터와 같은 크기의 표본을 랜덤복원추출한 샘플데이터
훈련용데이터.

모집단 특성 잘 반영되는. 분산작고 좋은 예측력.
각 분류기(모델) 독립적.

트리 모든바디 불순도 최소화. - 최적의 분할.

OOB

• OOB(Out of bagging) : 붓스트랩 생성에 사용되지 않은 데이터.
• OOB Score : 붓스트랩으로 구성된 트리를 oob데이터로 평가. (어쩌다 보니 생긴 평가용 데이터 oob.)

부스팅

boosting(train data, Y~., boos=T, mfinal)
배깅과 유사. 차이 : 분류기가 독립적이지 않음.

다음모델 구축할 때, 이전 분류기가 잘못 분류한 것에 더 큰 가중치 -> 붓스트랩 구성
즉, 약한모델 결합 -> 점차 강한 분류기 구축
훈련오차 빠르게 줄임. 예측성능 배깅보다 좋ㅇㅁ.

종류 : AdaBOosting, GradientBoost, XGBoost, Light GBM

랜덤포레스트

randomForest (y~., train data, ntree)

서로 상관성 없는 트리로 이루어진 숲
배깅과 유사. 차이점 : 더 많은 무작위성

더 무작위하게 만든 여러개의 트리구성.
여러개의 약한 트리 선형결합 -> 최종결과.

각 마디에서 또 표본추출. 추출된 표본으로 최적의 분할 실시.
(배깅이 모든마디 불순도를 줄이는 방향으로 분할했던 것과 차이)

의사결정나무 대비 분산 감소 (개선)
높은 비상관성. 일반화성능 향상. 이상값 여전히 둔감.

즉, 복원추출 -> 붓스트랩 -> 변수 비복원추출 -> 표본 -> 분류기 -> 보팅 -> 값.

인공신경망분석

neuralnet(train data, y~. , hidden = vector변수, stepmax=1e7)

여러개의 퍼셉트론으로 구성. 각 퍼셉트론은 가중치 보유.

원리 : 값 입력 -> 개별신호 따라 가중 -> 가중된값에 편향 더함 -> 활성함수 -> 출력값.
신공신경망 등장 영향 : 머신러닝을 넘어 딥러닝 등장. CNN, RNN.
장점 : 잡음 둔감. 비선형문제 분석 가능. 패턴인식/분류/예측 잘함. 스스로 가중치학습-많은데이터 떄려넣기좋음
단저 : 모형 복잡하면 학습 오래걸림. 초기 가중치 잘못되면 지역해로 수렴. 추정 가중치 신뢰도 낮음. 결과해석 어려움. 은닉층/은닉노드 수 결정 어려움.

종류 : RNN(순환), CNN(합성곱), LSTM(장단기메모리), YOLO(이미지), GAN(생산적적대)

알고리즘

활성함수 : 노드 입력값을 출력하기 전 거치는 비선형 함수.
어떤 활성함수 쓰냐 -> 출력값이 달라짐. 적절한 함수 고르는거 중요.

퍼셉트론과 신경망의 차이는 활성함수의 차이.
퍼셉트론은 선형, 신경망은 비선형 함수 사용.

• Step. 0 or 1
• Sigmoid : 0~1
• Sign : -1 or 1
• tanh : 확장된 시그모이드. 중심값 0. -1 ~ 1
• ReLU : MAX(입력값, 0)
• SOftmax : 표준화지수함수. 출력값이 다범주일 때 사용. 범주에 속할 확률값 반환. 입력값 0~1사이로 만들어줌. 총합은 1

인공신경망 계층구조

• 단층신경망 (단층 퍼셉트론) : 입력층, 출력층
  • 출력값 : 임계값 넘으면 1 못넘으면 0
• 다층신경망 (다층 퍼셉트론) : 입력층, (다 수 의 은 닉 층), 출력층
  • 보통 인공신경망하면 다층신경망임.
  • 은닉층 노드 많다고 좋은거 아님. 너무많으면 과적합, 너무 적으면 과소적합. 적절한 수 찾아야됨.

역전파 알고리즘 (인공신경망 학습방법)

• 가중치값의 결정을 위해
  • 일단 가중치 만들기 : 순전파 알고리즘 활용 (입력층->출력층)
  • 거꾸로 오면서 오차 줄이기 : 역전파 알고리즘 활용 (출력층->입력층)
• 즉, 인공신경망이 학습한다 = 훈련용 데이터 넣어서 순전파, 역전파를 거쳐 가중치가 새롭게 조정되는 것. 학습 한 번은 1 epoch라고 함.
• 언제까지 학습함? : 일정 수 epoch에 도달하거나 만족스런 수준의 정확도 얻을 때 까지.

나비브베이즈 분류

사전지식. 베이즈 확률이 뭐임?

통계학 확률의 두 가지 구분

• 빈도확률(객관적 해석) : 사건발생 횟수의 장기적 비율. 근본적 반복.
• 베이지안 확률(주관적 해석) : 사전확률, 우도확률 -> 사후확률 추정. (즉, 데이터뿐 아니라 사람의 사전지식까지 동원해서 분석)

베이즈 정리의 확률 = 주장 Or 믿음의 신뢰도.

$P(H|E) = \frac{P(E|H)P(H)}{P(E)}$

나이브 베이즈 분류 모델 개념

베이즈정리 기반의 Supervised 모델.
가정 : 데이터의 모든 특징변수 동등, 독립적. 결과에 모두 독립적 기여.
활용 : 스팸메일 필터링, 텍스트 분류

나비브 베이즈 알고리즘

이진분류 데이터 입력 -> 베이즈이론 -> 범주 A, B가 될 확률 획득 -> 더 높은 확률의 범주에 데이터 할당

그러니까, 입력 주어지면, MAX(A일 확률, B일 확률)을 결과로 뱉는다.

각 범주에 속할 확률은 베이즈정리 확률 함수에 E=A, E=B만 하면 된다.
범주 A에 속할 확률 = P(A|E)
범주 B에 속할 확률 = P(B|E)

K-NN알고리즘

지도학습(분류학습)인데 비지도학습(군집특성)도 가짐.
-> 준 지도학습 이라고 말해도 됨

대충 하는 일 : 정답라벨 있는 데이터들 사이에, 지금 정답라벨 없는 데이터를 넣으면, 이거 어디로 가야되냐?

주변 K개 데이터(군집 잡기)의 평균으로 결정.
즉, 지도학습을 위한 정답으로 군집을 던져주는데, 군집은 비지도학습에 가깝다.

함수가 지역적으로 근사. 인스턴스 기반 학습 --> 게으른 학습.

서포트벡터머신 SVM

지도학습에 주로 사용. 분류성능 좋음->분류분석에 자주사용
초평면으로 카테고리를 분류 - 비확률적 이진 선형모델 생성

알고리즘

• 가장높은 바진을 가져가는 방향으로 분류. (마진이 크다 -> 처음보는 데이터 들어와도 분류 잘할 가능성 높음)
  • 이러니까 분류성능이 좋다. 그러니 분류분석에 많이 쓰지.

SVM구성

• 초평면, 초평면 집합으로 구성. (초평면은 분류분석, 회귀분석에 사용가능)
• 어떤 분류된 점에 대해, 가장 가까운 학습데이터와 가장 멀리있는 초평면 찾기. -> 오차 최소화

분류모형 성과평가

오분류표(혼동행렬, Confusion matrix)

테스트 데이터로부터 얻은 예측값, 실제값의 차이를 교차표 형태로 정리한 것.
훈

네 가지 분류

• TP : 예측값 T 실제값 T
• TN : 예측값 F 실제값 F
• FP : 예측값 T 실제값 F
• FN : 예측값 F 실제값 T

평가지표

• 정분류율(정확도) = (TP+TN) / 전체 : 잘한 비율
• 오분류율 = (FP+FN) / 전체 : 잘못한 비율
• 재현율(민감도, recall) = TP / (TP+FN) : 실제T 대비 예측T
• 특이도(specificity) = TN / (TN+FP) : 실제F 대비 예측F
• 정밀도(Precision) = TP / (TP+FP) : 예측T중 맞는 비율
• 거짓긍정률(FPR) = FP / (FP+TN) : 실제F인데 예측T로 한 경우.
• F1-Score = (2*정밀도*재현율) / (정밀도+재현율)

ROC커브

Epi library
ROC ( form=실제~예측, testdata, plot='ROC')

분류분석 모형 평가 쉽게 비교하기 위한 그래프. 시각화.
X축 FRP(실제F인데 예측T), Y축 TPR(민감도)
이진분류모형 평가.

AUROC = ROC커브 아래 면적

• 1에 가깝다 : 좋다
• 0.5에 가깝다 : 나쁘다. (무작위예측 랜덤모델에 가깝다)

이익도표

= 이득곡선, 이득도표.

목표범주에 속할 확률 내림차순 정렬.
구간 나눠서 각 구간 성능파단. 랜덤모델보다 얼마나 성능 좋냐 확인.

0.5에서 cut-off. 1.0이 제일 좋음.

향상도곡선

Lift Curve

랜덤모델 대비 해당 모델 성과가 얼마나 향상됐냐?
좋은모델 : 큰값에서 시작, 급격히 감소

ROCR Library
plot( performance(lift_value, 'lift', 'rpp') )
Y축 향상정도
x축 긍정예측.

군집분석(Clustering)

군집분석 일반

활용 : 생물 종의 분류, 마케팅 시장세분화, 산업분석, 협업필터링.

거리측도 : 관측치 유사성 측정을 위한 방법

• 연속형 변수
  • 맨하탄거리, 유클리디안거리, 체비세프거리 : 지수 1 2 3
    • 유클리디안 거리 주의 : 단위 다를 수 있으니, 정규화, 표준화 수행
  • 표준화거리, 마할라노비스 : 지수 1/2, 각각 성분이 분산(D행렬), 공분산(S행렬)
  • 민코프스키 거리 : 지수 1/m. -> m=1이면 맨하탄, m=2이면 유클리디안.
• 범주형 변수 : 얼마나 많은 공통요소를 갖고있나?
  • 단순일치계수(SMC) : m/p=같은 수/전체 수 (두 객체간의 상이성을 불일치비율로 계산)
  • 자카드지수 : 두 집합 유사도 측정. 같으면 1, 다르면 0
  • 자카드거리 : 자카드지수의 거리화. 1-자카드지수 (다르면 가장 먼 거리 = 1)
  • 코사인유사도 : 텍스트 유사도(방향성)측정. 완전일치 1, 완전다름 -1
  • 코사인거리 : 1-코사인유사도
  • 순위상관계수 : 순서척도 데이터 사이 거리 측정. 스피어만 상관계수.

실루엣계수 : 군집분석 평가지표. 응집도, 분리도 계산. 1에 가까우면 완벽분리.

계층적 군집분석

hclust( 거리 데이터, method )

개별 간측치간 거리 계산.
가까운 관측치부터 결합. -> 계층적 트리구조 형성. -> 군집화 수행.
덴드로그램으로 계층구조 시각화

계층적 군집 방법

• 병합적방법(묶기) : 데이터 각각이 군집 -> 순차적으로 결합. -> 군집수 감소
  • 몇개로 묶을건지 미리 안정해도 됨. 결과 뜨는거 보고 적당히 설명가능한 수준으로 군집 수 정하면 됨.
• 분할적방법(나누기) : 전체 데이터 통째로를 군집으로 간주(군집 1개) -> 분할 -> 군집수 증가.

군집 간 거리

• 단일연결법(최단연결법) : 군집간 가까운 것 끼리 거리 잰다 single
• 완전연결법 : 군집간 젤 먼거끼리 거리 잰다 complete
• 평균연결법 : 모든 거리 경우의 수 싹다재서 평균냄. average
• 중심연결법 : 각 군집 중심끼리 거리 잼
• 와드연결법 : 군집 내 오차를 최소화하는 데이터로 계산. - 군집내 분산 최소화->조밀한 군집. 비슷한 크기의 군집끼리 병합하는 경향.

비계층적 군집분석

군집수 사전 정의 . 그 수만큼 군집 형성.
데이터간 거리행렬 사용 안함.

k-mean 군집 flexclust Nclus kmeans

• 군집수 k개 정하고, 집단내 동질성, 집단간 이질성 커지게 k개 군집 만듦.
• 임의로 설정된 초기 k개 데이터 = seed
• 단순하고 빠름. 다양한 데이터 사용 가능. (물론 연속형이라면)
• 연속형 변수. 안정군집 보장하지만 최적이 아닐수도. 이상값에 민감(평균값대신 중앙값 사용으로 해결볼수있음). 결과해석 어려움.

집단내 제곱합 그래프
k-mean 군집의 초기k값 설정편의를 위한 그래프.
k값을 1부터 차레로 늘려가며 k-mean을 돌렸을 때, 군집내 데이터들ㅡ군집중심 거리의 제곱합.
군집수 증가->제곱합 작아짐. 어느 k시점부터 감소량 급감.

K-medoids : k-mean군집의 이상값에 대한 민감함을보완.

• 차이점 : 시드값은 데이터중에 선택. 시드 이동은 해당클러스터에 속한 데이터중에서 다른 데ㅣ터와 거리가 최소화되는 것으로 고름.
• 요약 : 시드 정하는데 낭비 큼. 시간 오래걸림.
• 그러나 좋은점 상기 : 이상값에 민감하지 않음.

DBSCAN fpc dbscan dbscan$cluster
개체간 거리가 아니라, 밀도기반으로 군집분석.
데이터 분포 기하학적이고 노이즈 있어도 군집 잘 만듦.
초기군집 수 안정해도 됨.

혼합분포군집

같은 확률분포에서 추출된 데이터끼리 군집화.
확률분포 모수, 비중을 찾는 것이 목적.

모수, 가중치 추정 방법 : EM(기댓값 최대화) normalmixEM

• 두 가지 단계. E, M.

SOM 자기조직화지도

kohonen

코호넨 맵. 인공신경망 기반 차원축소, 군집화 -> 동시수행.

입력공간 속성 보존.
고차원데이터를 2차원공간에 정렬 시각화 -> 보기쉽다

구성
은닉층 없다. 입력층. 경쟁층.
입력층과 경쟁층 모든노드 완전연결.
유클리디안거리비교.
결국 경쟁층의 가장 가까운 하나의 노드에 최종적으로 도달 = 승자노드.

특징
역전파 안함. 순전파만. -> 빨라.
보기쉽다. 패턴발견, 이미지분석 잘함. 입력데이터 속성 보존.
그러나 초기학습률, 가중치에 영향 많이받음. 경쟁층 노드 개수 결정하기 어려움.

연관분석(Association Analysis)

개요, 측도

알고리즘, 특징.