제곱수의 합

문제

어떤 자연수 N은 그보다 작거나 같은 제곱수들의 합으로 나타낼 수 있다. 예를 들어 11=32+12+12(3개 항)이다. 이런 표현방법은 여러 가지가 될 수 있는데, 11의 경우 11=22+22+12+12+12(5개 항)도 가능하다. 이 경우, 수학자 숌크라테스는 “11은 3개 항의 제곱수 합으로 표현할 수 있다.”라고 말한다. 또한 11은 그보다 적은 항의 제곱수 합으로 표현할 수 없으므로, 11을 그 합으로써 표현할 수 있는 제곱수 항의 최소 개수는 3이다.

주어진 자연수 N을 이렇게 제곱수들의 합으로 표현할 때에 그 항의 최소개수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 100,000)

출력

주어진 자연수를 제곱수의 합으로 나타낼 때에 그 제곱수 항의 최소 개수를 출력한다.

---

풀이

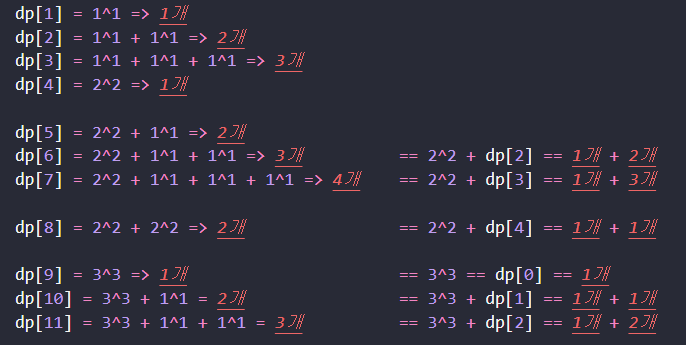
위 규칙을 통해

자연수 N보다 작은 제곱수 항 (1개) + dp[자연수 N - 제곱수]의 개수가 최소가 되는 경우가 dp[N]을 만족한다는 것을 알 수 있다!

여기서 자연수 N과 가장 가까운 제곱수 즉, N보다 작은 가장 큰 제곱수를 기준으로 최소 개수를 만족할 수 있지 않을까? 하는 의구심이 들었다.

그러나, 아래와 같은 반례가 존재했다.

9는 12보다 작은, 가장 큰 제곱수이지만 12에서 9를 뺀 dp[3]에서 최소 제곱수의 항이 3개 이다.
4는 12보다 작은, 가장 큰 제곱수는 아니지만 12에서 4를 뺀 dp[8]에서 최소 제곱수의 항이 2개이므로 dp[12]의 최소 제곱수 개수는 3개가 된다.

따라서, 최선의 방법은
"N보다 작은 제곱수를 뺀 dp[N-제곱수]의 값 + 1 (자연수 N보다 작은 제곱수의 항)"의 min값을 찾는 것이다.

코드

n = int(input())

# 최솟값을 찾아야하기 때문에 0으로 초기화 불가! 
dp = [i for i in range(n+1)] 

for i in range(4, n+1):
    for j in range(1,i):
        
        if j*j > i:
            break

        if dp[i] > dp[i-(j*j)] +1:
            dp[i] = dp[i-(j*j)] +1

후기

• dp는 아직도 어렵다 ㅠ